Apollonian network


In combinatorial mathematics, an Apollonian network is an undirected graph formed by a process of recursively subdividing a triangle into three smaller triangles. Apollonian networks may equivalently be defined as the planar 3-trees, the maximal planar chordal graphs, the uniquely 4-colorable planar graphs, and the graphs of stacked polytopes. They are named after Apollonius of Perga, who studied a related circle-packing construction.
Definition[]
An Apollonian network may be formed, starting from a single triangle embedded in the Euclidean plane, by repeatedly selecting a triangular face of the embedding, adding a new vertex inside the face, and connecting the new vertex to each vertex of the face containing it. In this way, the triangle containing the new vertex is subdivided into three smaller triangles, which may in turn be subdivided in the same way.
Examples[]
The complete graphs on three and four vertices, K3 and K4, are both Apollonian networks. K3 is formed by starting with a triangle and not performing any subdivisions, while K4 is formed by making a single subdivision before stopping.
The Goldner–Harary graph is an Apollonian network that forms the smallest non-Hamiltonian maximal planar graph.[1] Another more complicated Apollonian network was used by Nishizeki (1980) to provide an example of a 1-tough non-Hamiltonian maximal planar graph.
Graph-theoretic characterizations[]
As well as being defined by recursive subdivision of triangles, the Apollonian networks have several other equivalent mathematical characterizations. They are the chordal maximal planar graphs, the chordal polyhedral graphs, and the planar 3-trees. They are the uniquely 4-colorable planar graphs, and the planar graphs with a unique Schnyder wood decomposition into three trees. They are the maximal planar graphs with treewidth three, a class of graphs that can be characterized by their forbidden minors or by their reducibility under Y-Δ transforms. They are the maximal planar graphs with degeneracy three. They are also the planar graphs on a given number of vertices that have the largest possible number of triangles, the largest possible number of tetrahedral subgraphs, the largest possible number of cliques, and the largest possible number of pieces after decomposing by separating triangles.
Chordality[]
Apollonian networks are examples of maximal planar graphs, graphs to which no additional edges can be added without destroying planarity, or equivalently graphs that can be drawn in the plane so that every face (including the outer face) is a triangle. They are also chordal graphs, graphs in which every cycle of four or more vertices has a diagonal edge connecting two non-consecutive cycle vertices, and the order in which vertices are added in the subdivision process that forms an Apollonian network is an elimination ordering as a chordal graph. This forms an alternative characterization of the Apollonian networks: they are exactly the chordal maximal planar graphs or equivalently the chordal polyhedral graphs.[2]
In an Apollonian network, every maximal clique is a complete graph on four vertices, formed by choosing any vertex and its three earlier neighbors. Every minimal clique separator (a clique that partitions the graph into two disconnected subgraphs) is one of the subdivided triangles. A chordal graph in which all maximal cliques and all minimal clique separators have the same size is a k-tree, and Apollonian networks are examples of 3-trees. Not every 3-tree is planar, but the planar 3-trees are exactly the Apollonian networks.
Unique colorability[]
Every Apollonian network is also a uniquely 4-colorable graph. Because it is a planar graph, the four color theorem implies that it has a graph coloring with only four colors, but once the three colors of the initial triangle are selected, there is only one possible choice for the color of each successive vertex, so up to permutation of the set of colors it has exactly one 4-coloring. It is more difficult to prove, but also true, that every uniquely 4-colorable planar graph is an Apollonian network. Therefore, Apollonian networks may also be characterized as the uniquely 4-colorable planar graphs.[3] Apollonian networks also provide examples of planar graphs having as few k-colorings as possible for k > 4.[4]
The Apollonian networks are also exactly the maximal planar graphs that (once an exterior face is fixed) have a unique Schnyder wood, a partition of the edges of the graph into three interleaved trees rooted at the three vertices of the exterior face.[5]
Treewidth[]
The Apollonian networks do not form a family of graphs that is closed under the operation of taking graph minors, as removing edges but not vertices from an Apollonian network produces a graph that is not an Apollonian network. However, the planar partial 3-trees, subgraphs of Apollonian networks, are minor-closed. Therefore, according to the Robertson–Seymour theorem, they can be characterized by a finite number of forbidden minors. The minimal forbidden minors for the planar partial 3-trees are the four minimal graphs among the forbidden minors for the planar graphs and the partial 3-trees: the complete graph K5, the complete bipartite graph K3,3, the graph of the octahedron, and the graph of the pentagonal prism. The Apollonian graphs are the maximal graphs that do not have any of these four graphs as a minor.[6]
A Y-Δ transform, an operation that replaces a degree-three vertex in a graph by a triangle connecting its neighbors, is sufficient (together with the removal of parallel edges) to reduce any Apollonian network to a single triangle, and more generally the planar graphs that can be reduced to a single edge by Y-Δ transforms, removal of parallel edges, removal of degree-one vertices, and compression of degree-two vertices are exactly the planar partial 3-trees. The dual graphs of the planar partial 3-trees form another minor-closed graph family and are exactly the planar graphs that can be reduced to a single edge by Δ-Y transforms, removal of parallel edges, removal of degree-one vertices, and compression of degree-two vertices.[7]
Degeneracy[]
In every subgraph of an Apollonian network, the most recently added vertex has degree at most three, so Apollonian networks have degeneracy three. The order in which the vertices are added to create the network is therefore a degeneracy ordering, and the Apollonian networks coincide with the 3-degenerate maximal planar graphs.
Extremality[]
Another characterization of the Apollonian networks involves their connectivity. Any maximal planar graph may be decomposed into 4-vertex-connected maximal planar subgraphs by splitting it along its separating triangles (triangles that are not faces of the graph): given any non-facial triangle: one can form two smaller maximal planar graphs, one consisting of the part inside the triangle and the other consisting of the part outside the triangle. The maximal planar graphs without separating triangles that may be formed by repeated splits of this type are sometimes called blocks, although that name has also been used for the biconnected components of a graph that is not itself biconnected. An Apollonian network is a maximal planar graph in which all of the blocks are isomorphic to the complete graph K4.
In extremal graph theory, Apollonian networks are also exactly the n-vertex planar graphs in which the number of blocks achieves its maximum, n − 3, and the planar graphs in which the number of triangles achieves its maximum, 3n − 8. Since each K4 subgraph of a planar graph must be a block, these are also the planar graphs in which the number of K4 subgraphs achieves its maximum, n − 3, and the graphs in which the number of cliques of any type achieves its maximum, 8n − 16.[8]
Geometric realizations[]
Construction from circle packings[]
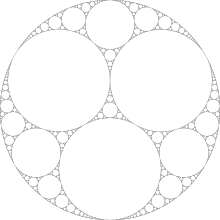

Apollonian networks are named after Apollonius of Perga, who studied the Problem of Apollonius of constructing a circle tangent to three other circles. One method of constructing Apollonian networks is to start with three mutually-tangent circles and then repeatedly inscribe another circle within the gap formed by three previously-drawn circles. The fractal collection of circles produced in this way is called an Apollonian gasket.
If the process of producing an Apollonian gasket is stopped early, with only a finite set of circles, then the graph that has one vertex for each circle and one edge for each pair of tangent circles is an Apollonian network.[9] The existence of a set of tangent circles whose tangencies represent a given Apollonian network forms a simple instance of the Koebe–Andreev–Thurston circle-packing theorem, which states that any planar graph can be represented by tangent circles in the same way.[10]
Polyhedra[]

Apollonian networks are planar 3-connected graphs and therefore, by Steinitz's theorem, can always be represented as the graphs of convex polyhedra. The convex polyhedron representing an Apollonian network is a 3-dimensional stacked polytope. Such a polytope can be obtained from a tetrahedron by repeatedly gluing additional tetrahedra one at a time onto its triangular faces. Therefore, Apollonian networks may also be defined as the graphs of stacked 3d polytopes.[11] It is possible to find a representation of any Apollonian network as convex 3d polyhedron in which all of the coordinates are integers of polynomial size, better than what is known for other planar graphs.[12]
Triangle meshes[]
The recursive subdivision of triangles into three smaller triangles was investigated as an image segmentation technique in computer vision by Elcock, Gargantini & Walsh (1987); in this context, they called it the ternary scalene triangle decomposition. They observed that, by placing each new vertex at the centroid of its enclosing triangle, the triangulation could be chosen in such a way that all triangles have equal areas, although they do not all have the same shape. More generally, Apollonian networks may be drawn in the plane with any prescribed area in each face; if the areas are rational numbers, so are all of the vertex coordinates.[13]
It is also possible to carry out the process of subdividing a triangle to form an Apollonian network in such a way that, at every step, the edge lengths are rational numbers; it is an open problem whether every planar graph has a drawing with this property.[14] It is possible in polynomial time to find a drawing of a planar 3-tree with integer coordinates minimizing the area of the bounding box of the drawing, and to test whether a given planar 3-tree may be drawn with its vertices on a given set of points.[15]
Properties and applications[]
Matching-free graphs[]
Plummer (1992) used Apollonian networks to construct an infinite family of maximal planar graphs with an even number of vertices but with no perfect matching. Plummer's graphs are formed in two stages. In the first stage, starting from a triangle abc, one repeatedly subdivides the triangular face of the subdivision that contains edge bc: the result is a graph consisting of a path from a to the final subdivision vertex together with an edge from each path vertex to each of b and c. In the second stage, each of the triangular faces of the resulting planar graph is subdivided one more time. If the path from a to the final subdivision vertex of the first stage has even length, then the number of vertices in the overall graph is also even. However, approximately 2/3 of the vertices are the ones inserted in the second stage; these form an independent set, and cannot be matched to each other, nor are there enough vertices outside the independent set to find matches for all of them.
Although Apollonian networks themselves may not have perfect matchings, the planar dual graphs of Apollonian networks are 3-regular graphs with no cut edges, so by a theorem of Petersen (1891) they are guaranteed to have at least one perfect matching. However, in this case more is known: the duals of Apollonian networks always have an exponential number of perfect matchings.[16] László Lovász and Michael D. Plummer conjectured that a similar exponential lower bound holds more generally for every 3-regular graph without cut edges, a result that was later proven.
Power law graphs[]
Andrade et al. (2005) studied power laws in the degree sequences of a special case of networks of this type, formed by subdividing all triangles the same number of times. They used these networks to model packings of space by particles of varying sizes. Based on their work, other authors introduced random Apollonian networks, formed by repeatedly choosing a random face to subdivide, and they showed that these also obey power laws in their degree distribution [17] and have small average distances.[18] Alan M. Frieze and Charalampos E. Tsourakakis analyzed the highest degrees and the eigenvalues of random Apollonian networks.[19] Andrade et al. also observed that their networks satisfy the small world effect, that all vertices are within a small distance of each other. Based on numerical evidence they estimated the average distance between randomly selected pairs of vertices in an n-vertex network of this type to be proportional to (log n)3/4, but later researchers showed that the average distance is actually proportional to log n.[20]
Angle distribution[]
Butler & Graham (2010) observed that if each new vertex is placed at the incenter of its triangle, so that the edges to the new vertex bisect the angles of the triangle, then the set of triples of angles of triangles in the subdivision, when reinterpreted as triples of barycentric coordinates of points in an equilateral triangle, converges in shape to the Sierpinski triangle as the number of levels of subdivision grows.
Hamiltonicity[]
Takeo (1960) claimed erroneously that all Apollonian networks have Hamiltonian cycles; however, the Goldner–Harary graph provides a counterexample. If an Apollonian network has toughness greater than one (meaning that removing any set of vertices from the graph leaves a smaller number of connected components than the number of removed vertices) then it necessarily has a Hamiltonian cycle, but there exist non-Hamiltonian Apollonian networks whose toughness is equal to one.[21]
Enumeration[]
The combinatorial enumeration problem of counting Apollonian triangulations was studied by Takeo (1960), who showed that they have the simple generating function f(x) described by the equation f(x) = 1 + x(f(x))3. In this generating function, the term of degree n counts the number of Apollonian networks with a fixed outer triangle and n + 3 vertices. Thus, the numbers of Apollonian networks (with a fixed outer triangle) on 3, 4, 5, ... vertices are:
a sequence that also counts ternary trees and dissections of convex polygons into odd-sided polygons. For instance, there are 12 6-vertex Apollonian networks: three formed by subdividing the outer triangle once and then subdividing two of the resulting triangles, and nine formed by subdividing the outer triangle once, subdividing one of its triangles, and then subdividing one of the resulting smaller triangles.
History[]
Birkhoff (1930) is an early paper that uses a dual form of Apollonian networks, the planar maps formed by repeatedly placing new regions at the vertices of simpler maps, as a class of examples of planar maps with few colorings.
Geometric structures closely related to Apollonian networks have been studied in polyhedral combinatorics since at least the early 1960s, when they were used by Grünbaum (1963) to describe graphs that can be realized as the graph of a polytope in only one way, without dimensional or combinatorial ambiguities, and by Moon & Moser (1963) to find simplicial polytopes with no long paths. In graph theory, the close connection between planarity and treewidth goes back to Robertson & Seymour (1984), who showed that every minor-closed family of graphs either has bounded treewidth or contains all of the planar graphs. Planar 3-trees, as a class of graphs, were explicitly considered by Hakimi & Schmeichel (1979), Alon & Caro (1984), Patil (1986), and many authors since them.
The name "Apollonian network" was given by Andrade et al. (2005) to the networks they studied in which the level of subdivision of triangles is uniform across the network; these networks correspond geometrically to a type of stacked polyhedron called a Kleetope.[22] Other authors applied the same name more broadly to planar 3-trees in their work generalizing the model of Andrade et al. to random Apollonian networks.[18] The triangulations generated in this way have also been named "stacked triangulations"[23] or "stack-triangulations".[24]
See also[]
- Barycentric subdivision, a different method of subdividing triangles into smaller triangles
- Loop subdivision surface, yet another method of subdividing triangles into smaller triangles
Notes[]
- ^ This graph is named after the work of Goldner & Harary (1975); however, it appears earlier in the literature, for instance in Grünbaum (1967), p. 357.
- ^ The equivalence of planar 3-trees and chordal maximal planar graphs was stated without proof by Patil (1986). For a proof, see Markenzon, Justel & Paciornik (2006). For a more general characterization of chordal planar graphs, and an efficient recognition algorithm for these graphs, see Kumar & Madhavan (1989). The observation that every chordal polyhedral graph is maximal planar was stated explicitly by Gerlach (2004).
- ^ Fowler (1998).
- ^ The fact that Apollonian networks minimize the number of colorings with more than four of colors was shown in a dual form for colorings of maps by Birkhoff (1930).
- ^ Felsner & Zickfeld (2008); Bernardi & Bonichon (2009).
- ^ The two forbidden minors for planar graphs are given by Wagner's theorem. For the forbidden minors for partial 3-trees (which include also the nonplanar Wagner graph) see Arnborg, Proskurowski & Corniel (1986) and Bodlaender (1998). For direct proofs that the octahedral graph and the pentagonal-prism graph are the only two planar forbidden minors, see Dai & Sato (1990) and El-Mallah & Colbourn (1990).
- ^ Politof (1983) introduced the Δ-Y reducible planar graphs and characterized them in terms of forbidden homeomorphic subgraphs. The duality between the Δ-Y and Y-Δ reducible graphs, the forbidden minor characterizations of both classes, and the connection to planar partial 3-trees are all from El-Mallah & Colbourn (1990).
- ^ For the characterization in terms of the maximum number of triangles in a planar graph, see Hakimi & Schmeichel (1979). Alon & Caro (1984) quote this result and provide the characterizations in terms of the isomorphism classes of blocks and numbers of blocks. The bound on the total number of cliques follows easily from the bounds on triangles and K4 subgraphs, and is also stated explicitly by Wood (2007), who provides an Apollonian network as an example showing that this bound is tight. For generalizations of these bounds to nonplanar surfaces, see Dujmović et al. (2009).
- ^ Andrade et al. (2005).
- ^ Thurston (1978–1981).
- ^ See, e.g., Below, De Loera & Richter-Gebert (2000).
- ^ Demaine & Schulz (2011).
- ^ Biedl & Ruiz Velázquez (2010).
- ^ For subdividing a triangle with rational side lengths so that the smaller triangles also have rational side lengths, see Almering (1963). For progress on the general problem of finding planar drawings with rational edge lengths, see Geelen, Guo & McKinnon (2008).
- ^ For the drawings with integer coordinates, see Mondal et al. (2010), and for the drawings on a given vertex set, see Nishat, Mondal & Rahman (2011).
- ^ Jiménez & Kiwi (2010).
- ^ Tsourakakis (2011)
- ^ a b Zhou et al. (2004); Zhou, Yan & Wang (2005).
- ^ Frieze & Tsourakakis (2011)
- ^ Albenque & Marckert (2008);Zhang et al. (2008).
- ^ See Nishizeki (1980) for a 1-tough non-Hamiltonian example, Böhme, Harant & Tkáč (1999) for the proof that Apollonian networks with greater toughness are Hamiltonian, and Gerlach (2004) for an extension of this result to a wider class of planar graphs.
- ^ Grünbaum (1963); Grünbaum (1967).
- ^ Alon & Caro (1984); Zickfeld & Ziegler (2006); Badent et al. (2007); Felsner & Zickfeld (2008).
- ^ Albenque & Marckert (2008); Bernardi & Bonichon (2009); Jiménez & Kiwi (2010).
References[]
- Albenque, Marie; Marckert, Jean-François (2008), "Some families of increasing planar maps", Electronic Journal of Probability, 13: 1624–1671, arXiv:0712.0593, doi:10.1214/ejp.v13-563, MR 2438817, S2CID 2420262
- Almering, J. H. J. (1963), "Rational quadrilaterals", Indagationes Mathematicae, 25: 192–199, doi:10.1016/S1385-7258(63)50020-1, MR 0147447.
- Alon, N.; Caro, Y. (1984), "On the number of subgraphs of prescribed type of planar graphs with a given number of vertices", in Rosenfeld, M.; Zaks, J. (eds.), Convexity and Graph Theory: proceedings of the Conference on Convexity and Graph Theory, Israel, March 1981, Annals of Discrete Mathematics 20, North-Holland Mathematical Studies 87, Elsevier, pp. 25–36, ISBN 978-0-444-86571-7, MR 0791009.
- Andrade, José S., Jr.; Herrmann, Hans J.; Andrade, Roberto F. S.; da Silva, Luciano R. (2005), "Apollonian Networks: Simultaneously Scale-Free, Small World, Euclidean, Space Filling, and with Matching Graphs", Physical Review Letters, 94 (1): 018702, arXiv:cond-mat/0406295, Bibcode:2005PhRvL..94a8702A, doi:10.1103/physrevlett.94.018702, PMID 15698147.
- Arnborg, S.; Proskurowski, A.; Corniel, D. (1986), Forbidden Minors Characterization of Partial 3-trees, Technical Report CIS-TR-86-07, Dept. of Computer and Information Science, University of Oregon. As cited by El-Mallah & Colbourn (1990).
- Badent, Melanie; Binucci, Carla; Di Giacomo, Emilio; Didimo, Walter; Felsner, Stefan; Giordano, Francesco; Kratochvíl, Jan; Palladino, Pietro; Patrignani, Maurizio; Trotta, Francesco (2007), "Homothetic triangle contact representations of planar graphs", Canadian Conference on Computational Geometry (PDF).
- Below, Alexander; De Loera, Jesús A.; Richter-Gebert, Jürgen (2000), The Complexity of Finding Small Triangulations of Convex 3-Polytopes, arXiv:math/0012177, Bibcode:2000math.....12177B.
- Bernardi, Olivier; Bonichon, Nicolas (2009), "Intervals in Catalan lattices and realizers of triangulations", Journal of Combinatorial Theory, Series A, 116 (1): 55–75, doi:10.1016/j.jcta.2008.05.005, MR 2469248.
- Biedl, Therese; Ruiz Velázquez, Lesvia Elena (2010), "Drawing planar 3-trees with given face-areas", Graph Drawing, 17th International Symposium, GD 2009, Chicago, IL, USA, September 22–25, 2009, Revised Papers, Lecture Notes in Computer Science, vol. 5849, Springer-Verlag, pp. 316–322, doi:10.1007/978-3-642-11805-0_30.
- Birkhoff, George D. (1930), "On the number of ways of colouring a map", Proceedings of the Edinburgh Mathematical Society, (2), 2 (2): 83–91, doi:10.1017/S0013091500007598.
- Bodlaender, Hans L. (1998), "A partial k-arboretum of graphs with bounded treewidth", Theoretical Computer Science, 209 (1–2): 1–45, doi:10.1016/S0304-3975(97)00228-4, hdl:1874/18312, MR 1647486.
- Böhme, Thomas; Harant, Jochen; Tkáč, Michal (1999), "More than one tough chordal planar graphs are Hamiltonian", Journal of Graph Theory, 32 (4): 405–410, doi:10.1002/(SICI)1097-0118(199912)32:4<405::AID-JGT8>3.3.CO;2-Q, MR 1722793.
- Butler, S.; Graham, Ron (2010), "Iterated triangle partitions", in Katona, G.; Schrijver, A.; Szonyi, T. (eds.), Fete of Combinatorics and Computer Science (PDF), Bolyai Society Mathematical Studies, vol. 29, Heidelberg: Springer-Verlag, pp. 23–42.
- Dai, Wayne Wei-Ming; Sato, Masao (1990), "Minimal forbidden minor characterization of planar partial 3-trees and application to circuit layout", IEEE International Symposium on Circuits and Systems, vol. 4, pp. 2677–2681, doi:10.1109/ISCAS.1990.112560, S2CID 122926229
- Demaine, Erik; Schulz, André (2011), "Embedding stacked polytopes on a polynomial-size grid", Proc. ACM-SIAM Symposium on Discrete Algorithms (PDF), pp. 1177–1187, archived from the original (PDF) on 2011-06-01, retrieved 2011-03-07.
- Dujmović, Vida; Fijavž, Gašper; Joret, Gwenaël; Wood, David R. (2009), "The maximum number of cliques in a graph embedded in a surface", European Journal of Combinatorics, 32 (8): 1244–1252, arXiv:0906.4142, Bibcode:2009arXiv0906.4142D, doi:10.1016/j.ejc.2011.04.001, S2CID 1733300.
- El-Mallah, Ehab S.; Colbourn, Charles J. (1990), "On two dual classes of planar graphs", Discrete Mathematics, 80 (1): 21–40, doi:10.1016/0012-365X(90)90293-Q, MR 1045921.
- Elcock, E. W.; Gargantini, I.; Walsh, T. R. (1987), "Triangular decomposition", Image and Vision Computing, 5 (3): 225–231, doi:10.1016/0262-8856(87)90053-9.
- Felsner, Stefan; Zickfeld, Florian (2008), "On the number of planar orientations with prescribed degrees" (PDF), Electronic Journal of Combinatorics, 15 (1): R77, arXiv:math/0701771, Bibcode:2007math......1771F, doi:10.37236/801, MR 2411454, S2CID 13893657.
- Frieze, Alan M.; Tsourakakis, Charalampos E. (2011), High Degree Vertices, Eigenvalues and Diameter of Random Apollonian Networks, arXiv:1104.5259, Bibcode:2011arXiv1104.5259F.
- Fowler, Thomas (1998), Unique Coloring of Planar Graphs (PDF), Ph.D. thesis, Georgia Institute of Technology Mathematics Department.
- Geelen, Jim; Guo, Anjie; McKinnon, David (2008), "Straight line embeddings of cubic planar graphs with integer edge lengths", Journal of Graph Theory, 58 (3): 270–274, doi:10.1002/jgt.20304, MR 2419522.
- Gerlach, T. (2004), "Toughness and Hamiltonicity of a class of planar graphs", Discrete Mathematics, 286 (1–2): 61–65, doi:10.1016/j.disc.2003.11.046, MR 2084280.
- Goldner, A.; Harary, F. (1975), "Note on a smallest nonhamiltonian maximal planar graph", Bull. Malaysian Math. Soc., 6 (1): 41–42. See also the same journal 6(2):33 (1975) and 8:104-106 (1977). Reference from listing of Harary's publications.
- Grünbaum, Branko (1963), "Unambiguous polyhedral graphs", Israel Journal of Mathematics, 1 (4): 235–238, doi:10.1007/BF02759726, MR 0185506, S2CID 121075042.
- Grünbaum, Branko (1967), Convex Polytopes, Wiley Interscience.
- Hakimi, S. L.; Schmeichel, E. F. (1979), "On the number of cycles of length k in a maximal planar graph", Journal of Graph Theory, 3 (1): 69–86, doi:10.1002/jgt.3190030108, MR 0519175.
- Jiménez, Andrea; Kiwi, Marcos (2010), Counting perfect matchings of cubic graphs in the geometric dual, arXiv:1010.5918, Bibcode:2010arXiv1010.5918J.
- Kumar, P. Sreenivasa; Madhavan, C. E. Veni (1989), "A new class of separators and planarity of chordal graphs", Foundations of Software Technology and Theoretical Computer Science, Ninth Conference, Bangalore, India December 19–21, 1989, Proceedings, Lecture Notes in Computer Science, vol. 405, Springer-Verlag, pp. 30–43, doi:10.1007/3-540-52048-1_30, MR 1048636.
- Markenzon, L.; Justel, C. M.; Paciornik, N. (2006), "Subclasses of k-trees: Characterization and recognition", Discrete Applied Mathematics, 154 (5): 818–825, doi:10.1016/j.dam.2005.05.021, MR 2207565.
- Mondal, Debajyoti; Nishat, Rahnuma Islam; Rahman, Md. Saidur; Alam, Muhammad Jawaherul (2010), "Minimum-area drawings of plane 3-trees", Canadian Conference on Computational Geometry (PDF).
- Moon, J. W.; Moser, L. (1963), "Simple paths on polyhedra", Pacific Journal of Mathematics, 13 (2): 629–631, doi:10.2140/pjm.1963.13.629, MR 0154276.
- Nishat, Rahnuma Islam; Mondal, Debajyoti; Rahman, Md. Saidur (2011), "Point-set embeddings of plane 3-trees", Graph Drawing, 18th International Symposium, GD 2010, Konstanz, Germany, September 21–24, 2010, Revised Selected Papers, Lecture Notes in Computer Science, vol. 6502, Springer-Verlag, pp. 317–328, doi:10.1007/978-3-642-18469-7_29.
- Nishizeki, Takao (1980), "A 1-tough non-Hamiltonian maximal planar graph", Discrete Mathematics, 30 (3): 305–307, doi:10.1016/0012-365X(80)90240-X, MR 0573648.
- Patil, H. P. (1986), "On the structure of k-trees", Journal of Combinatorics, Information and System Sciences, 11 (2–4): 57–64, MR 0966069.
- Petersen, Julius (1891), "Die Theorie der regulären graphs", Acta Mathematica, 15: 193–220, doi:10.1007/BF02392606.
- Plummer, Michael D. (1992), "Extending matchings in planar graphs IV", Discrete Mathematics, 109 (1–3): 207–219, doi:10.1016/0012-365X(92)90292-N, MR 1192384.
- Politof, T. (1983), A characterization and efficient reliability computation of Δ-Y reducible networks, Ph.D. thesis, University of California, Berkeley. As cited by El-Mallah & Colbourn (1990).
- Robertson, Neil; Seymour, P. D. (1984), "Graph minors. III. Planar tree-width", Journal of Combinatorial Theory, Series B, 36 (1): 49–64, doi:10.1016/0095-8956(84)90013-3, MR 0742386.
- Takeo, Fujio (1960), "On triangulated graphs. I", Bull. Fukuoka Gakugei Univ. III, 10: 9–21, MR 0131372. An error regarding Hamiltonicity was pointed out by MathSciNet reviewer W. T. Tutte.
- Thurston, William (1978–1981), The geometry and topology of 3-manifolds, Princeton lecture notes.
- Tsourakakis, Charalampos E. (2011), The Degree Sequence of Random Apollonian Networks, arXiv:1106.1940.
- Wood, David R. (2007), "On the maximum number of cliques in a graph", Graphs and Combinatorics, 23 (3): 337–352, arXiv:math/0602191, doi:10.1007/s00373-007-0738-8, MR 2320588, S2CID 46700417.
- Zhang, Zhongzhi; Chen, Lichao; Zhou, Shuigeng; Fang, Lujun; Guan, Jihong; Zou, Tao (2008), "Analytical solution of average path length for Apollonian networks", Physical Review E, 77 (1): 017102, arXiv:0706.3491, Bibcode:2008PhRvE..77a7102Z, doi:10.1103/PhysRevE.77.017102, PMID 18351964, S2CID 30404208.
- Zhou, Tao; Yan, Gang; Wang, Bing-Hong (2005), "Maximal planar networks with large clustering coefficient and power-law degree distribution", Physical Review E, 71 (4): 046141, arXiv:cond-mat/0412448, Bibcode:2005PhRvE..71d6141Z, doi:10.1103/PhysRevE.71.046141, PMID 15903760, S2CID 21740312.
- Zhou, Tao; Yan, Gang; Zhou, Pei-Ling; Fu, Zhong-Qian; Wang, Bing-Hong (2004), Random Apollonian networks, arXiv:cond-mat/0409414v2, Bibcode:2004cond.mat..9414Z.
- Zickfeld, Florian; Ziegler, Günter M. (2006), "Integer realizations of stacked polytopes", Workshop on Geometric and Topological Combinatorics (PDF).
External links[]
- Graph families
- Perfect graphs
- Planar graphs
- Triangulation (geometry)