Barometric formula

The barometric formula, sometimes called the exponential atmosphere or isothermal atmosphere, is a formula used to model how the pressure (or density) of the air changes with altitude. The pressure drops approximately by 11.3 pascals per meter in first 1000 meters above sea level.

Pressure equations[]

Pressure as a function of the height above the sea level

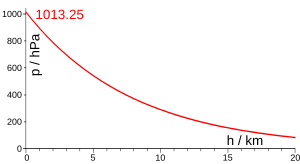
There are two different equations for computing pressure at various height regimes below 86 km (or 278,400 feet). The first equation is used when the value of standard temperature lapse rate is not equal to zero:

${\displaystyle {P}=P_{b}\cdot \left[{\frac {T_{b}+L_{b}\cdot (h-h_{b})}{T_{b}}}\right]^{\textstyle {\frac {-g_{0}\cdot M}{R^{*}\cdot L_{b}}}}}$

The second equation is used when standard temperature lapse rate equals zero:

${\displaystyle P=P_{b}\cdot \exp \left[{\frac {-g_{0}\cdot M\cdot (h-h_{b})}{R^{*}\cdot T_{b}}}\right]}$

where:

${\displaystyle P_{b}}$ = reference pressure (Pa)

${\displaystyle T_{b}}$ = reference temperature (K)

${\displaystyle L_{b}}$ = temperature lapse rate (K/m) in ISA

${\displaystyle h}$ = height at which pressure is calculated (m)

${\displaystyle h_{b}}$ = height of reference level b (meters; e.g., h_b = 11 000 m)

${\displaystyle R^{*}}$ = universal gas constant: 8.3144598 J/(mol·K)

${\displaystyle g_{0}}$ = gravitational acceleration: 9.80665 m/s²

${\displaystyle M}$ = molar mass of Earth's air: 0.0289644 kg/mol

Or converted to imperial units:^[1]

where

${\displaystyle P_{b}}$ = reference pressure (inches of mercury, inHg)

${\displaystyle T_{b}}$ = reference temperature (K)

${\displaystyle L_{b}}$ = temperature lapse rate (K/ft) in ISA

${\displaystyle h}$ = height at which pressure is calculated (ft)

${\displaystyle h_{b}}$ = height of reference level b (feet; e.g., h_b = 36,089 ft)

${\displaystyle R^{*}}$ = universal gas constant; using feet, kelvins, and (SI) moles: 8.9494596×10⁴ lb·ft²/(lb-mol·K·s²)

${\displaystyle g_{0}}$ = gravitational acceleration: 32.17405 ft/s²

${\displaystyle M}$ = molar mass of Earth's air: 28.9644 lb/lb-mol

The value of subscript b ranges from 0 to 6 in accordance with each of seven successive layers of the atmosphere shown in the table below. In these equations, g₀, M and R^* are each single-valued constants, while P, L, T, and h are multivalued constants in accordance with the table below. The values used for M, g₀, and R^* are in accordance with the U.S. Standard Atmosphere, 1976, and the value for R^* in particular does not agree with standard values for this constant.^[2] The reference value for P_b for b = 0 is the defined sea level value, P₀ = 101 325 Pa or 29.92126 inHg. Values of P_b of b = 1 through b = 6 are obtained from the application of the appropriate member of the pair equations 1 and 2 for the case when h = h_b+1.^[2]

Density equations[]

The expressions for calculating density are nearly identical to calculating pressure. The only difference is the exponent in Equation 1.

There are two different equations for computing density at various height regimes below 86 geometric km (84 852 geopotential meters or 278 385.8 geopotential feet). The first equation is used when the value of standard temperature lapse rate is not equal to zero; the second equation is used when standard temperature lapse rate equals zero.

Equation 1:

${\displaystyle {\rho }=\rho _{b}\cdot \left[{\frac {T_{b}}{T_{b}+L_{b}\cdot (h-h_{b})}}\right]^{\left(1+{\frac {g_{0}\cdot M}{R^{*}\cdot L_{b}}}\right)}}$

Equation 2:

${\displaystyle {\rho }=\rho _{b}\cdot \exp \left[{\frac {-g_{0}\cdot M\cdot (h-h_{b})}{R^{*}\cdot T_{b}}}\right]}$

where

${\displaystyle {\rho }}$ = mass density (kg/m³)

${\displaystyle T_{b}}$ = standard temperature (K)

${\displaystyle L}$ = standard temperature lapse rate (see table below) (K/m) in ISA

${\displaystyle h}$ = height above sea level (geopotential meters)

${\displaystyle R^{*}}$ = universal gas constant 8.3144598 N·m/(mol·K)

${\displaystyle g_{0}}$ = gravitational acceleration: 9.80665 m/s²

${\displaystyle M}$ = molar mass of Earth's air: 0.0289644 kg/mol

or, converted to English gravitational foot-pound-second units:^[1]

${\displaystyle {\rho }}$ = mass density (slug/ft³)

${\displaystyle {T_{b}}}$ = standard temperature (K)

${\displaystyle {L}}$ = standard temperature lapse rate (K/ft)

${\displaystyle {h}}$ = height above sea level (geopotential feet)

${\displaystyle {R^{*}}}$ = universal gas constant: 8.9494596×10⁴ ft²/(s·K)

${\displaystyle {g_{0}}}$ = gravitational acceleration: 32.17405 ft/s²

${\displaystyle {M}}$ = molar mass of Earth's air: 0.0289644 kg/mol

The value of subscript b ranges from 0 to 6 in accordance with each of seven successive layers of the atmosphere shown in the table below. The reference value for ρ_b for b = 0 is the defined sea level value, ρ₀ = 1.2250 kg/m³ or 0.0023768908 slug/ft³. Values of ρ_b of b = 1 through b = 6 are obtained from the application of the appropriate member of the pair equations 1 and 2 for the case when h = h_b+1.^[2]

In these equations, g₀, M and R^* are each single-valued constants, while ρ, L, T and h are multi-valued constants in accordance with the table below. The values used for M, g₀ and R^* are in accordance with the U.S. Standard Atmosphere, 1976, and that the value for R^* in particular does not agree with standard values for this constant.^[2]

Subscript b	Height Above Sea Level (h)		Mass Density (${\displaystyle \rho }$)		Standard Temperature (T') (K)	Temperature Lapse Rate (L)
	(m)	(ft)	(kg/m3)	(slug/ft3)		(K/m)	(K/ft)
0	0	0	1.2250	2.3768908 x 10−3	288.15	-0.0065	-0.0019812
1	11 000	36,089.24	0.36391	7.0611703 x 10−4	216.65	0.0	0.0
2	20 000	65,616.79	0.08803	1.7081572 x 10−4	216.65	0.001	0.0003048
3	32 000	104,986.87	0.01322	2.5660735 x 10−5	228.65	0.0028	0.00085344
4	47 000	154,199.48	0.00143	2.7698702 x 10−6	270.65	0.0	0.0
5	51 000	167,322.83	0.00086	1.6717895 x 10−6	270.65	-0.0028	-0.00085344
6	71 000	232,939.63	0.000064	1.2458989 x 10−7	214.65	-0.002	-0.0006096

Derivation[]

The barometric formula can be derived using the ideal gas law:

${\displaystyle P={\frac {\rho }{M}}\cdot {R^{*}}T}$

Assuming that all pressure is hydrostatic:

${\displaystyle dP=-\rho g\,dz\,}$

and dividing the ${\displaystyle dP}$ by the ${\displaystyle P}$ expression we get:

${\displaystyle {\frac {dP}{P}}=-{\frac {Mg\,dz}{R^{*}T}}}$

Integrating this expression from the surface to the altitude z we get:

${\displaystyle P=P_{0}e^{-\int _{0}^{z}{Mgdz/R^{*}T}}\,}$

Assuming linear temperature change ${\displaystyle T=T_{0}+L\cdot z}$ and constant molar mass and gravitational acceleration, we get the first barometric formula:

${\displaystyle P=P_{0}\cdot \left[{\frac {T_{0}}{T}}\right]^{\textstyle {\frac {Mg}{R^{*}L}}}}$

Instead, assuming constant temperature, integrating gives the second barometric formula:

${\displaystyle P=P_{0}e^{-Mgz/R^{*}T}\,}$

In this formulation, R^* is the gas constant, and the term R^*T/Mg gives the scale height (approximately equal to 8.4 km for the troposphere).

(For exact results, it should be remembered that atmospheres containing water do not behave as an ideal gas. See real gas or perfect gas or gas for further understanding.)

See also[]

• Hypsometric equation
• NRLMSISE-00
• Vertical pressure variation

References[]