Sequence of numbers ((2n) choose (n))
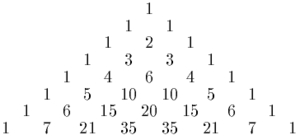
Pascal's triangle, rows 0 through 7. The numbers in the central column are the central binomial coefficients.
In mathematics the n th central binomial coefficient is the particular binomial coefficient
(
2
n
n
)
=
(
2
n
)
!
(
n
!
)
2
=
∏
k
=
1
n
n
+
k
k
for all
n
≥
0.
{\displaystyle {2n \choose n}={\frac {(2n)!}{(n!)^{2}}}=\prod \limits _{k=1}^{n}{\frac {n+k}{k}}{\text{ for all }}n\geq 0.}
They are called central since they show up exactly in the middle of the even-numbered rows in Pascal's triangle . The first few central binomial coefficients starting at n = 0 are:
1 , 2 , 6 , 20 , 70 , 252 , 924, 3432, 12870, 48620, ...; (sequence A000984 OEIS )Properties [ ] The central binomial coefficients represent the number of combinations of a set where there are an equal number of two types of objects.
For example,
n
=
2
{\displaystyle n=2}
AABB, ABAB, ABBA, BAAB, BABA, BBAA .
They also represent the number of combinations of A and B where there are never more B 's than A 's.
For example,
n
=
2
{\displaystyle n=2}
AAAA, AAAB, AABA, AABB, ABAA, ABAB .
The number of factors of 2 in
(
2
n
n
)
{\displaystyle {\binom {2n}{n}}}
binary representation of n ,[1] 1 is the only odd central binomial coefficient.
Generating function [ ] The ordinary generating function for the central binomial coefficients is
1
1
−
4
x
=
∑
n
=
0
∞
(
2
n
n
)
x
n
=
1
+
2
x
+
6
x
2
+
20
x
3
+
70
x
4
+
252
x
5
+
⋯
.
{\displaystyle {\frac {1}{\sqrt {1-4x}}}=\sum _{n=0}^{\infty }{\binom {2n}{n}}x^{n}=1+2x+6x^{2}+20x^{3}+70x^{4}+252x^{5}+\cdots .}
This can be proved using the
binomial series and the relation
(
2
n
n
)
=
(
−
1
)
n
4
n
(
−
1
/
2
n
)
,
{\displaystyle {\binom {2n}{n}}=(-1)^{n}4^{n}{\binom {-1/2}{n}},}
where
(
−
1
/
2
n
)
{\displaystyle \textstyle {\binom {-1/2}{n}}}
is a
generalized binomial coefficient .
[2]
The central binomial coefficients have exponential generating function
∑
n
=
0
∞
(
2
n
n
)
x
n
n
!
=
e
2
x
I
0
(
2
x
)
,
{\displaystyle \sum _{n=0}^{\infty }{\binom {2n}{n}}{\frac {x^{n}}{n!}}=e^{2x}I_{0}(2x),}
where
I 0 is a
modified Bessel function of the first kind .
[3]
The generating function of the squares of the central binomial coefficients can be written in terms of the complete elliptic integral of the first kind :[citation needed
∑
n
=
0
∞
(
2
n
n
)
2
x
n
=
4
π
(
1
+
1
−
16
x
)
K
(
1
−
1
−
16
x
1
+
1
−
16
x
)
.
{\displaystyle \sum _{n=0}^{\infty }{\binom {2n}{n}}^{2}x^{n}={\frac {4}{\pi (1+{\sqrt {1-16x}})}}K\left({\frac {1-{\sqrt {1-16x}}}{1+{\sqrt {1-16x}}}}\right).}
Asymptotic growth [ ] The Wallis product can be written using limits:
π
2
=
lim
n
→
∞
∏
k
=
1
n
2
k
⋅
2
k
(
2
k
−
1
)
(
2
k
+
1
)
=
lim
n
→
∞
4
n
n
!
2
(
2
n
−
1
)
!
!
(
2
n
+
1
)
!
!
=
lim
n
→
∞
4
n
n
!
2
2
2
n
n
!
2
(
2
n
)
!
2
(
2
n
+
1
)
{\displaystyle {\frac {\pi }{2}}=\lim _{n\to \infty }\prod _{k=1}^{n}{\frac {2k\cdot 2k}{(2k-1)(2k+1)}}=\lim _{n\to \infty }{\frac {4^{n}n!^{2}}{(2n-1)!!(2n+1)!!}}=\lim _{n\to \infty }4^{n}n!^{2}{\frac {2^{2n}n!^{2}}{(2n)!^{2}(2n+1)}}}
because
(
2
n
)
!
=
2
n
n
!
(
2
n
−
1
)
!
!
{\displaystyle (2n)!=2^{n}n!(2n-1)!!}
Taking the square root of both sides gives the asymptote for the central binomial coefficient:
(
2
n
n
)
∼
4
n
π
n
{\displaystyle {2n \choose n}\sim {\frac {4^{n}}{\sqrt {\pi n}}}}
The latter can also be established by means of Stirling's formula . On the other hand, it can also be used as a means to determine the constant
2
π
{\displaystyle {\sqrt {2\pi }}}
Approximations [ ] Simple bounds that immediately follow from
4
n
=
(
1
+
1
)
2
n
=
∑
k
=
0
2
n
(
2
n
k
)
{\displaystyle 4^{n}=(1+1)^{2n}=\sum _{k=0}^{2n}{\binom {2n}{k}}}
4
n
2
n
+
1
≤
(
2
n
n
)
≤
4
n
for all
n
≥
0
{\displaystyle {\frac {4^{n}}{2n+1}}\leq {2n \choose n}\leq 4^{n}{\text{ for all }}n\geq 0}
Some better bounds are
4
n
π
(
n
+
1
2
)
≤
(
2
n
n
)
≤
4
n
π
n
for all
n
≥
1
{\displaystyle {\frac {4^{n}}{\sqrt {\pi (n+{\frac {1}{2}})}}}\leq {2n \choose n}\leq {\frac {4^{n}}{\sqrt {\pi n}}}{\text{ for all }}n\geq 1}
Related sequences [ ] The closely related Catalan numbers C n
C
n
=
1
n
+
1
(
2
n
n
)
=
(
2
n
n
)
−
(
2
n
n
+
1
)
for all
n
≥
0.
{\displaystyle C_{n}={\frac {1}{n+1}}{2n \choose n}={2n \choose n}-{2n \choose n+1}{\text{ for all }}n\geq 0.}
A slight generalization of central binomial coefficients is to take them as
Γ
(
2
n
+
1
)
Γ
(
n
+
1
)
2
=
1
n
B
(
n
+
1
,
n
)
{\displaystyle {\frac {\Gamma (2n+1)}{\Gamma (n+1)^{2}}}={\frac {1}{n\mathrm {B} (n+1,n)}}}
n , where
Γ
(
x
)
{\displaystyle \Gamma (x)}
gamma function and
B
(
x
,
y
)
{\displaystyle \mathrm {B} (x,y)}
beta function .
The powers of two that divide the central binomial coefficients are given by Gould's sequence , whose n th element is the number of odd integers in row n of Pascal's triangle.
Squaring the generating function gives
1
1
−
4
x
=
∑
n
=
0
∞
(
2
n
n
)
x
n
∑
n
=
0
∞
(
2
n
n
)
x
n
{\displaystyle {\frac {1}{1-4x}}=\sum _{n=0}^{\infty }{\binom {2n}{n}}x^{n}\sum _{n=0}^{\infty }{\binom {2n}{n}}x^{n}}
Comparing the coefficients of
x
n
{\displaystyle x^{n}}
∑
k
=
0
n
(
2
k
k
)
(
2
n
−
2
k
n
−
k
)
=
4
n
{\displaystyle \sum _{k=0}^{n}{\binom {2k}{k}}{\binom {2n-2k}{n-k}}=4^{n}}
For example,
64
=
1
(
20
)
+
2
(
6
)
+
6
(
2
)
+
20
(
1
)
{\displaystyle 64=1(20)+2(6)+6(2)+20(1)}
A000302 OEIS )
Other information [ ] Half the central binomial coefficient
1
2
(
2
n
n
)
=
(
2
n
−
1
n
−
1
)
{\displaystyle \textstyle {\frac {1}{2}}{2n \choose n}={2n-1 \choose n-1}}
n
>
0
{\displaystyle n>0}
A001700 OEIS ) is seen in Wolstenholme's theorem .
By the Erdős squarefree conjecture , proved in 1996, no central binomial coefficient with n > 4 is squarefree .
(
2
n
n
)
{\displaystyle \textstyle {\binom {2n}{n}}}
n -th row of Pascal's Triangle:[3]
(
2
n
n
)
=
∑
k
=
0
n
(
n
k
)
2
{\displaystyle {2n \choose n}=\sum _{k=0}^{n}{\binom {n}{k}}^{2}}
For example,
(
6
3
)
=
20
=
1
2
+
3
2
+
3
2
+
1
2
{\displaystyle {\tbinom {6}{3}}=20=1^{2}+3^{2}+3^{2}+1^{2}}
Erdős uses central binomial coefficients extensively in his proof of Bertrand's postulate .
Another noteworthy fact is that the power of 2 dividing
(
n
+
1
)
…
(
2
n
)
{\displaystyle (n+1)\dots (2n)}
n .
References [ ] Koshy, Thomas (2008), Catalan Numbers with Applications , Oxford University Press, ISBN 978-0-19533-454-8 External links [ ]