Glossary of module theory

Module theory is the branch of mathematics in which modules are studied. This is a glossary of some terms of the subject.

See also: Glossary of ring theory, Glossary of representation theory.

A[]

algebraically compact

algebraically compact module (also called pure injective module) is a module in which all systems of equations can be decided by finitary means. Alternatively, those modules which leave pure-exact sequence exact after applying Hom.

annihilator

1.  The annihilator of a left ${\displaystyle R}$-module ${\displaystyle M}$ is the set ${\displaystyle {\textrm {Ann}}(M):=\{r\in R|rm=0\,\forall m\in M\}}$ . It is a (left) ideal of ${\displaystyle R}$.

2.  The annihilator of an element ${\displaystyle m\in M}$ is the set ${\displaystyle {\textrm {Ann}}(m):=\{r\in R|rm=0\}}$.

Artinian

An Artinian module is a module in which every decreasing chain of submodules becomes stationary after finitely many steps.

associated prime

1.  An associated prime.

Azumaya

Azumaya's theorem says that two decompositions into modules with local endomorphism rings are equivalent.

B[]

balanced

balanced module

basis

A basis of a module ${\displaystyle M}$ is a set of elements in ${\displaystyle M}$ such that every element in the module can be expressed as a finite sum of elements in the basis in a unique way.

Beauville–Laszlo

Beauville–Laszlo theorem

bimdule

bimodule

C[]

character

character module

coherent

A coherent module is a finitely generated module whose finitely generated submodules are finitely presented.

completely reducible

Synonymous to "semisimple module".

composition

Jordan Hölder composition series

continuous

continuous module

cyclic

A module is called a cyclic module if it is generated by one element.

D[]

D

A D-module is a module over a ring of differential operators.

dense

dense submodule

direct sum

A direct sum of modules is a module that is the direct sum of the underlying abelian group together with component-wise scalar multiplication.

dual module

The dual module of a module M over a commutative ring R is the module ${\displaystyle \operatorname {Hom} _{R}(M,R)}$.

Drinfeld

A Drinfeld module is a module over a ring of functions on algebraic curve with coefficients from a finite field.

E[]

Eilenberg–Mazur

Eilenberg–Mazur swindle

elementary

elementary divisor

endomorphism

The endomorphism ring.

essential

Given a module M, an essential submodule N of M is a submodule that every nonzero submodule of M intersects non-trivially.

Ext functor

Ext functor.

extension

Extension of scalars uses a ring homomorphism from R to S to convert R-modules to S-modules.

F[]

faithful

A faithful module ${\displaystyle M}$ is one where the action of each nonzero ${\displaystyle r\in R}$ on ${\displaystyle M}$ is nontrivial (i.e. ${\displaystyle rx\neq 0}$ for some ${\displaystyle x}$ in ${\displaystyle M}$). Equivalently, ${\displaystyle {\textrm {Ann}}(M)}$ is the zero ideal.

finite

The term "finite module" is another name for a finitely generated module.

finite length

A module of finite length is a module that admits a (finite) composition series.

finite presentation

1.  A finite free presentation of a module M is an exact sequence ${\displaystyle F_{1}\to F_{0}\to M}$ where ${\displaystyle F_{i}}$ are finitely generated free modules.

2.  A finitely presented module is a module that admits a finite free presentation.

finitely generated

A module ${\displaystyle M}$ is finitely generated if there exist finitely many elements ${\displaystyle x_{1},...,x_{n}}$ in ${\displaystyle M}$ such that every element of ${\displaystyle M}$ is a finite linear combination of those elements with coefficients from the scalar ring ${\displaystyle R}$.

fitting

fitting ideal

five

Five lemma.

flat

A ${\displaystyle R}$-module ${\displaystyle F}$ is called a flat module if the tensor product functor ${\displaystyle -\otimes _{R}F}$ is exact.
In particular, every projective module is flat.

free

A free module is a module that has a basis, or equivalently, one that is isomorphic to a direct sum of copies of the scalar ring ${\displaystyle R}$.

G[]

Galois

A Galois module is a module over the group ring of a Galois group.

H[]

graded

A module ${\displaystyle M}$ over a graded ring ${\displaystyle A=\bigoplus _{n\in \mathbb {N} }A_{n}}$ is a graded module if ${\displaystyle M}$ can be expressed as a direct sum ${\displaystyle \bigoplus _{i\in \mathbb {N} }M_{i}}$ and ${\displaystyle A_{i}M_{j}\subseteq M_{i+j}}$.

homomorphism

For two left ${\displaystyle R}$-modules ${\displaystyle M_{1},M_{2}}$, a group homomorphism ${\displaystyle \phi :M_{1}\to M_{2}}$ is called homomorphism of ${\displaystyle R}$-modules if ${\displaystyle r\phi (m)=\phi (rm)\,\forall r\in R,m\in M_{1}}$ .

Hom

Hom functor.

I[]

indecomposable

An indecomposable module is a non-zero module that cannot be written as a direct sum of two non-zero submodules. Every simple module is indecomposable (but not conversely).

injective

1.  A ${\displaystyle R}$-module ${\displaystyle Q}$ is called an injective module if given a ${\displaystyle R}$-module homomorphism ${\displaystyle g:X\to Q}$, and an injective ${\displaystyle R}$-module homomorphism ${\displaystyle f:X\to Y}$, there exists a ${\displaystyle R}$-module homomorphism ${\displaystyle h:Y\to Q}$ such that ${\displaystyle f\circ h=g}$ .

The module Q is injective if the diagram commutes

The following conditions are equivalent:

• The contravariant functor ${\displaystyle {\textrm {Hom}}_{R}(-,I)}$ is exact.
• ${\displaystyle I}$ is a injective module.
• Every short exact sequence ${\displaystyle 0\to I\to L\to L'\to 0}$ is split.

2.  An injective envelope is a maximal essential extension, or a minimal embedding in an injective module.

3.  An injective cogenerator is an injective module such that every module has a nonzero homomorphism into it.

invariant

invariants

invertible

An invertible module over a commutative ring is a rank-one finite projective module.

irreducible module

Another name for a simple module.

J[]

Jacobson

density theorem

K[]

Kaplansky

Kaplansky's theorem on a projective module says that a projective module over a local ring is free.

Krull–Schmidt

The Krull–Schmidt theorem says that (1) a finite-length module admits an indecomposable decomposition and (2) any two indecomposable decompositions of it are equivalent.

L[]

length

The length of a module is the common length of any composition series of the module; the length is infinite if there is no composition series. Over a field, the length is more commonly known as the dimension.

localization

Localization of a module converts R modules to S modules, where S is a localization of R.

M[]

Mitchell's embedding theorem

Mitchell's embedding theorem

Mittag-Leffler

Mittag-Leffler condition (ML)

module

1.  A left module ${\displaystyle M}$ over the ring ${\displaystyle R}$ is an abelian group ${\displaystyle (M,+)}$ with an operation ${\displaystyle R\times M\to M}$ (called scalar multipliction) satisfies the following condition:

${\displaystyle \forall r,s\in R,m,n\in M}$,

1. ${\displaystyle r(m+n)=rm+rn}$
2. ${\displaystyle r(sm)=(rs)m}$
3. ${\displaystyle 1_{R}\,m=m}$

2.  A right module ${\displaystyle M}$ over the ring ${\displaystyle R}$ is an abelian group ${\displaystyle (M,+)}$ with an operation ${\displaystyle M\times R\to M}$ satisfies the following condition:

${\displaystyle \forall r,s\in R,m,n\in M}$,

1. ${\displaystyle (m+n)r=mr+nr}$
2. ${\displaystyle (ms)r=r(sm)}$
3. ${\displaystyle m1_{R}=m}$

3.  All the modules together with all the module homomorphisms between them form the category of modules.

N[]

Noetherian

A Noetherian module is a module such that every submodule is finitely generated. Equivalently, every increasing chain of submodules becomes stationary after finitely many steps.

normal

normal forms for matrices

P[]

principal

A principal indecomposable module is a cyclic indecomposable projective module.

primary

A primary submodule

projective

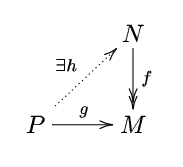The characteristic property of projective modules is called lifting.

A ${\displaystyle R}$-module ${\displaystyle P}$ is called a projective module if given a ${\displaystyle R}$-module homomorphism ${\displaystyle g:P\to M}$, and a surjective ${\displaystyle R}$-module homomorphism ${\displaystyle f:N\to M}$, there exists a ${\displaystyle R}$-module homomorphism ${\displaystyle h:P\to N}$ such that ${\displaystyle f\circ h=g}$ .

The following conditions are equivalent:

• The covariant functor ${\displaystyle {\textrm {Hom}}_{R}(P,-)}$ is exact.
• ${\displaystyle M}$ is a projective module.
• Every short exact sequence ${\displaystyle 0\to L\to L'\to P\to 0}$ is split.
• ${\displaystyle M}$ is a direct summand of free modules.

In particular, every free module is projective.

2.  The projective dimension of a module is the minimal length of (if any) a finite projective resolution of the module; the dimension is infinite if there is no finite projective resolution.

3.  A projective cover is a minimal surjection from a projective module.

Q[]

quotient

Given a left ${\displaystyle R}$-module ${\displaystyle M}$ and a submodule ${\displaystyle N}$, the quotient group ${\displaystyle M/N}$ can be made to be a left ${\displaystyle R}$-module by ${\displaystyle r(m+N)=rm+N}$ for ${\displaystyle r\in R,\,m\in M}$. It is called a quotient module or factor module.

R[]

radical

The radical of a module is the intersection of the maximal submodules. For Artinian modules, the smallest submodule with semisimple quotient.

rational

rational canonical form

reflexive

A reflexive module is a module that is isomorphic via the natural map to its second dual.

resolution

resolution

restriction

Restriction of scalars uses a ring homomorphism from R to S to convert S-modules to R-modules.

S[]

Schanuel

Schanuel's lemma

snake

Snake lemma

socle

The socle is the largest semisimple submodule.

semisimple

A semisimple module is a direct sum of simple modules.

simple

A simple module is a nonzero module whose only submodules are zero and itself.

stably free

A stably free module

structure theorem

The structure theorem for finitely generated modules over a principal ideal domain says that a finitely generated modules over PIDs are finite direct sums of primary cyclic modules.

submodule

Given a ${\displaystyle R}$-module ${\displaystyle M}$, an additive subgroup ${\displaystyle N}$ of ${\displaystyle M}$ is a submodule if ${\displaystyle RN\subset N}$.

support

The support of a module over a commutative ring is the set of prime ideals at which the localizations of the module are nonzero.

T[]

tensor

Tensor product of modules

Tor

Tor functor.

torsionless

A torsionless module.

U[]

uniform

A uniform module is a module in which every two non-zero submodules have a non-zero intersection.

References[]

• John A. Beachy (1999). Introductory Lectures on Rings and Modules (1st ed.). Addison-Wesley. ISBN 0-521-64407-0.
• Golan, Jonathan S.; Head, Tom (1991), Modules and the structure of rings, Monographs and Textbooks in Pure and Applied Mathematics, vol. 147, Marcel Dekker, ISBN 978-0-8247-8555-0, MR 1201818
• Lam, Tsit-Yuen (1999), Lectures on modules and rings, Graduate Texts in Mathematics No. 189, Berlin, New York: Springer-Verlag, ISBN 978-0-387-98428-5, MR 1653294
• Serge Lang (1993). Algebra (3rd ed.). Addison-Wesley. ISBN 0-201-55540-9.
• Passman, Donald S. (1991), A course in ring theory, The Wadsworth & Brooks/Cole Mathematics Series, Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced Books & Software, ISBN 978-0-534-13776-2, MR 1096302