Gravitational potential

Plot of a two-dimensional slice of the gravitational potential in and around a uniform spherical body. The inflection points of the cross-section are at the surface of the body.

In classical mechanics, the gravitational potential at a location is equal to the work (energy transferred) per unit mass that would be needed to move an object to that location from a fixed reference location. It is analogous to the electric potential with mass playing the role of charge. The reference location, where the potential is zero, is by convention infinitely far away from any mass, resulting in a negative potential at any finite distance.

In mathematics, the gravitational potential is also known as the Newtonian potential and is fundamental in the study of potential theory. It may also be used for solving the electrostatic and magnetostatic fields generated by uniformly charged or polarized ellipsoidal bodies.^[1]

Potential energy[]

The gravitational potential (V) at a location is the gravitational potential energy (U) at that location per unit mass:

${\displaystyle V={\frac {U}{m}},}$

where m is the mass of the object. Potential energy is equal (in magnitude, but negative) to the work done by the gravitational field moving a body to its given position in space from infinity. If the body has a mass of 1 kilogram, then the potential energy to be assigned to that body is equal to the gravitational potential. So the potential can be interpreted as the negative of the work done by the gravitational field moving a unit mass in from infinity.

In some situations, the equations can be simplified by assuming a field that is nearly independent of position. For instance, in a region close to the surface of the Earth, the gravitational acceleration, g, can be considered constant. In that case, the difference in potential energy from one height to another is, to a good approximation, linearly related to the difference in height:

${\displaystyle \Delta U\approx mg\Delta h.}$

Mathematical form[]

The gravitational potential V at a distance x from a point mass of mass M can be defined as the work W that needs to be done by an external agent to bring a unit mass in from infinity to that point:^[2][3][4][5]

${\displaystyle V(\mathbf {x} )={\frac {W}{m}}={\frac {1}{m}}\int \limits _{\infty }^{x}\mathbf {F} \cdot d\mathbf {x} ={\frac {1}{m}}\int \limits _{\infty }^{x}{\frac {GmM}{x^{2}}}dx=-{\frac {GM}{x}},}$

where G is the gravitational constant, and F is the gravitational force. The product GM is the standard gravitational parameter and is often known to higher precision than G or M separately. The potential has units of energy per mass, e.g., J/kg in the MKS system. By convention, it is always negative where it is defined, and as x tends to infinity, it approaches zero.

The gravitational field, and thus the acceleration of a small body in the space around the massive object, is the negative gradient of the gravitational potential. Thus the negative of a negative gradient yields positive acceleration toward a massive object. Because the potential has no angular components, its gradient is

${\displaystyle \mathbf {a} =-{\frac {GM}{x^{3}}}\mathbf {x} =-{\frac {GM}{x^{2}}}{\hat {\mathbf {x} }},}$

where x is a vector of length x pointing from the point mass toward the small body and ${\displaystyle {\hat {\mathbf {x} }}}$ is a unit vector pointing from the point mass toward the small body. The magnitude of the acceleration therefore follows an inverse square law:

${\displaystyle |\mathbf {a} |={\frac {GM}{x^{2}}}.}$

The potential associated with a mass distribution is the superposition of the potentials of point masses. If the mass distribution is a finite collection of point masses, and if the point masses are located at the points x₁, ..., x_n and have masses m₁, ..., m_n, then the potential of the distribution at the point x is

${\displaystyle V(\mathbf {x} )=\sum _{i=1}^{n}-{\frac {Gm_{i}}{|\mathbf {x} -\mathbf {x_{i}} |}}.}$

Points x and r, with r contained in the distributed mass (gray) and differential mass dm(r) located at the point r.

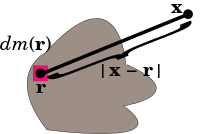
If the mass distribution is given as a mass measure dm on three-dimensional Euclidean space R³, then the potential is the convolution of −G/|r| with dm.^[6] In good cases^{[clarification needed]} this equals the integral

${\displaystyle V(\mathbf {x} )=-\int _{\mathbf {R} ^{3}}{\frac {G}{|\mathbf {x} -\mathbf {r} |}}\,dm(\mathbf {r} ),}$

where |x − r| is the distance between the points x and r. If there is a function ρ(r) representing the density of the distribution at r, so that dm(r)= ρ(r)dv(r), where dv(r) is the Euclidean volume element, then the gravitational potential is the volume integral

${\displaystyle V(\mathbf {x} )=-\int _{\mathbf {R} ^{3}}{\frac {G}{|\mathbf {x} -\mathbf {r} |}}\,\rho (\mathbf {r} )dv(\mathbf {r} ).}$

If V is a potential function coming from a continuous mass distribution ρ(r), then ρ can be recovered using the Laplace operator, Δ:

${\displaystyle \rho (\mathbf {x} )={\frac {1}{4\pi G}}\Delta V(\mathbf {x} ).}$

This holds pointwise whenever ρ is continuous and is zero outside of a bounded set. In general, the mass measure dm can be recovered in the same way if the Laplace operator is taken in the sense of distributions. As a consequence, the gravitational potential satisfies Poisson's equation. See also Green's function for the three-variable Laplace equation and Newtonian potential.

The integral may be expressed in terms of known transcendental functions for all ellipsoidal shapes, including the symmetrical and degenerate ones.^[7] These include the sphere, where the three semiaxes are equal; the oblate (see reference ellipsoid) and prolate spheroids, where two semiaxes are equal; the degenerate ones where one semiaxis is infinite (the elliptical and circular cylinder) and the unbounded sheet where two semiaxes are infinite. All these shapes are widely used in the applications of the gravitational potential integral (apart from the constant G, with