Initial topology

In general topology and related areas of mathematics, the initial topology (or induced topology^[1][2] or weak topology or limit topology or projective topology) on a set ${\displaystyle X}$, with respect to a family of functions on ${\displaystyle X}$, is the coarsest topology on X that makes those functions continuous.

The subspace topology and product topology constructions are both special cases of initial topologies. Indeed, the initial topology construction can be viewed as a generalization of these.

The dual notion is the final topology, which for a given family of functions mapping to a set ${\displaystyle X}$ is the finest topology on ${\displaystyle X}$ that makes those functions continuous.

Definition[]

Given a set X and an indexed family (Y_i)_i∈I of topological spaces with functions

${\displaystyle f_{i}:X\to Y_{i},}$

the initial topology ${\displaystyle \tau }$ on ${\displaystyle X}$ is the coarsest topology on X such that each

${\displaystyle f_{i}:(X,\tau )\to Y_{i}}$

is continuous.

Explicitly, the initial topology is the collection of open sets generated by all sets of the form ${\displaystyle f_{i}^{-1}(U)}$, where ${\displaystyle U}$ is an open set in ${\displaystyle Y_{i}}$ for some i ∈ I, under finite intersections and arbitrary unions. The sets ${\displaystyle f_{i}^{-1}(U)}$ are often called cylinder sets. If I contains exactly one element, all the open sets of ${\displaystyle (X,\tau )}$ are cylinder sets.

Examples[]

Several topological constructions can be regarded as special cases of the initial topology.

• The subspace topology is the initial topology on the subspace with respect to the inclusion map.
• The product topology is the initial topology with respect to the family of projection maps.
• The inverse limit of any inverse system of spaces and continuous maps is the set-theoretic inverse limit together with the initial topology determined by the canonical morphisms.
• The weak topology on a locally convex space is the initial topology with respect to the continuous linear forms of its dual space.
• Given a family of topologies {τ_i} on a fixed set X the initial topology on X with respect to the functions id_i : X → (X, τ_i) is the supremum (or join) of the topologies {τ_i} in the lattice of topologies on X. That is, the initial topology τ is the topology generated by the union of the topologies {τ_i}.
• A topological space is completely regular if and only if it has the initial topology with respect to its family of (bounded) real-valued continuous functions.
• Every topological space X has the initial topology with respect to the family of continuous functions from X to the Sierpiński space.

Properties[]

Characteristic property[]

The initial topology on X can be characterized by the following characteristic property:
A function ${\displaystyle g}$ from some space ${\displaystyle Z}$ to ${\displaystyle X}$ is continuous if and only if ${\displaystyle f_{i}\circ g}$ is continuous for each i ∈ I.

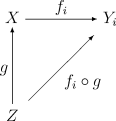
Note that, despite looking quite similar, this is not a universal property. A categorical description is given below.

Evaluation[]

By the universal property of the product topology, we know that any family of continuous maps ${\displaystyle f_{i}\colon X\to Y_{i}}$ determines a unique continuous map

${\displaystyle f\colon X\to \prod _{i}Y_{i}\,.}$

This map is known as the evaluation map.

A family of maps ${\displaystyle \{f_{i}\colon X\to Y_{i}\}}$ is said to separate points in X if for all ${\displaystyle x\neq y}$ in X there exists some i such that ${\displaystyle f_{i}(x)\neq f_{i}(y)}$. Clearly, the family ${\displaystyle \{f_{i}\}}$ separates points if and only if the associated evaluation map f is injective.

The evaluation map f will be a topological embedding if and only if X has the initial topology determined by the maps ${\displaystyle \{f_{i}\}}$ and this family of maps separates points in X.

Separating points from closed sets[]

If a space X comes equipped with a topology, it is often useful to know whether or not the topology on X is the initial topology induced by some family of maps on X. This section gives a sufficient (but not necessary) condition.

A family of maps {f_i: X → Y_i} separates points from closed sets in X if for all closed sets A in X and all x not in A, there exists some i such that

${\displaystyle f_{i}(x)\notin \operatorname {cl} (f_{i}(A))}$

where cl denotes the closure operator.

Theorem. A family of continuous maps {f_i: X → Y_i} separates points from closed sets if and only if the cylinder sets ${\displaystyle f_{i}^{-1}(U)}$, for U open in Y_i, form a base for the topology on X.

It follows that whenever {f_i} separates points from closed sets, the space X has the initial topology induced by the maps {f_i}. The converse fails, since generally the cylinder sets will only form a subbase (and not a base) for the initial topology.

If the space X is a T₀ space, then any collection of maps {f_i} that separates points from closed sets in X must also separate points. In this case, the evaluation map will be an embedding.

Categorical description[]

In the language of category theory, the initial topology construction can be described as follows. Let ${\displaystyle Y}$ be the functor from a discrete category ${\displaystyle J}$ to the category of topological spaces ${\displaystyle \mathrm {Top} }$ which maps ${\displaystyle j\mapsto Y_{j}}$. Let ${\displaystyle U}$ be the usual forgetful functor from ${\displaystyle \mathrm {Top} }$ to ${\displaystyle \mathrm {Set} }$. The maps ${\displaystyle f_{j}:X\to Y_{j}}$ can then be thought of as a cone from ${\displaystyle X}$ to ${\displaystyle UY}$. That is, ${\displaystyle (X,f)}$ is an object of ${\displaystyle \mathrm {Cone} (UY):=(\Delta \downarrow {UY})}$—the category of cones to ${\displaystyle UY}$. More precisely, this cone ${\displaystyle (X,f)}$ defines a ${\displaystyle U}$-structured cosink in ${\displaystyle \mathrm {Set} }$.

The forgetful functor ${\displaystyle U:\mathrm {Top} \to \mathrm {Set} }$ induces a functor ${\displaystyle {\bar {U}}:\mathrm {Cone} (Y)\to \mathrm {Cone} (UY)}$. The characteristic property of the initial topology is equivalent to the statement that there exists a universal morphism from ${\displaystyle {\bar {U}}}$ to ${\displaystyle (X,f)}$, i.e.: a terminal object in the category ${\displaystyle ({\bar {U}}\downarrow (X,f))}$.
Explicitly, this consists of an object ${\displaystyle I(X,f)}$ in ${\displaystyle \mathrm {Cone} (Y)}$ together with a morphism ${\displaystyle \varepsilon :{\bar {U}}I(X,f)\to (X,f)}$ such that for any object ${\displaystyle (Z,g)}$ in ${\displaystyle \mathrm {Cone} (Y)}$ and morphism ${\displaystyle \varphi :{\bar {U}}(Z,g)\to (X,f)}$ there exists a unique morphism ${\displaystyle \zeta :(Z,g)\to I(X,f)}$ such that the following diagram commutes:

The assignment ${\displaystyle (X,f)\mapsto I(X,f)}$ placing the initial topology on ${\displaystyle X}$ extends to a functor ${\displaystyle I:\mathrm {Cone} (UY)\to \mathrm {Cone} (Y)}$ which is right adjoint to the forgetful functor ${\displaystyle {\bar {U}}}$. In fact, ${\displaystyle I}$ is a right-inverse to ${\displaystyle {\bar {U}}}$; since ${\displaystyle {\bar {U}}I}$ is the identity functor on ${\displaystyle \mathrm {Cone} (UY)}$.

See also[]

• Final topology
• Induced topology

References[]

Sources[]

• Willard, Stephen (1970). General Topology. Reading, Massachusetts: Addison-Wesley. ISBN 0-486-43479-6.
• "Initial topology". PlanetMath.
• "Product topology and subspace topology". PlanetMath.