Kampyle of Eudoxus

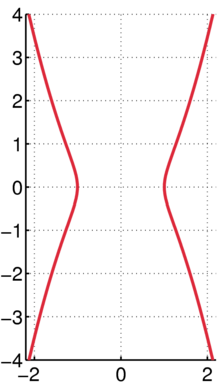
Graph of Kampyle of Eudoxus with a = 1

The Kampyle of Eudoxus (Greek: καμπύλη [γραμμή], meaning simply "curved [line], curve") is a curve with a Cartesian equation of

${\displaystyle x^{4}=a^{2}(x^{2}+y^{2}),}$

from which the solution x = y = 0 is excluded.

Alternative parameterizations[]

In polar coordinates, the Kampyle has the equation

${\displaystyle r=a\sec ^{2}\theta .}$

Equivalently, it has a parametric representation as

${\displaystyle x=a\sec(t),\quad y=a\tan(t)\sec(t).}$

History[]

This quartic curve was studied by the Greek astronomer and mathematician Eudoxus of Cnidus (c. 408 BC – c.347 BC) in relation to the classical problem of doubling the cube.

Properties[]

The Kampyle is symmetric about both the x- and y-axes. It crosses the x-axis at (±a,0). It has inflection points at

${\displaystyle \left(\pm a{\frac {\sqrt {6}}{2}},\pm a{\frac {\sqrt {3}}{2}}\right)}$

(four inflections, one in each quadrant). The top half of the curve is asymptotic to ${\displaystyle x^{2}/a-a/2}$ as ${\displaystyle x\to \infty }$, and in fact can be written as

${\displaystyle y={\frac {x^{2}}{a}}{\sqrt {1-{\frac {a^{2}}{x^{2}}}}}={\frac {x^{2}}{a}}-{\frac {a}{2}}\sum _{n=0}^{\infty }C_{n}\left({\frac {a}{2x}}\right)^{2n},}$

where

${\displaystyle C_{n}={\frac {1}{n+1}}{\binom {2n}{n}}}$

is the ${\displaystyle n}$th Catalan number.

See also[]

• List of curves

References[]

• J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 141–142. ISBN 0-486-60288-5.

External links[]

• O'Connor, John J.; Robertson, Edmund F., "Kampyle of Eudoxus", MacTutor History of Mathematics archive, University of St Andrews
• Weisstein, Eric W. "Kampyle of Eudoxus". MathWorld.