Ladder graph

Ladder graph
The ladder graph L8.
Vertices	2n
Edges	3n-2
Chromatic number	2
Chromatic index	3 for n>2 2 for n=2 1 for n=1
Properties	Unit distance Hamiltonian Planar Bipartite
Notation	Ln
Table of graphs and parameters

In the mathematical field of graph theory, the ladder graph L_n is a planar undirected graph with 2n vertices and 3n-2 edges.^[1]

The ladder graph can be obtained as the Cartesian product of two path graphs, one of which has only one edge: L_n,1 = P_n × P₂.^[2][3]

Properties[]

By construction, the ladder graph L_n is isomorphic to the grid graph G_2,n and looks like a ladder with n rungs. It is Hamiltonian with girth 4 (if n>1) and chromatic index 3 (if n>2).

The chromatic number of the ladder graph is 2 and its chromatic polynomial is ${\displaystyle (x-1)x(x^{2}-3x+3)^{(n-1)}}$.

The ladder graphs L₁, L₂, L₃, L₄ and L₅.

• 

  The chromatic number of the ladder graph is 2.

Ladder rung graph[]

Sometimes the term "ladder graph" is used for the n × P₂ ladder rung graph, which is the graph union of n copies of the path graph P₂.

The ladder rung graphs LR₁, LR₂, LR₃, LR₄, and LR₅.

Circular ladder graph[]

The circular ladder graph CL_n is constructible by connecting the four 2-degree vertices in a straight way, or by the Cartesian product of a cycle of length n≥3 and an edge.^[4] In symbols, CL_n = C_n × P₂. It has 2n nodes and 3n edges. Like the ladder graph, it is connected, planar and Hamiltonian, but it is bipartite if and only if n is even.

Circular ladder graph are the polyhedral graphs of prisms, so they are more commonly called prism graphs.

Circular ladder graphs:

CL3

CL4

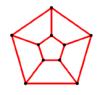CL5

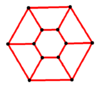CL6

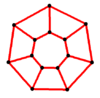CL7

CL8

Möbius ladder[]

Connecting the four 2-degree vertices crosswise creates a cubic graph called a Möbius ladder.

Two views of the Möbius ladder M₁₆ .

References[]