Mathematical functions
The lemniscate sine (red) and lemniscate cosine (purple) applied to a real argument, in comparison with the trigonometric sine
y = sin(πx /ϖ ) (pale dashed red).
In mathematics , the lemniscate elliptic functions are elliptic functions related to the arc length of the lemniscate of Bernoulli . They were first studied by Giulio Fagnano in 1718 and later by Leonhard Euler and Carl Friedrich Gauss , among others.
The lemniscate sine and lemniscate cosine functions, usually written with the symbols sl cl sinlem coslem sin lemn cos lemn [1] trigonometric functions sine and cosine. While the trigonometric sine relates the arc length to the chord length in a unit-diameter circle
x
2
+
y
2
=
x
{\displaystyle x^{2}+y^{2}=x}
(
x
2
+
y
2
)
2
=
x
2
−
y
2
.
{\displaystyle {\bigl (}x^{2}+y^{2}{\bigr )}{}^{2}=x^{2}-y^{2}.}
The lemniscate functions have periods related to a number
ϖ
=
{\displaystyle \varpi =}
lemniscate constant , the ratio of a lemniscate's perimeter to its diameter.
The sl and cl functions have a square period lattice (a multiple of the Gaussian integers ) with fundamental periods
{
(
1
+
i
)
ϖ
,
(
1
−
i
)
ϖ
}
,
{\displaystyle \{(1+i)\varpi ,(1-i)\varpi \},}
[2] Jacobi elliptic functions on that lattice,
sl
z
=
sn
(
z
;
i
)
,
{\displaystyle \operatorname {sl} z=\operatorname {sn} (z;i),}
cl
z
=
cd
(
z
;
i
)
{\displaystyle \operatorname {cl} z=\operatorname {cd} (z;i)}
Similarly, the hyperbolic lemniscate functions slh clh
{
2
ϖ
,
2
ϖ
i
}
.
{\displaystyle {\bigl \{}{\sqrt {2}}\varpi ,{\sqrt {2}}\varpi i{\bigr \}}.}
The lemniscate functions and the hyperbolic lemniscate functions are related to the Weierstrass elliptic function
℘
(
z
;
a
,
0
)
{\displaystyle \wp (z;a,0)}
Lemniscate sine and cosine functions [ ] Definitions [ ] The lemniscate functions sl and cl can be defined as the solution to the initial value problem :[3]
d
d
z
cl
z
=
−
sl
z
(
1
+
cl
2
z
)
,
d
d
z
sl
z
=
cl
z
(
1
+
sl
2
z
)
,
cl
(
0
)
=
1
,
sl
(
0
)
=
0
,
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {cl} z=-\operatorname {sl} z\,{\bigl (}1+\operatorname {cl} ^{2}z{\bigr )},\ {\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {sl} z=\operatorname {cl} z\,{\bigl (}1+\operatorname {sl} ^{2}z{\bigr )},\ \operatorname {cl} (0)=1,\ \operatorname {sl} (0)=0,}
or equivalently as the inverses of an elliptic integral , the Schwarz–Christoffel map from the complex unit disk to a square with corners
{
1
2
ϖ
,
1
2
ϖ
i
,
−
1
2
ϖ
,
−
1
2
ϖ
i
}
:
{\displaystyle {\big \{}{\tfrac {1}{2}}\varpi ,{\tfrac {1}{2}}\varpi i,-{\tfrac {1}{2}}\varpi ,-{\tfrac {1}{2}}\varpi i{\big \}}\colon }
[4]
z
=
∫
0
sl
z
d
t
1
−
t
4
=
∫
cl
z
1
d
t
1
−
t
4
.
{\displaystyle z=\int _{0}^{\operatorname {sl} z}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}=\int _{\operatorname {cl} z}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}.}
Beyond that square, the functions can be analytically continued to the whole complex plane by a series of reflections .
By comparison, the circular sine and cosine can be defined as the solution to the initial value problem:
d
d
z
cos
z
=
−
sin
z
,
d
d
z
sin
z
=
cos
z
,
cos
(
0
)
=
1
,
sin
(
0
)
=
0
,
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\cos z=-\sin z,\ {\frac {\mathrm {d} }{\mathrm {d} z}}\sin z=\cos z,\ \cos(0)=1,\ \sin(0)=0,}
or as inverses of a map from the upper half-plane to a half-infinite strip with real part between
−
1
2
π
,
1
2
π
{\displaystyle -{\tfrac {1}{2}}\pi ,{\tfrac {1}{2}}\pi }
z
=
∫
0
sin
z
d
t
1
−
t
2
=
∫
cos
z
1
d
t
1
−
t
2
.
{\displaystyle z=\int _{0}^{\sin z}{\frac {\mathrm {d} t}{\sqrt {1-t^{2}}}}=\int _{\cos z}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{2}}}}.}
Arc length of Bernoulli's lemniscate [ ]
The lemniscate sine and cosine relate the arc length of an arc of the lemniscate to the distance of one endpoint from the origin.
The trigonometric sine and cosine analogously relate the arc length of an arc of a unit-diameter circle to the distance of one endpoint from the origin.
The lemniscate of Bernoulli with half-width 1 is the locus of points in the plane such that the product of their distances from the two focal points
F
1
=
(
−
1
2
,
0
)
{\displaystyle F_{1}={\bigl (}{-{\tfrac {1}{\sqrt {2}}}},0{\bigr )}}
F
2
=
(
1
2
,
0
)
{\displaystyle F_{2}={\bigl (}{\tfrac {1}{\sqrt {2}}},0{\bigr )}}
1
2
{\displaystyle {\tfrac {1}{2}}}
quartic curve satisfying the polar equation
r
2
=
cos
2
θ
{\displaystyle r^{2}=\cos 2\theta }
Cartesian equation
(
x
2
+
y
2
)
2
=
x
2
−
y
2
.
{\displaystyle {\bigl (}x^{2}+y^{2}{\bigr )}{}^{2}=x^{2}-y^{2}.}
The points on the lemniscate at distance
r
{\displaystyle r}
x
2
+
y
2
=
r
2
{\displaystyle x^{2}+y^{2}=r^{2}}
hyperbola
x
2
−
y
2
=
r
4
{\displaystyle x^{2}-y^{2}=r^{4}}
(
x
(
r
)
,
y
(
r
)
)
=
(
1
2
r
2
(
1
+
r
2
)
,
1
2
r
2
(
1
−
r
2
)
)
.
{\displaystyle {\big (}x(r),y(r){\big )}={\biggl (}\!{\sqrt {{\tfrac {1}{2}}r^{2}{\bigl (}1+r^{2}{\bigr )}}},{\sqrt {{\tfrac {1}{2}}r^{2}{\bigl (}1-r^{2}{\bigr )}}}\,{\biggr )}.}
Using this parametrization with
r
∈
[
0
,
1
]
{\displaystyle r\in [0,1]}
arc length from the origin to a point
(
x
(
r
)
,
y
(
r
)
)
{\displaystyle {\big (}x(r),y(r){\big )}}
[5]
∫
0
r
x
′
(
t
)
2
+
y
′
(
t
)
2
d
t
=
∫
0
r
(
1
+
2
t
2
)
2
2
(
1
+
t
2
)
+
(
1
−
2
t
2
)
2
2
(
1
−
t
2
)
d
t
=
∫
0
r
d
t
1
−
t
4
=
arcsl
r
.
{\displaystyle {\begin{aligned}&\int _{0}^{r}{\sqrt {x'(t)^{2}+y'(t)^{2}}}\mathop {\mathrm {d} t} \\&\quad {}=\int _{0}^{r}{\sqrt {{\frac {(1+2t^{2})^{2}}{2(1+t^{2})}}+{\frac {(1-2t^{2})^{2}}{2(1-t^{2})}}}}\mathop {\mathrm {d} t} \\[6mu]&\quad {}=\int _{0}^{r}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}\\[6mu]&\quad {}=\operatorname {arcsl} r.\end{aligned}}}
Likewise, the arc length from
(
1
,
0
)
{\displaystyle (1,0)}
(
x
(
r
)
,
y
(
r
)
)
{\displaystyle {\big (}x(r),y(r){\big )}}
∫
r
1
x
′
(
t
)
2
+
y
′
(
t
)
2
d
t
=
∫
r
1
d
t
1
−
t
4
=
arccl
r
=
1
2
ϖ
−
arcsl
r
.
{\displaystyle {\begin{aligned}&\int _{r}^{1}{\sqrt {x'(t)^{2}+y'(t)^{2}}}\mathop {\mathrm {d} t} \\&\quad {}=\int _{r}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}\\[6mu]&\quad {}=\operatorname {arccl} r={\tfrac {1}{2}}\varpi -\operatorname {arcsl} r.\end{aligned}}}
Or in the inverse direction, the lemniscate sine and cosine functions give the distance from the origin as functions of arc length from the origin and the point
(
1
,
0
)
{\displaystyle (1,0)}
Analogously, the circular sine and cosine functions relate the chord length to the arc length for the unit diameter circle with polar equation
r
=
cos
θ
{\displaystyle r=\cos \theta }
x
2
+
y
2
=
x
,
{\displaystyle x^{2}+y^{2}=x,}
(
x
(
r
)
,
y
(
r
)
)
=
(
r
2
,
r
2
(
1
−
r
2
)
)
.
{\displaystyle {\big (}x(r),y(r){\big )}={\biggl (}r^{2},{\sqrt {r^{2}{\bigl (}1-r^{2}{\bigr )}}}\,{\biggr )}.}
The lemniscate integral and lemniscate functions satisfy an argument duplication identity discovered by Fagnano in 1718:[6]
∫
0
z
d
t
1
−
t
4
=
2
∫
0
u
d
t
1
−
t
4
,
if
z
=
2
u
1
−
u
4
1
+
u
4
and
0
≤
u
≤
2
−
1
.
{\displaystyle \int _{0}^{z}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}=2\int _{0}^{u}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}},\quad {\text{if }}z={\frac {2u{\sqrt {1-u^{4}}}}{1+u^{4}}}{\text{ and }}0\leq u\leq {\sqrt {{\sqrt {2}}-1}}.}
Later mathematicians generalized this result. Analogously to the constructible polygons in the circle, the lemniscate can be divided into n straightedge and compass whenever n
n
=
2
k
p
1
p
2
⋯
p
m
{\displaystyle n=2^{k}p_{1}p_{2}\cdots p_{m}}
k m integers and each p i Fermat prime .[7] Niels Abel in 1827–1828.[8]
Arc length of rectangular elastica [ ]
The lemniscate sine relates the arc length to the x coordinate in the rectangular elastica.
The inverse lemniscate sine also describes the arc length s x elastica .[9] y
y
=
∫
x
1
t
2
d
t
1
−
t
4
,
s
=
arcsl
x
=
∫
0
x
d
t
1
−
t
4
{\displaystyle y=\int _{x}^{1}{\frac {t^{2}\mathop {\mathrm {d} t} }{\sqrt {1-t^{4}}}},\quad s=\operatorname {arcsl} x=\int _{0}^{x}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}}
The rectangular elastica solves a problem posed by Jacob Bernoulli , in 1691, to describe the shape of an idealized flexible rod fixed in a vertical orientation at the bottom end and pulled down by a weight from the far end until it has been bent horizontal. Bernoulli's proposed solution established Euler–Bernoulli beam theory , further developed by Euler in the 18th century.
Lemniscate constant [ ]
sl
z
{\displaystyle \operatorname {sl} z}
in the complex plane.
[10] In the picture, it can be seen that the fundamental periods
(
1
+
i
)
ϖ
{\displaystyle (1+i)\varpi }
and
(
1
−
i
)
ϖ
{\displaystyle (1-i)\varpi }
are "minimal" in the sense that they have the smallest absolute value of all periods whose real part is non-negative.
The lemniscate functions have minimal real period 2ϖ and fundamental complex periods
(
1
+
i
)
ϖ
{\displaystyle (1+i)\varpi }
(
1
−
i
)
ϖ
{\displaystyle (1-i)\varpi }
ϖ lemniscate constant ,[11]
ϖ
=
2
∫
0
1
d
t
1
−
t
4
=
2
∫
0
∞
d
t
1
+
t
4
=
∫
0
1
d
t
t
−
t
3
=
4
∫
0
∞
(
1
+
t
4
4
−
t
)
d
t
=
2
2
∫
0
1
1
−
t
4
4
d
t
=
3
∫
0
1
1
−
t
4
d
t
=
1
2
B
(
1
4
,
1
2
)
=
Γ
(
1
4
)
2
2
2
π
=
π
M
(
1
,
2
)
=
π
e
β
′
(
0
)
=
2.62205
75542
92119
81046
48395
89891
11941
…
,
{\displaystyle {\begin{aligned}\varpi &=2\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}={\sqrt {2}}\int _{0}^{\infty }{\frac {\mathrm {d} t}{\sqrt {1+t^{4}}}}=\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {t-t^{3}}}}\\[6mu]&=4\int _{0}^{\infty }{\Bigl (}{\sqrt[{4}]{1+t^{4}}}-t{\Bigr )}\,\mathrm {d} t=2{\sqrt {2}}\int _{0}^{1}{\sqrt[{4}]{1-t^{4}}}\mathop {\mathrm {d} t} =3\int _{0}^{1}{\sqrt {1-t^{4}}}\,\mathrm {d} t\\[2mu]&={\tfrac {1}{2}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )}={\frac {\Gamma {\bigl (}{\tfrac {1}{4}}{\bigr )}^{2}}{2{\sqrt {2\pi }}}}={\frac {\pi }{{\operatorname {M} }{\bigl (}1,{\sqrt {2}}{\bigr )}}}={\sqrt {\pi }}e^{\beta '(0)}\\[5mu]&=2.62205\;75542\;92119\;81046\;48395\;89891\;11941\ldots ,\end{aligned}}}
where Β is the beta function , Γ is the gamma function ,
M is the arithmetic–geometric mean and β' is the derivative of the Dirichlet beta function . Geometrically, ϖ perimeter of Bernoulli's lemniscate to its diameter . The lemniscate constant was proven transcendental by Theodor Schneider in 1937.[12] Gregory Chudnovsky proved that π and ϖ algebraically independent over
Q
{\displaystyle \mathbb {Q} }
[13] [14]
G
=
ϖ
/
π
=
0.8346
…
{\displaystyle G=\varpi /\pi =0.8346\ldots }
Gauss's constant .
The lemniscate constant is twice the value of the complete lemniscate integral.
The lemniscate functions satisfy the basic relation
cl
z
=
sl
(
1
2
ϖ
−
z
)
.
{\displaystyle \operatorname {cl} z={\operatorname {sl} }{\bigl (}{\tfrac {1}{2}}\varpi -z{\bigr )}.}
Furthermore, ϖ
x
4
+
y
4
=
1
{\displaystyle x^{4}+y^{4}=1}
π
n
:=
B
(
1
n
,
1
n
)
{\displaystyle \pi _{n}\mathrel {:=} \mathrm {B} {\bigl (}{\tfrac {1}{n}},{\tfrac {1}{n}}{\bigr )}}
x
n
+
y
n
=
1
{\displaystyle x^{n}+y^{n}=1}
2
∫
0
1
1
−
x
n
n
d
x
=
1
n
π
n
.
{\textstyle 2\int _{0}^{1}{\sqrt[{n}]{1-x^{n}}}\mathop {\mathrm {d} x} ={\tfrac {1}{n}}\pi _{n}.}
1
4
π
4
=
1
2
ϖ
.
{\displaystyle {\tfrac {1}{4}}\pi _{4}={\tfrac {1}{\sqrt {2}}}\varpi .}
Euler discovered in 1738 that for the rectangular elastica:[15]
arc
length
⋅
height
=
∫
0
1
d
x
1
−
x
4
⋅
∫
0
1
x
2
d
x
1
−
x
4
=
ϖ
2
⋅
π
2
ϖ
=
π
4
{\displaystyle {\textrm {arc}}\ {\textrm {length}}\cdot {\textrm {height}}=\int _{0}^{1}{\frac {\mathrm {d} x}{\sqrt {1-x^{4}}}}\cdot \int _{0}^{1}{\frac {x^{2}\mathop {\mathrm {d} x} }{\sqrt {1-x^{4}}}}={\frac {\varpi }{2}}\cdot {\frac {\pi }{2\varpi }}={\frac {\pi }{4}}}
Viète's formula for π
2
π
=
1
2
⋅
1
2
+
1
2
1
2
⋅
1
2
+
1
2
1
2
+
1
2
1
2
⋯
{\displaystyle {\frac {2}{\pi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}}}\cdots }
An analogous formula for ϖ [16]
2
ϖ
=
1
2
⋅
1
2
+
1
2
/
1
2
⋅
1
2
+
1
2
/
1
2
+
1
2
/
1
2
⋯
{\displaystyle {\frac {2}{\varpi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\bigg /}\!{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\Bigg /}\!{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\bigg /}\!{\sqrt {\frac {1}{2}}}}}}}\cdots }
The Wallis product for π
π
2
=
∏
n
=
1
∞
(
2
n
2
n
−
1
⋅
2
n
2
n
+
1
)
=
(
2
1
⋅
2
3
)
(
4
3
⋅
4
5
)
(
6
5
⋅
6
7
)
⋯
{\displaystyle {\frac {\pi }{2}}=\prod _{n=1}^{\infty }\left({\frac {2n}{2n-1}}\cdot {\frac {2n}{2n+1}}\right)={\biggl (}{\frac {2}{1}}\cdot {\frac {2}{3}}{\biggr )}{\biggl (}{\frac {4}{3}}\cdot {\frac {4}{5}}{\biggr )}{\biggl (}{\frac {6}{5}}\cdot {\frac {6}{7}}{\biggr )}\cdots }
Analogous formulas for ϖ [17]
ϖ
2
=
∏
n
=
1
∞
(
4
n
2
4
n
2
−
1
⋅
4
n
2
4
n
2
+
1
)
P
Q
{\displaystyle {\frac {\varpi }{2}}=\prod _{n=1}^{\infty }\left({\frac {4n^{2}}{4n^{2}-1}}\cdot {\frac {4n^{2}}{4n^{2}+1}}\right){\frac {P}{Q}}}
ϖ
2
=
∏
n
=
1
∞
(
4
n
−
1
4
n
−
2
⋅
4
n
4
n
+
1
)
=
(
3
2
⋅
4
5
)
(
7
6
⋅
8
9
)
(
11
10
⋅
12
13
)
⋯
{\displaystyle {\frac {\varpi }{2}}=\prod _{n=1}^{\infty }\left({\frac {4n-1}{4n-2}}\cdot {\frac {4n}{4n+1}}\right)={\biggl (}{\frac {3}{2}}\cdot {\frac {4}{5}}{\biggr )}{\biggl (}{\frac {7}{6}}\cdot {\frac {8}{9}}{\biggr )}{\biggl (}{\frac {11}{10}}\cdot {\frac {12}{13}}{\biggr )}\cdots }
where
P
=
∏
(
n
,
k
)
∈
N
+
2
(
4
(
n
+
k
i
)
2
4
(
n
+
k
i
)
2
−
1
⋅
4
(
n
+
k
i
)
2
4
(
n
+
k
i
)
2
+
1
)
,
{\displaystyle P=\prod _{(n,k)\in {\mathbb {N} ^{+}}^{2}}\left({\frac {4(n+ki)^{2}}{4(n+ki)^{2}-1}}\cdot {\frac {4(n+ki)^{2}}{4(n+ki)^{2}+1}}\right),}
Q
=
∏
(
n
,
k
)
∈
N
0
2
(
4
(
n
+
1
/
2
+
(
k
+
1
/
2
)
i
)
2
4
(
n
+
1
/
2
+
(
k
+
1
/
2
)
i
)
2
−
1
⋅
4
(
n
+
1
/
2
+
(
k
+
1
/
2
)
i
)
2
4
(
n
+
1
/
2
+
(
k
+
1
/
2
)
i
)
2
+
1
)
.
{\displaystyle Q=\prod _{(n,k)\in \mathbb {N} _{0}^{2}}\left({\frac {4(n+1/2+(k+1/2)i)^{2}}{4(n+1/2+(k+1/2)i)^{2}-1}}\cdot {\frac {4(n+1/2+(k+1/2)i)^{2}}{4(n+1/2+(k+1/2)i)^{2}+1}}\right).}
A related result is:
ϖ
π
=
∏
n
=
1
∞
(
4
n
−
1
4
n
⋅
4
n
+
2
4
n
+
1
)
=
(
3
4
⋅
6
5
)
(
7
8
⋅
10
9
)
(
11
12
⋅
14
13
)
⋯
{\displaystyle {\frac {\varpi }{\pi }}=\prod _{n=1}^{\infty }\left({\frac {4n-1}{4n}}\cdot {\frac {4n+2}{4n+1}}\right)={\biggl (}{\frac {3}{4}}\cdot {\frac {6}{5}}{\biggr )}{\biggl (}{\frac {7}{8}}\cdot {\frac {10}{9}}{\biggr )}{\biggl (}{\frac {11}{12}}\cdot {\frac {14}{13}}{\biggr )}\cdots }
An infinite series for
ϖ
/
π
{\displaystyle \varpi /\pi }
[18]
ϖ
π
=
∑
n
=
0
∞
(
−
1
)
n
∏
k
=
1
n
(
2
k
−
1
)
2
(
2
k
)
2
=
1
−
1
2
2
2
+
1
2
⋅
3
2
2
2
⋅
4
2
−
1
2
⋅
3
2
⋅
5
2
2
2
⋅
4
2
⋅
6
2
+
⋯
{\displaystyle {\frac {\varpi }{\pi }}=\sum _{n=0}^{\infty }(-1)^{n}\prod _{k=1}^{n}{\frac {(2k-1)^{2}}{(2k)^{2}}}=1-{\frac {1^{2}}{2^{2}}}+{\frac {1^{2}\cdot 3^{2}}{2^{2}\cdot 4^{2}}}-{\frac {1^{2}\cdot 3^{2}\cdot 5^{2}}{2^{2}\cdot 4^{2}\cdot 6^{2}}}+\cdots }
The Machin formula for π
1
4
π
=
4
arctan
1
5
−
arctan
1
239
,
{\textstyle {\tfrac {1}{4}}\pi =4\arctan {\tfrac {1}{5}}-\arctan {\tfrac {1}{239}},}
π
1
4
π
=
arctan
1
2
+
arctan
1
3
{\textstyle {\tfrac {1}{4}}\pi =\arctan {\tfrac {1}{2}}+\arctan {\tfrac {1}{3}}}
ϖ
1
2
ϖ
=
2
arcsl
1
2
+
arcsl
7
23
.
{\displaystyle {\tfrac {1}{2}}\varpi =2\operatorname {arcsl} {\tfrac {1}{2}}+\operatorname {arcsl} {\tfrac {7}{23}}.}
[19]
In a spirit similar to that of the Basel problem ,
∑
z
∈
Z
[
i
]
∖
{
0
}
1
z
4
=
G
4
(
i
)
=
ϖ
4
15
{\displaystyle \sum _{z\in \mathbf {Z} [i]\setminus \{0\}}{\frac {1}{z^{4}}}=G_{4}(i)={\frac {\varpi ^{4}}{15}}}
where
Z
[
i
]
{\displaystyle \mathbf {Z} [i]}
Gaussian integers and
G
4
(
τ
)
{\displaystyle G_{4}(\tau )}
Eisenstein series of weight
4
{\displaystyle 4}
[20]
Zeros, poles and symmetries [ ] At translations of
1
2
ϖ
{\displaystyle {\tfrac {1}{2}}\varpi }
cl and sl are exchanged, and at translations of
1
2
i
ϖ
{\displaystyle {\tfrac {1}{2}}i\varpi }
reciprocated :[21]
cl
(
z
±
1
2
ϖ
)
=
∓
sl
z
,
cl
(
z
±
1
2
i
ϖ
)
=
∓
i
sl
z
sl
(
z
±
1
2
ϖ
)
=
±
cl
z
,
sl
(
z
±
1
2
i
ϖ
)
=
±
i
cl
z
{\displaystyle {\begin{aligned}{\operatorname {cl} }{\bigl (}z\pm {\tfrac {1}{2}}\varpi {\bigr )}&=\mp \operatorname {sl} z,&{\operatorname {cl} }{\bigl (}z\pm {\tfrac {1}{2}}i\varpi {\bigr )}&={\frac {\mp i}{\operatorname {sl} z}}\\[6mu]{\operatorname {sl} }{\bigl (}z\pm {\tfrac {1}{2}}\varpi {\bigr )}&=\pm \operatorname {cl} z,&{\operatorname {sl} }{\bigl (}z\pm {\tfrac {1}{2}}i\varpi {\bigr )}&={\frac {\pm i}{\operatorname {cl} z}}\end{aligned}}}
Doubling these to translations by a unit -Gaussian-integer multiple of
ϖ
{\displaystyle \varpi }
±
ϖ
{\displaystyle \pm \varpi }
±
i
ϖ
{\displaystyle \pm i\varpi }
involution :
cl
(
z
+
ϖ
)
=
cl
(
z
+
i
ϖ
)
=
−
cl
z
sl
(
z
+
ϖ
)
=
sl
(
z
+
i
ϖ
)
=
−
sl
z
{\displaystyle {\begin{aligned}\operatorname {cl} (z+\varpi )&=\operatorname {cl} (z+i\varpi )=-\operatorname {cl} z\\[4mu]\operatorname {sl} (z+\varpi )&=\operatorname {sl} (z+i\varpi )=-\operatorname {sl} z\end{aligned}}}
As a result, both functions are invariant under translation by an even-Gaussian-integer multiple of
ϖ
{\displaystyle \varpi }
[22]
(
a
+
b
i
)
ϖ
,
{\displaystyle (a+bi)\varpi ,}
a
+
b
=
2
k
{\displaystyle a+b=2k}
a b k
cl
(
z
+
(
1
+
i
)
ϖ
)
=
cl
(
z
+
(
1
−
i
)
ϖ
)
=
cl
z
sl
(
z
+
(
1
+
i
)
ϖ
)
=
sl
(
z
+
(
1
−
i
)
ϖ
)
=
sl
z
{\displaystyle {\begin{aligned}{\operatorname {cl} }{\bigl (}z+(1+i)\varpi {\bigr )}&={\operatorname {cl} }{\bigl (}z+(1-i)\varpi {\bigr )}=\operatorname {cl} z\\[4mu]{\operatorname {sl} }{\bigl (}z+(1+i)\varpi {\bigr )}&={\operatorname {sl} }{\bigl (}z+(1-i)\varpi {\bigr )}=\operatorname {sl} z\end{aligned}}}
This makes them elliptic functions (doubly periodic meromorphic functions in the complex plane) with a diagonal square period lattice of fundamental periods
(
1
+
i
)
ϖ
{\displaystyle (1+i)\varpi }
(
1
−
i
)
ϖ
{\displaystyle (1-i)\varpi }
[23]
Reflections and quarter-turn rotations of lemniscate function arguments have simple expressions:
cl
z
¯
=
cl
z
¯
sl
z
¯
=
sl
z
¯
cl
i
z
=
1
cl
z
sl
i
z
=
i
sl
z
{\displaystyle {\begin{aligned}\operatorname {cl} {\bar {z}}&={\overline {\operatorname {cl} z}}\\[6mu]\operatorname {sl} {\bar {z}}&={\overline {\operatorname {sl} z}}\\[4mu]\operatorname {cl} iz&={\frac {1}{\operatorname {cl} z}}\\[6mu]\operatorname {sl} iz&=i\operatorname {sl} z\end{aligned}}}
The sl function has simple zeros at Gaussian integer multiples of ϖ
a
ϖ
+
b
ϖ
i
{\displaystyle a\varpi +b\varpi i}
a b poles at Gaussian half-integer multiples of ϖ
(
a
+
1
2
)
ϖ
+
(
b
+
1
2
)
ϖ
i
{\displaystyle {\bigl (}a+{\tfrac {1}{2}}{\bigr )}\varpi +{\bigl (}b+{\tfrac {1}{2}}{\bigr )}\varpi i}
residues
(
−
1
)
a
−
b
+
1
i
{\displaystyle (-1)^{a-b+1}i}
cl function is reflected and offset from the sl function,
cl
z
=
sl
(
1
2
ϖ
−
z
)
{\displaystyle \operatorname {cl} z={\operatorname {sl} }{\bigl (}{\tfrac {1}{2}}\varpi -z{\bigr )}}
(
a
+
1
2
)
ϖ
+
b
ϖ
i
{\displaystyle {\bigl (}a+{\tfrac {1}{2}}{\bigr )}\varpi +b\varpi i}
a
ϖ
+
(
b
+
1
2
)
ϖ
i
,
{\displaystyle a\varpi +{\bigl (}b+{\tfrac {1}{2}}{\bigr )}\varpi i,}
(
−
1
)
a
−
b
i
.
{\displaystyle (-1)^{a-b}i.}
Since the lemniscate sine is a meromorphic function, it can be written as a ratio of holomorphic functions. Gauss showed that sl has the following product expansion, reflecting the distribution of its zeros and poles:[24]
sl
z
=
M
(
z
)
N
(
z
)
{\displaystyle \operatorname {sl} z={\frac {M(z)}{N(z)}}}
where
M
(
z
)
=
z
∏
α
(
1
−
z
4
/
α
4
)
{\textstyle M(z)=z\prod _{\alpha }(1-z^{4}/\alpha ^{4})}
N
(
z
)
=
∏
β
(
1
−
z
4
/
β
4
)
{\textstyle N(z)=\prod _{\beta }(1-z^{4}/\beta ^{4})}
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
sl which are in the quadrant
Re
z
>
0
,
Im
z
≥
0
{\displaystyle \operatorname {Re} z>0,\operatorname {Im} z\geq 0}
ln
N
(
ϖ
)
=
π
/
2
{\displaystyle \ln N(\varpi )=\pi /2}
[25] [26]
There is also an infinite series reflecting the distribution of the zeros of sl :[27] [28]
1
sl
z
=
∑
(
n
,
k
)
∈
Z
2
(
−
1
)
n
+
k
z
−
(
n
ϖ
+
k
ϖ
i
)
.
{\displaystyle {\frac {1}{\operatorname {sl} z}}=\sum _{(n,k)\in \mathbb {Z} ^{2}}{\frac {(-1)^{n+k}}{z-(n\varpi +k\varpi i)}}.}
Pythagorean-like identity [ ]
Curves
x ² ⊕ y ² = a for various values of
a . Negative
a in green, positive
a in blue,
a = ±1 in red,
a = ∞ in black.
The lemniscate functions satisfy a Pythagorean -like identity:
c
l
2
z
+
s
l
2
z
+
c
l
2
z
s
l
2
z
=
1
{\displaystyle \operatorname {cl^{2}} z+\operatorname {sl^{2}} z+\operatorname {cl^{2}} z\,\operatorname {sl^{2}} z=1}
As a result, the parametric equation
(
x
,
y
)
=
(
cl
t
,
sl
t
)
{\displaystyle (x,y)=(\operatorname {cl} t,\operatorname {sl} t)}
quartic curve
x
2
+
y
2
+
x
2
y
2
=
1.
{\displaystyle x^{2}+y^{2}+x^{2}y^{2}=1.}
This identity can alternately be rewritten:[29]
(
1
+
c
l
2
z
)
(
1
+
s
l
2
z
)
=
2
{\displaystyle {\bigl (}1+\operatorname {cl^{2}} z{\bigr )}{\bigl (}1+\operatorname {sl^{2}} z{\bigr )}=2}
c
l
2
z
=
1
−
s
l
2
z
1
+
s
l
2
z
,
s
l
2
z
=
1
−
c
l
2
z
1
+
c
l
2
z
{\displaystyle \operatorname {cl^{2}} z={\frac {1-\operatorname {sl^{2}} z}{1+\operatorname {sl^{2}} z}},\quad \operatorname {sl^{2}} z={\frac {1-\operatorname {cl^{2}} z}{1+\operatorname {cl^{2}} z}}}
Defining a tangent-sum operator as
a
⊕
b
:=
tan
(
arctan
a
+
arctan
b
)
,
{\displaystyle a\oplus b\mathrel {:=} \tan(\arctan a+\arctan b),}
c
l
2
z
⊕
s
l
2
z
=
1
{\displaystyle \operatorname {cl^{2}} z\oplus \operatorname {sl^{2}} z=1}
Derivatives and integrals [ ] The derivatives are as follows:
d
d
z
cl
z
=
c
l
′
z
=
−
sl
z
(
1
+
c
l
2
z
)
c
l
′
2
z
=
1
−
c
l
4
z
d
d
z
sl
z
=
s
l
′
z
=
cl
z
(
1
+
s
l
2
z
)
s
l
′
2
z
=
1
−
s
l
4
z
{\displaystyle {\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {cl} z=\operatorname {cl'} z&=-\operatorname {sl} z\,{\bigl (}1+\operatorname {cl^{2}} z{\bigr )}\\\operatorname {cl'^{2}} z&=1-\operatorname {cl^{4}} z\\[5mu]{\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {sl} z=\operatorname {sl'} z&=\operatorname {cl} z\,{\bigl (}1+\operatorname {sl^{2}} z{\bigr )}\\\operatorname {sl'^{2}} z&=1-\operatorname {sl^{4}} z\end{aligned}}}
The second derivatives of lemniscate sine and lemniscate cosine are their negative duplicated cubes:
d
2
d
z
2
cl
z
=
−
2
c
l
3
z
{\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} z^{2}}}\operatorname {cl} z=-2\operatorname {cl^{3}} z}
d
2
d
z
2
sl
z
=
−
2
s
l
3
z
{\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} z^{2}}}\operatorname {sl} z=-2\operatorname {sl^{3}} z}
The lemniscate functions can be integrated using the inverse tangent function:
∫
cl
z
d
z
=
arctan
(
sl
z
)
+
C
{\displaystyle \int \operatorname {cl} z\mathop {\mathrm {d} z} =\arctan(\operatorname {sl} z)+C}
∫
sl
z
d
z
=
−
arctan
(
cl
z
)
+
C
{\displaystyle \int \operatorname {sl} z\mathop {\mathrm {d} z} =-\arctan(\operatorname {cl} z)+C}
Argument sum and multiple identities [ ] Like the trigonometric functions, the lemniscate functions satisfy argument sum and difference identities. The original identity used by Fagnano for bisection of the lemniscate was:[30]
sl
(
u
+
v
)
=
sl
u
s
l
′
v
+
sl
v
s
l
′
u
1
+
s
l
2
u
s
l
2
v
{\displaystyle \operatorname {sl} (u+v)={\frac {\operatorname {sl} u\,\operatorname {sl'} v+\operatorname {sl} v\,\operatorname {sl'} u}{1+\operatorname {sl^{2}} u\,\operatorname {sl^{2}} v}}}
The derivative and Pythagorean-like identities can be used to rework the identity used by Fagano in terms of sl and cl . Defining a tangent-sum operator
a
⊕
b
:=
tan
���
(
arctan
a
+
arctan
b
)
{\displaystyle a\oplus b\mathrel {:=} \tan(\arctan a+\arctan b)}
a
⊖
b
:=
a
⊕
(
−
b
)
,
{\displaystyle a\ominus b\mathrel {:=} a\oplus (-b),}
[31]
cl
(
u
+
v
)
=
cl
u
cl
v
⊖
sl
u
sl
v
=
cl
u
cl
v
−
sl
u
sl
v
1
+
sl
u
cl
u
sl
v
cl
v
cl
(
u
−
v
)
=
cl
u
cl
v
⊕
sl
u
sl
v
sl
(
u
+
v
)
=
sl
u
cl
v
⊕
cl
u
sl
v
=
sl
u
cl
v
+
cl
u
sl
v
1
−
sl
u
cl
u
sl
v
cl
v
sl
(
u
−
v
)
=
sl
u
cl
v
⊖
cl
u
sl
v
{\displaystyle {\begin{aligned}\operatorname {cl} (u+v)&=\operatorname {cl} u\,\operatorname {cl} v\ominus \operatorname {sl} u\,\operatorname {sl} v={\frac {\operatorname {cl} u\,\operatorname {cl} v-\operatorname {sl} u\,\operatorname {sl} v}{1+\operatorname {sl} u\,\operatorname {cl} u\,\operatorname {sl} v\,\operatorname {cl} v}}\\[2mu]\operatorname {cl} (u-v)&=\operatorname {cl} u\,\operatorname {cl} v\oplus \operatorname {sl} u\,\operatorname {sl} v\\[2mu]\operatorname {sl} (u+v)&=\operatorname {sl} u\,\operatorname {cl} v\oplus \operatorname {cl} u\,\operatorname {sl} v={\frac {\operatorname {sl} u\,\operatorname {cl} v+\operatorname {cl} u\,\operatorname {sl} v}{1-\operatorname {sl} u\,\operatorname {cl} u\,\operatorname {sl} v\,\operatorname {cl} v}}\\[2mu]\operatorname {sl} (u-v)&=\operatorname {sl} u\,\operatorname {cl} v\ominus \operatorname {cl} u\,\operatorname {sl} v\end{aligned}}}
These resemble their trigonometric analogs :
cos
(
u
±
v
)
=
cos
u
cos
v
∓
sin
u
sin
v
sin
(
u
±
v
)
=
sin
u
cos
v
±
cos
u
sin
v
{\displaystyle {\begin{aligned}\cos(u\pm v)&=\cos u\,\cos v\mp \sin u\,\sin v\\[6mu]\sin(u\pm v)&=\sin u\,\cos v\pm \cos u\,\sin v\end{aligned}}}
Bisection formulas:
cl
2
1
2
x
=
1
+
cl
x
1
+
sl
2
x
1
+
sl
2
x
+
1
{\displaystyle \operatorname {cl} ^{2}{\tfrac {1}{2}}x={\frac {1+\operatorname {cl} x{\sqrt {1+\operatorname {sl} ^{2}x}}}{{\sqrt {1+\operatorname {sl} ^{2}x}}+1}}}
sl
2
1
2
x
=
1
−
cl
x
1
+
sl
2
x
1
+
sl
2
x
+
1
{\displaystyle \operatorname {sl} ^{2}{\tfrac {1}{2}}x={\frac {1-\operatorname {cl} x{\sqrt {1+\operatorname {sl} ^{2}x}}}{{\sqrt {1+\operatorname {sl} ^{2}x}}+1}}}
[32]
cl
2
x
=
−
1
+
2
cl
2
x
+
cl
4
x
1
+
2
cl
2
x
−
cl
4
x
{\displaystyle \operatorname {cl} 2x={\frac {-1+2\,\operatorname {cl} ^{2}x+\operatorname {cl} ^{4}x}{1+2\,\operatorname {cl} ^{2}x-\operatorname {cl} ^{4}x}}}
sl
2
x
=
2
sl
x
cl
x
1
+
sl
2
x
1
+
sl
4
x
{\displaystyle \operatorname {sl} 2x=2\,\operatorname {sl} x\,\operatorname {cl} x{\frac {1+\operatorname {sl} ^{2}x}{1+\operatorname {sl} ^{4}x}}}
Triplication formulas:[32]
cl
3
x
=
−
3
cl
x
+
6
cl
5
x
+
cl
9
x
1
+
6
cl
4
x
−
3
cl
8
x
{\displaystyle \operatorname {cl} 3x={\frac {-3\,\operatorname {cl} x+6\,\operatorname {cl} ^{5}x+\operatorname {cl} ^{9}x}{1+6\,\operatorname {cl} ^{4}x-3\,\operatorname {cl} ^{8}x}}}
sl
3
x
=
3
sl
x
−
6
sl
5
x
−
sl
9
x
1
+
6
sl
4
x
−
3
sl
8
x
{\displaystyle \operatorname {sl} 3x={\frac {3\,\operatorname {sl} x-6\,\operatorname {sl} ^{5}x-\operatorname {sl} ^{9}x}{1+6\,\operatorname {sl} ^{4}x-3\,\operatorname {sl} ^{8}x}}}
Specific values [ ] Just as for the trigonometric functions, values of the lemniscate functions can be computed for divisions of the lemniscate into n n
n
=
2
k
p
1
p
2
⋯
p
m
{\displaystyle n=2^{k}p_{1}p_{2}\cdots p_{m}}
k m integers and each p i Fermat prime .[33] n
(
x
2
+
y
2
)
2
=
x
2
−
y
2
{\displaystyle (x^{2}+y^{2})^{2}=x^{2}-y^{2}}
n n ≤ 20n
(
x
2
+
y
2
)
2
=
x
2
−
y
2
{\displaystyle (x^{2}+y^{2})^{2}=x^{2}-y^{2}}
x
2
+
y
2
=
sl
2
2
j
ϖ
n
{\displaystyle x^{2}+y^{2}=\operatorname {sl} ^{2}{\tfrac {2j\varpi }{n}}}
j
∈
{
1
,
2
,
…
,
n
}
{\displaystyle j\in \{1,2,\ldots ,n\}}
n
{\displaystyle n}
cl
2
ϖ
n
{\displaystyle \operatorname {cl} {\tfrac {2\varpi }{n}}}
sl
2
ϖ
n
{\displaystyle \operatorname {sl} {\tfrac {2\varpi }{n}}}
2
{\displaystyle 2}
−
1
{\displaystyle -1}
0
{\displaystyle 0}
4
{\displaystyle 4}
0
{\displaystyle 0}
1
{\displaystyle 1}
5
{\displaystyle 5}
1
2
(
5
4
−
1
)
(
5
+
2
−
1
)
{\displaystyle {\tfrac {1}{2}}({\sqrt[{4}]{5}}-1)\left({\sqrt {{\sqrt {5}}+2}}-1\right)}
1
2
2
4
(
5
−
1
)
20
4
+
5
−
1
{\displaystyle {\tfrac {1}{2{\sqrt[{4}]{2}}}}({\sqrt {5}}-1){\sqrt {{\sqrt[{4}]{20}}+{\sqrt {{\sqrt {5}}-1}}}}}
6
{\displaystyle 6}
1
2
(
3
+
1
−
12
4
)
{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt {3}}+1-{\sqrt[{4}]{12}}{\bigr )}}
2
3
−
3
4
{\displaystyle {\sqrt[{4}]{2{\sqrt {3}}-3}}}
8
{\displaystyle 8}
2
−
1
{\displaystyle {\sqrt {{\sqrt {2}}-1}}}
2
−
1
{\displaystyle {\sqrt {{\sqrt {2}}-1}}}
10
{\displaystyle 10}
1
2
(
5
4
−
1
)
(
5
+
2
+
1
)
{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt[{4}]{5}}-1{\bigr )}{\Bigl (}{\sqrt {{\sqrt {5}}+2}}+1{\Bigr )}}
1
2
5
−
2
4
2
(
5
−
5
)
+
1
−
5
{\displaystyle {\tfrac {1}{\sqrt {2}}}{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {{\sqrt {2{\bigl (}5-{\sqrt {5}}{\bigr )}}}+1-{\sqrt {5}}}}}
12
{\displaystyle 12}
2
3
−
3
4
{\displaystyle {\sqrt[{4}]{2{\sqrt {3}}-3}}}
1
2
(
3
+
1
−
12
4
)
{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt {3}}+1-{\sqrt[{4}]{12}}{\bigr )}}
16
{\displaystyle 16}
(
2
4
−
1
)
(
2
+
1
+
2
+
2
)
{\displaystyle {\sqrt {{\bigl (}{\sqrt[{4}]{2}}-1{\bigr )}{\Bigl (}{\sqrt {2}}+1+{\sqrt {2+{\sqrt {2}}}}{\Bigr )}}}}
(
2
4
−
1
)
(
2
+
1
−
2
+
2
)
{\displaystyle {\sqrt {{\bigl (}{\sqrt[{4}]{2}}-1{\bigr )}{\Bigl (}{\sqrt {2}}+1-{\sqrt {2+{\sqrt {2}}}}{\Bigr )}}}}
20
{\displaystyle 20}
1
2
5
−
2
4
2
(
5
−
5
)
−
1
+
5
{\displaystyle {\tfrac {1}{\sqrt {2}}}{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {{\sqrt {2{\bigl (}5-{\sqrt {5}}{\bigr )}}}-1+{\sqrt {5}}}}}
1
2
(
5
4
−
1
)
(
5
+
2
−
1
)
{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt[{4}]{5}}-1{\bigr )}{\Bigl (}{\sqrt {{\sqrt {5}}+2}}-1{\Bigr )}}
Power series [ ] The power series expansion of the lemniscate sine at the origin is[34]
sl
z
=
∑
n
=
0
∞
a
n
z
n
=
z
−
1
10
z
5
+
1
120
z
9
−
11
15600
z
13
+
⋯
,
z
∈
C
,
|
z
|
<
ϖ
2
{\displaystyle \operatorname {sl} z=\sum _{n=0}^{\infty }a_{n}z^{n}=z-{\tfrac {1}{10}}z^{5}+{\tfrac {1}{120}}z^{9}-{\tfrac {11}{15600}}z^{13}+\cdots ,\quad z\in \mathbb {C} ,\,|z|<{\tfrac {\varpi }{\sqrt {2}}}}
where the coefficients
a
n
{\displaystyle a_{n}}
n
≢
1
(
mod
4
)
⟹
a
n
=
0
,
{\displaystyle n\not \equiv 1{\pmod {4}}\implies a_{n}=0,}
a
1
=
1
,
∀
n
∈
N
0
:
a
n
+
2
=
−
2
(
n
+
1
)
(
n
+
2
)
∑
i
+
j
+
k
=
n
a
i
a
j
a
k
{\displaystyle a_{1}=1,\,\forall n\in \mathbb {N} _{0}:\,a_{n+2}=-{\frac {2}{(n+1)(n+2)}}\sum _{i+j+k=n}a_{i}a_{j}a_{k}}
where
i
+
j
+
k
=
n
{\displaystyle i+j+k=n}
compositions of
n
{\displaystyle n}
a
13
{\displaystyle a_{13}}
13
−
2
=
11
{\displaystyle 13-2=11}
11
=
9
+
1
+
1
=
1
+
9
+
1
=
1
+
1
+
9
{\displaystyle 11=9+1+1=1+9+1=1+1+9}
11
=
5
+
5
+
1
=
5
+
1
+
5
=
1
+
5
+
5
{\displaystyle 11=5+5+1=5+1+5=1+5+5}
a
13
=
−
2
12
⋅
13
(
a
9
a
1
a
1
+
a
1
a
9
a
1
+
a
1
a
1
a
9
+
a
5
a
5
a
1
+
a
5
a
1
a
5
+
a
1
a
5
a
5
)
=
−
11
15600
.
{\displaystyle a_{13}=-{\tfrac {2}{12\cdot 13}}(a_{9}a_{1}a_{1}+a_{1}a_{9}a_{1}+a_{1}a_{1}a_{9}+a_{5}a_{5}a_{1}+a_{5}a_{1}a_{5}+a_{1}a_{5}a_{5})=-{\tfrac {11}{15600}}.}
Relation to Weierstrass and Jacobi elliptic functions [ ] The lemniscate functions are closely related to the Weierstrass elliptic function
℘
(
z
;
1
,
0
)
{\displaystyle \wp (z;1,0)}
g 2 = 1g 3 = 0
ω
1
=
2
ϖ
,
{\displaystyle \omega _{1}={\sqrt {2}}\varpi ,}
ω
2
=
i
ω
1
{\displaystyle \omega _{2}=i\omega _{1}}
e
1
=
1
2
,
e
2
=
0
,
e
3
=
−
1
2
.
{\displaystyle e_{1}={\tfrac {1}{2}},\ e_{2}=0,\ e_{3}=-{\tfrac {1}{2}}.}
The related case of a Weierstrass elliptic function with g 2 = a g 3 = 0a > 0a < 0parallelogram is either a square or a rhombus . The Weierstrass elliptic function
℘
(
z
;
−
1
,
0
)
{\displaystyle \wp (z;-1,0)}
[35]
The square of the lemniscate sine can be represented as
sl
2
z
=
1
℘
(
z
;
4
,
0
)
=
i
2
℘
(
(
1
−
i
)
z
;
−
1
,
0
)
=
−
2
℘
(
2
z
+
(
i
−
1
)
ϖ
2
;
1
,
0
)
{\displaystyle \operatorname {sl} ^{2}z={\frac {1}{\wp (z;4,0)}}={\frac {i}{2\wp ((1-i)z;-1,0)}}={-2\wp }{\left({\sqrt {2}}z+(i-1){\frac {\varpi }{\sqrt {2}}};1,0\right)}}
where the second and third argument of
℘
{\displaystyle \wp }
g 2 g 3
sl
2
z
=
ϖ
2
℘
(
z
/
ϖ
,
i
)
{\displaystyle \operatorname {sl} ^{2}z={\frac {\varpi ^{2}}{\wp (z/\varpi ,i)}}}
where the second argument of
℘
{\displaystyle \wp }
τ
{\displaystyle \tau }
rational function in the Weierstrass elliptic function and its derivative:[36]
sl
z
=
−
2
℘
(
(
1
+
i
)
z
;
1
/
4
,
0
)
℘
′
(
(
1
+
i
)
z
;
1
/
4
,
0
)
{\displaystyle \operatorname {sl} z=-2{\frac {\wp ((1+i)z;1/4,0)}{\wp '((1+i)z;1/4,0)}}}
where the second and third argument of
℘
{\displaystyle \wp }
g 2 g 3
τ
{\displaystyle \tau }
sl
z
=
−
2
℘
(
(
1
+
i
)
z
/
(
2
ϖ
)
,
i
)
℘
′
(
(
1
+
i
)
z
/
(
2
ϖ
)
,
i
)
.
{\displaystyle \operatorname {sl} z=-2{\frac {\wp ((1+i)z/(2\varpi ),i)}{\wp '((1+i)z/(2\varpi ),i)}}.}
The lemniscate functions can also be written in terms of Jacobi elliptic functions . The Jacobi elliptic functions
sn
{\displaystyle \operatorname {sn} }
cd
{\displaystyle \operatorname {cd} }
sn
{\displaystyle \operatorname {sn} }
cd
{\displaystyle \operatorname {cd} }
i
sd
{\displaystyle \operatorname {sd} }
cn
{\displaystyle \operatorname {cn} }
1
/
2
{\displaystyle 1/{\sqrt {2}}}
[37]
sl
z
=
sn
(
z
;
i
)
=
1
2
sd
(
2
z
;
1
2
)
{\displaystyle \operatorname {sl} z=\operatorname {sn} (z;i)={{\tfrac {1}{\sqrt {2}}}\operatorname {sd} }\left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right)}
cl
z
=
cd
(
z
;
i
)
=
cn
(
2
z
;
1
2
)
{\displaystyle \operatorname {cl} z=\operatorname {cd} (z;i)={\operatorname {cn} }\left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right)}
where the second arguments denote the elliptic modulus.
Relation to the modular lambda function [ ] The lemniscate sine can be used for the computation of values of the modular lambda function :
∏
k
=
1
n
sl
(
2
k
−
1
2
n
+
1
ϖ
2
)
=
λ
(
(
2
n
+
1
)
i
)
1
−
λ
(
(
2
n
+
1
)
i
)
8
{\displaystyle \prod _{k=1}^{n}\;{\operatorname {sl} }{\left({\frac {2k-1}{2n+1}}{\frac {\varpi }{2}}\right)}={\sqrt[{8}]{\frac {\lambda ((2n+1)i)}{1-\lambda ((2n+1)i)}}}}
For example:
sl
(
1
14
ϖ
)
sl
(
3
14
ϖ
)
sl
(
5
14
ϖ
)
=
λ
(
7
i
)
1
−
λ
(
7
i
)
8
=
tan
(
1
2
arccsc
(
1
2
8
7
+
21
+
1
2
7
+
1
)
)
sl
(
1
18
ϖ
)
sl
(
3
18
ϖ
)
sl
(
5
18
ϖ
)
sl
(
7
18
ϖ
)
=
λ
(
9
i
)
1
−
λ
(
9
i
)
8
=
tan
(
π
4
−
arctan
(
2
2
3
−
2
3
−
2
2
−
3
3
+
3
−
1
12
4
)
)
{\displaystyle {\begin{aligned}&{\operatorname {sl} }{\bigl (}{\tfrac {1}{14}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {3}{14}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {5}{14}}\varpi {\bigr )}\\[7mu]&\quad {}={\sqrt[{8}]{\frac {\lambda (7i)}{1-\lambda (7i)}}}={\tan }{\Bigl (}{{\tfrac {1}{2}}\operatorname {arccsc} }{\Bigl (}{\tfrac {1}{2}}{\sqrt {8{\sqrt {7}}+21}}+{\tfrac {1}{2}}{\sqrt {7}}+1{\Bigr )}{\Bigr )}\\[18mu]&{\operatorname {sl} }{\bigl (}{\tfrac {1}{18}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {3}{18}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {5}{18}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {7}{18}}\varpi {\bigr )}\\[-3mu]&\quad {}={\sqrt[{8}]{\frac {\lambda (9i)}{1-\lambda (9i)}}}={\tan }{\Biggl (}{\frac {\pi }{4}}-{\arctan }{\Biggl (}{\frac {2{\sqrt[{3}]{2{\sqrt {3}}-2}}-2{\sqrt[{3}]{2-{\sqrt {3}}}}+{\sqrt {3}}-1}{\sqrt[{4}]{12}}}{\Biggr )}{\Biggr )}\end{aligned}}}
Methods of computation [ ] Several methods of computing
sl
x
{\displaystyle \operatorname {sl} x}
π
x
=
ϖ
x
~
{\displaystyle \pi x=\varpi {\tilde {x}}}
sl
(
ϖ
x
~
/
π
)
.
{\displaystyle \operatorname {sl} (\varpi {\tilde {x}}/\pi ).}
A hyperbolic series method:[40] [27] [41] [42]
sl
(
ϖ
π
x
)
=
π
ϖ
∑
n
=
−
∞
∞
(
−
1
)
n
cosh
(
x
−
(
n
+
1
/
2
)
π
)
{\displaystyle \operatorname {sl} \left({\frac {\varpi }{\pi }}x\right)={\frac {\pi }{\varpi }}\sum _{n=-\infty }^{\infty }{\frac {(-1)^{n}}{\cosh(x-(n+1/2)\pi )}}}
1
sl
(
ϖ
x
/
π
)
=
π
ϖ
∑
n
=
−
∞
∞
(
−
1
)
n
sinh
(
x
−
n
π
)
=
π
ϖ
∑
n
=
−
∞
∞
(
−
1
)
n
sin
(
x
−
n
π
i
)
{\displaystyle {\frac {1}{\operatorname {sl} (\varpi x/\pi )}}={\frac {\pi }{\varpi }}\sum _{n=-\infty }^{\infty }{\frac {(-1)^{n}}{{\sinh }{\left(x-n\pi \right)}}}={\frac {\pi }{\varpi }}\sum _{n=-\infty }^{\infty }{\frac {(-1)^{n}}{\sin(x-n\pi i)}}}
Fourier series method:[43]
sl
(
ϖ
π
x
)
=
2
π
ϖ
∑
n
=
0
∞
(
−
1
)
n
sin
(
(
2
n
+
1
)
x
)
cosh
(
(
n
+
1
/
2
)
π
)
,
|
Im
x
|
<
π
2
{\displaystyle \operatorname {sl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}={\frac {2\pi }{\varpi }}\sum _{n=0}^{\infty }{\frac {(-1)^{n}\sin((2n+1)x)}{\cosh((n+1/2)\pi )}},\quad \left|\operatorname {Im} x\right|<{\frac {\pi }{2}}}
The lemniscate sine can be computed more rapidly by
sl
(
ϖ
π
x
)
=
θ
1
(
x
,
e
−
π
)
θ
3
(
x
,
e
−
π
)
{\displaystyle \operatorname {sl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}={\frac {{\theta _{1}}{\left(x,e^{-\pi }\right)}}{{\theta _{3}}{\left(x,e^{-\pi }\right)}}}}
where
θ
1
(
x
,
q
)
=
∑
n
∈
Z
(
−
1
)
n
q
(
n
+
1
/
2
)
2
sin
(
(
2
n
+
1
)
x
)
,
θ
3
(
x
,
q
)
=
∑
n
∈
Z
q
n
2
cos
2
n
x
{\displaystyle {\begin{aligned}\theta _{1}(x,q)&=\sum _{n\in \mathbb {Z} }(-1)^{n}q^{(n+1/2)^{2}}\sin((2n+1)x),\\\theta _{3}(x,q)&=\sum _{n\in \mathbb {Z} }q^{n^{2}}\cos 2nx\end{aligned}}}
are the Jacobi theta functions .[44]
Two other fast computation methods use the following sum and product series:
sl
(
ϖ
π
x
)
=
f
(
4
π
ϖ
sin
(
x
)
∑
n
=
1
∞
cosh
[
(
2
n
−
1
)
π
]
cosh
[
(
2
n
−
1
)
π
]
2
−
cos
(
x
)
2
)
{\displaystyle {\text{sl}}{\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=f{\biggl (}{\frac {4\pi }{\varpi }}\sin(x)\sum _{n=1}^{\infty }{\frac {\cosh[(2n-1)\pi ]}{\cosh[(2n-1)\pi ]^{2}-\cos(x)^{2}}}{\biggr )}}
cl
(
ϖ
π
x
)
=
f
(
4
π
ϖ
cos
(
x
)
∑
n
=
1
∞
cosh
[
(
2
n
−
1
)
π
]
cosh
[
(
2
n
−
1
)
π
]
2
−
sin
(
x
)
2
)
{\displaystyle {\text{cl}}{\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=f{\biggl (}{\frac {4\pi }{\varpi }}\cos(x)\sum _{n=1}^{\infty }{\frac {\cosh[(2n-1)\pi ]}{\cosh[(2n-1)\pi ]^{2}-\sin(x)^{2}}}{\biggr )}}
s
l
(
ϖ
π
x
)
=
2
exp
(
−
1
4
π
)
sin
(
x
)
∏
n
=
1
∞
1
−
2
cos
(
2
x
)
exp
(
−
2
n
π
)
+
exp
(
−
4
n
π
)
1
+
2
cos
(
2
x
)
exp
[
−
(
2
n
−
1
)
π
]
+
exp
[
−
(
4
n
−
2
)
π
]
{\displaystyle \mathrm {sl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=2\exp {\bigl (}{-{\tfrac {1}{4}}\pi }{\bigr )}\sin(x)\prod _{n=1}^{\infty }{\frac {1-2\cos(2x)\exp(-2n\pi )+\exp(-4n\pi )}{1+2\cos(2x)\exp[-(2n-1)\pi ]+\exp[-(4n-2)\pi ]}}}
c
l
(
ϖ
π
x
)
=
2
exp
(
−
1
4
π
)
cos
(
x
)
∏
n
=
1
∞
1
+
2
cos
(
2
x
)
exp
(
−
2
n
π
)
+
exp
(
−
4
n
π
)
1
−
2
cos
(
2
x
)
exp
[
−
(
2
n
−
1
)
π
]
+
exp
[
−
(
4
n
−
2
)
π
]
{\displaystyle \mathrm {cl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=2\exp {\bigl (}{-{\tfrac {1}{4}}\pi }{\bigr )}\cos(x)\prod _{n=1}^{\infty }{\frac {1+2\cos(2x)\exp(-2n\pi )+\exp(-4n\pi )}{1-2\cos(2x)\exp[-(2n-1)\pi ]+\exp[-(4n-2)\pi ]}}}
where
f
(
x
)
=
tan
(
2
arctan
x
)
=
2
x
/
(
1
−
x
2
)
.
{\displaystyle f(x)=\tan(2\arctan x)=2x/(1-x^{2}).}
The following series identities were discovered by Ramanujan :[45]
ϖ
2
π
2
sl
2
(
ϖ
x
/
π
)
=
1
sin
2
x
−
1
π
−
8
∑
n
=
1
∞
n
cos
2
n
x
e
2
n
π
−
1
{\displaystyle {\frac {\varpi ^{2}}{\pi ^{2}\operatorname {sl} ^{2}(\varpi x/\pi )}}={\frac {1}{\sin ^{2}x}}-{\frac {1}{\pi }}-8\sum _{n=1}^{\infty }{\frac {n\cos 2nx}{e^{2n\pi }-1}}}
arctan
sl
(
ϖ
π
x
)
=
2
∑
n
=
0
∞
sin
(
(
2
n
+
1
)
x
)
(
2
n
+
1
)
cosh
(
(
n
+
1
/
2
)
π
)
{\displaystyle \arctan \operatorname {sl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=2\sum _{n=0}^{\infty }{\frac {\sin((2n+1)x)}{(2n+1)\cosh((n+1/2)\pi )}}}
Inverse functions [ ] The inverse function of the lemniscate sine is the lemniscate arcsine, defined as:
arcsl
x
=
∫
0
x
1
1
−
t
4
d
t
{\displaystyle \operatorname {arcsl} x=\int _{0}^{x}{\frac {1}{\sqrt {1-t^{4}}}}\mathrm {d} t}
The inverse function of the lemniscate cosine is the lemniscate arccosine. This function is defined by following expression:
arccl
x
=
∫
x
1
1
1
−
t
4
d
t
=
1
2
ϖ
−
arcsl
x
{\displaystyle \operatorname {arccl} x=\int _{x}^{1}{\frac {1}{\sqrt {1-t^{4}}}}\mathrm {d} t={\tfrac {1}{2}}\varpi -\operatorname {arcsl} x}
For x
−
1
≤
x
≤
1
{\displaystyle -1\leq x\leq 1}
sl
(
arcsl
x
)
=
x
{\displaystyle \operatorname {sl} (\operatorname {arcsl} x)=x}
cl
(
arccl
x
)
=
x
{\displaystyle \operatorname {cl} (\operatorname {arccl} x)=x}
For the halving of the lemniscate arc length these formulas are valid:
sl
(
1
2
arcsl
x
)
=
sin
(
1
2
arcsin
x
)
sech
(
1
2
arsinh
x
)
sl
(
1
2
arcsl
x
)
2
=
tan
(
1
4
arcsin
x
2
)
{\displaystyle {\begin{aligned}{\operatorname {sl} }{\bigl (}{\tfrac {1}{2}}\operatorname {arcsl} x{\bigr )}&={\sin }{\bigl (}{\tfrac {1}{2}}\arcsin x{\bigr )}\,{\operatorname {sech} }{\bigl (}{\tfrac {1}{2}}\operatorname {arsinh} x{\bigr )}\\{\operatorname {sl} }{\bigl (}{\tfrac {1}{2}}\operatorname {arcsl} x{\bigr )}^{2}&={\tan }{\bigl (}{\tfrac {1}{4}}\arcsin x^{2}{\bigr )}\end{aligned}}}
Expression using elliptic integrals [ ] The lemniscate arcsine and the lemniscate arccosine can also be expressed by the Legendre-Form:
These functions can be displayed directly by using the incomplete elliptic integral of the first kind:
arcsl
x
=
1
2
F
[
arcsin
(
2
x
1
+
x
2
)
;
1
2
]
{\displaystyle \operatorname {arcsl} x={\frac {1}{\sqrt {2}}}F\left[{\arcsin }{\left({\frac {{\sqrt {2}}x}{\sqrt {1+x^{2}}}}\right)};{\frac {1}{\sqrt {2}}}\right]}
arcsl
x
=
2
(
2
−
1
)
F
[
arcsin
[
(
2
+
1
)
x
1
+
x
2
+
1
]
;
(
2
−
1
)
2
]
{\displaystyle \operatorname {arcsl} x=2({\sqrt {2}}-1)F\left[{\arcsin }{\left[{\frac {({\sqrt {2}}+1)x}{{\sqrt {1+x^{2}}}+1}}\right]};({\sqrt {2}}-1)^{2}\right]}
The arc lengths of the lemniscate can also be expressed by only using the arc lengths of ellipses (calculated by elliptic integrals of the second kind):
arcsl
x
=
2
+
2
2
E
[
arcsin
[
(
2
+
1
)
x
1
+
x
2
+
1
]
;
(
2
−
1
)
2
]
−
E
[
arcsin
(
2
x
1
+
x
2
)
;
1
2
]
+
x
1
−
x
2
2
(
1
+
x
2
+
1
+
x
2
)
{\displaystyle {\begin{aligned}\operatorname {arcsl} x={}&{\frac {2+{\sqrt {2}}}{2}}E\left[{\arcsin }{\left[{\frac {({\sqrt {2}}+1)x}{{\sqrt {1+x^{2}}}+1}}\right]};({\sqrt {2}}-1)^{2}\right]\\[5mu]&\ \ -E\left[{\arcsin }{\left({\frac {{\sqrt {2}}x}{\sqrt {1+x^{2}}}}\right)};{\frac {1}{\sqrt {2}}}\right]+{\frac {x{\sqrt {1-x^{2}}}}{{\sqrt {2}}(1+x^{2}+{\sqrt {1+x^{2}}})}}\end{aligned}}}
The lemniscate arccosine has this expression:
arccl
x
=
1
2
F
[
arccos
x
;
1
2
]
{\displaystyle \operatorname {arccl} x={\frac {1}{\sqrt {2}}}F\left[\arccos x;{\frac {1}{\sqrt {2}}}\right]}
Use in integration [ ] The lemniscate can be used to integrate many functions. Here is a list of important integrals (the constants of integration are omitted):
∫
1
1
−
x
4
d
x
=
arcsl
x
{\displaystyle \int {\frac {1}{\sqrt {1-x^{4}}}}\,\mathrm {d} x=\operatorname {arcsl} x}
∫
1
(
x
2
+
1
)
(
2
x
2
+
1
)
d
x
=
arcsl
(
x
x
2
+
1
)
{\displaystyle \int {\frac {1}{\sqrt {(x^{2}+1)(2x^{2}+1)}}}\,\mathrm {d} x={\operatorname {arcsl} }{\left({\frac {x}{\sqrt {x^{2}+1}}}\right)}}
∫
1
x
4
+
6
x
2
+
1
d
x
=
arcsl
(
2
x
x
4
+
6
x
2
+
1
+
x
2
+
1
)
{\displaystyle \int {\frac {1}{\sqrt {x^{4}+6x^{2}+1}}}\,\mathrm {d} x={\operatorname {arcsl} }{\left({\frac {{\sqrt {2}}x}{\sqrt {{\sqrt {x^{4}+6x^{2}+1}}+x^{2}+1}}}\right)}}
∫
1
x
4
+
1
d
x
=
2
arcsl
(
x
x
4
+
1
+
1
)
{\displaystyle \int {\frac {1}{\sqrt {x^{4}+1}}}\,\mathrm {d} x={{\sqrt {2}}\operatorname {arcsl} }{\left({\frac {x}{\sqrt {{\sqrt {x^{4}+1}}+1}}}\right)}}
∫
1
(
1
−
x
4
)
3
4
d
x
=
2
arcsl
(
x
1
+
1
−
x
4
)
{\displaystyle \int {\frac {1}{\sqrt[{4}]{(1-x^{4})^{3}}}}\,\mathrm {d} x={{\sqrt {2}}\operatorname {arcsl} }{\left({\frac {x}{\sqrt {1+{\sqrt {1-x^{4}}}}}}\right)}}
∫
1
(
x
4
+
1
)
3
4
d
x
=
arcsl
(
x
x
4
+
1
4
)
{\displaystyle \int {\frac {1}{\sqrt[{4}]{(x^{4}+1)^{3}}}}\,\mathrm {d} x={\operatorname {arcsl} }{\left({\frac {x}{\sqrt[{4}]{x^{4}+1}}}\right)}}
∫
1
(
1
−
x
2
)
3
4
d
x
=
2
arcsl
(
x
1
+
1
−
x
2
)
{\displaystyle \int {\frac {1}{\sqrt[{4}]{(1-x^{2})^{3}}}}\,\mathrm {d} x={2\operatorname {arcsl} }{\left({\frac {x}{1+{\sqrt {1-x^{2}}}}}\right)}}
∫
1
(
x
2
+
1
)
3
4
d
x
=
2
arcsl
(
x
x
2
+
1
+
1
)
{\displaystyle \int {\frac {1}{\sqrt[{4}]{(x^{2}+1)^{3}}}}\,\mathrm {d} x={2\operatorname {arcsl} }{\left({\frac {x}{{\sqrt {x^{2}+1}}+1}}\right)}}
∫
1
(
a
x
2
+
b
x
+
c
)
3
4
d
x
=
2
2
4
a
2
c
−
a
b
2
4
arcsl
(
2
a
x
+
b
4
a
(
a
x
2
+
b
x
+
c
)
+
4
a
c
−
b
2
)
{\displaystyle \int {\frac {1}{\sqrt[{4}]{(ax^{2}+bx+c)^{3}}}}\,\mathrm {d} x={{\frac {2{\sqrt {2}}}{\sqrt[{4}]{4a^{2}c-ab^{2}}}}\operatorname {arcsl} }{\left({\frac {2ax+b}{{\sqrt {4a(ax^{2}+bx+c)}}+{\sqrt {4ac-b^{2}}}}}\right)}}
∫
sech
x
d
x
=
2
arcsl
(
tanh
1
2
x
)
{\displaystyle \int {\sqrt {\operatorname {sech} x}}\,\mathrm {d} x={2\operatorname {arcsl} }{\bigl (}\tanh {\tfrac {1}{2}}x{\bigr )}}
∫
sec
x
d
x
=
2
arcsl
(
tan
1
2
x
)
{\displaystyle \int {\sqrt {\sec x}}\,\mathrm {d} x={2\operatorname {arcsl} }{\bigl (}\tan {\tfrac {1}{2}}x{\bigr )}}
Hyperbolic lemniscate functions [ ]
The hyperbolic lemniscate sine (red) and hyperbolic lemniscate cosine (purple) applied to a real argument, in comparison with the trigonometric tangent (pale dashed red).
The hyperbolic lemniscate sine (slh ) and cosine (clh ) can be defined by their inverse functions as follows:
z
=
∫
0
slh
z
d
t
1
+
t
4
=
∫
clh
z
∞
d
t
1
+
t
4
{\displaystyle z=\int _{0}^{\operatorname {slh} z}{\frac {\mathrm {d} t}{\sqrt {1+t^{4}}}}=\int _{\operatorname {clh} z}^{\infty }{\frac {\mathrm {d} t}{\sqrt {1+t^{4}}}}}
The complete integral has the value:
∫
0
∞
d
t
t
4
+
1
=
1
4
B
(
1
4
,
1
4
)
=
1
2
ϖ
=
1.85407
46773
01371
…
{\displaystyle \int _{0}^{\infty }{\frac {\mathrm {d} t}{\sqrt {t^{4}+1}}}={\tfrac {1}{4}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{4}}{\bigr )}={\tfrac {1}{\sqrt {2}}}\varpi =1.85407\;46773\;01371\ldots }
Therefore, the two defined functions have following relation to each other:
slh
z
=
clh
(
1
2
ϖ
−
z
)
{\displaystyle \operatorname {slh} z={\operatorname {clh} }{{\Bigl (}{\tfrac {1}{\sqrt {2}}}\varpi -z{\Bigr )}}}
The product of hyperbolic lemniscate sine and hyperbolic lemniscate cosine is equal to one:
slh
z
clh
z
=
1
{\displaystyle \operatorname {slh} z\,\operatorname {clh} z=1}
The hyperbolic lemniscate functions can be expressed in terms of lemniscate sine and lemniscate cosine:
slh
(
2
x
)
=
(
1
+
cl
2
x
)
sl
x
2
cl
x
{\displaystyle \operatorname {slh} {\bigl (}{\sqrt {2}}x{\bigr )}={\frac {(1+\operatorname {cl} ^{2}x)\operatorname {sl} x}{{\sqrt {2}}\operatorname {cl} x}}}
clh
(
2
x
)
=
(
1
+
sl
2
x
)
cl
x
2
sl
x
{\displaystyle \operatorname {clh} {\bigl (}{\sqrt {2}}x{\bigr )}={\frac {(1+\operatorname {sl} ^{2}x)\operatorname {cl} x}{{\sqrt {2}}\operatorname {sl} x}}}
But there is also a relation to the Jacobi elliptic functions with the elliptic modulus one by square root of two:
slh
x
=
sn
(
x
;
1
/
2
)
cd
(
x
;
1
/
2
)
{\displaystyle \operatorname {slh} x={\frac {\operatorname {sn} (x;1/{\sqrt {2}})}{\operatorname {cd} (x;1/{\sqrt {2}})}}}
clh
x
=
cd
(
x
;
1
/
2
)
sn
(
x
;
1
/
2
)
{\displaystyle \operatorname {clh} x={\frac {\operatorname {cd} (x;1/{\sqrt {2}})}{\operatorname {sn} (x;1/{\sqrt {2}})}}}
The hyperbolic lemniscate sine has following imaginary relation to the lemniscate sine:
slh
z
=
1
−
i
2
sl
(
1
+
i
2
z
)
=
sl
(
−
1
4
z
)
−
1
4
{\displaystyle \operatorname {slh} z={\frac {1-i}{\sqrt {2}}}\operatorname {sl} \left({\frac {1+i}{\sqrt {2}}}z\right)={\frac {\operatorname {sl} \left({\sqrt[{4}]{-1}}z\right)}{\sqrt[{4}]{-1}}}}
This is analogous to the relationship between hyperbolic and trigonometric sine:
sinh
z
=
−
i
sin
(
i
z
)
=
sin
(
−
1
2
z
)
−
1
2
{\displaystyle \sinh z=-i\sin(iz)={\frac {\sin \left({\sqrt[{2}]{-1}}z\right)}{\sqrt[{2}]{-1}}}}
With respect to the quartic Fermat curve
x
4
+
y
4
=
1
{\displaystyle x^{4}+y^{4}=1}
, the hyperbolic lemniscate sine is analogous to the trigonometric tangent function.
In a quartic Fermat curve
x
4
+
y
4
=
1
{\displaystyle x^{4}+y^{4}=1}
squircle ) the hyperbolic lemniscate sine and cosine are analogous to the tangent and cotangent functions in a unit circle
x
2
+
y
2
=
1
{\displaystyle x^{2}+y^{2}=1}
L L
x
=
1
{\displaystyle x=1}
[46]
The hyperbolic lemniscate sine satisfies the argument addition identity:
slh
(
a
+
b
)
=
slh
a
1
+
slh
4
b
+
slh
b
1
+
slh
4
a
1
−
slh
2
a
slh
2
b
{\displaystyle \operatorname {slh} (a+b)={\frac {\operatorname {slh} a{\sqrt {1+\operatorname {slh} ^{4}b}}+\operatorname {slh} b{\sqrt {1+\operatorname {slh} ^{4}a}}}{1-\operatorname {slh} ^{2}a\,\operatorname {slh} ^{2}b}}}
The derivative can be expressed in this way:
d
d
x
slh
x
=
1
+
slh
4
x
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {slh} x={\sqrt {1+\operatorname {slh} ^{4}x}}}
Furthermore the function
sin
4
(
t
)
{\displaystyle \sin _{4}(t)}
cot
4
(
t
)
{\displaystyle \cot _{4}(t)}
tlh
(
t
)
=
sin
4
(
t
)
{\displaystyle {\text{tlh}}(t)=\sin _{4}(t)}
ctlh
(
t
)
=
cos
4
(
t
)
{\displaystyle {\text{ctlh}}(t)=\cos _{4}(t)}
Number theory [ ] In algebraic number theory , every abelian extension of the Gaussian rationals
Q
(
i
)
{\displaystyle \mathbf {Q} (i)}
sl
z
{\displaystyle \operatorname {sl} z}
z
{\displaystyle z}
sl
m
z
=
0
{\displaystyle \operatorname {sl} mz=0}
m
{\displaystyle m}
[47] Kronecker–Weber theorem for the rational numbers
Q
{\displaystyle \mathbf {Q} }
Hilbert's twelfth problem .
The field
Q
(
i
,
sl
(
ϖ
/
n
)
)
{\displaystyle \mathbf {Q} (i,\operatorname {sl} (\varpi /n))}
n
{\displaystyle n}
Q
(
i
)
{\displaystyle \mathbf {Q} (i)}
x
{\displaystyle x}
y
{\displaystyle y}
(
1
+
i
)
n
{\displaystyle (1+i)n}
torsion points on the elliptic curve
y
2
=
4
x
3
+
x
{\displaystyle y^{2}=4x^{3}+x}
[48]
World map projections [ ]
"The World on a Quincuncial Projection", from Peirce (1879).
The Peirce quincuncial projection , designed by Charles Sanders Peirce of the US Coast Survey in the 1870s, is a world map projection based on the inverse lemniscate sine of stereographically projected points (treated as complex numbers).[49]
When lines of constant real or imaginary part are projected onto the complex plane via the hyperbolic lemniscate sine, and thence stereographically projected onto the sphere (see Riemann sphere ), the resulting curves are spherical conics , the spherical analog of planar ellipses and hyperbolas .[50] Jacobi elliptic functions ) provide a parametrization for spherical conics.
A conformal map projection from the globe onto the 6 square faces of a cube can also be defined using the lemniscate functions.[51] partial differential equations can be effectively solved by conformal mapping, this map from sphere to cube is convenient for atmospheric modeling .[52]
See also [ ] External links [ ] Notes [ ]
^ Gauss used the symbols sl and cl for the lemniscate sine and cosine, respectively. Ayoub (1984) uses sinlem and coslem . Whittaker and Watson (1920) use the symbols sin lemn and cos lemn . Some sources use the generic letters s c φ φ′
^ The fundamental periods
(
1
+
i
)
ϖ
{\displaystyle (1+i)\varpi }
(
1
−
i
)
ϖ
{\displaystyle (1-i)\varpi }
^ Robinson (2019a) starts from this definition and thence derives other properties of the lemniscate functions.
^ This map was the first ever picture of a Schwarz–Christoffel mapping, in Schwarz (1869) p. 113 .
^ Euler (1761), Siegel (1969). Prasolov & Solovyev (1997) use the polar-coordinate representation of the Lemniscate to derive differential arc length, but the result is the same.
^ Siegel (1969), Schappacher (1997)
^ Such numbers are OEIS sequence A003401 .
^ Abel (1827–1828), Rosen (1981), Prasolov & Solovyev (1997)
^ Euler (1786), Sridharan (2004), Levien (2008)
^ Dark areas represent zeros, and bright areas represent poles. As the argument of
sl
z
{\displaystyle \operatorname {sl} z}
−
π
{\displaystyle -\pi }
−
π
{\displaystyle -\pi }
π
{\displaystyle \pi }
(
Arg
≈
−
π
/
2
)
{\displaystyle (\operatorname {Arg} \approx -\pi /2)}
(
Arg
≈
0
)
{\displaystyle (\operatorname {Arg} \approx 0)}
(
Arg
≈
π
/
2
)
{\displaystyle (\operatorname {Arg} \approx \pi /2)}
(
Arg
≈
π
)
{\displaystyle (\operatorname {Arg} \approx \pi )}
^ Schappacher (1997). OEIS sequence A062539 lists the lemniscate constant's decimal digits.
^ Schneider (1937)
^ G. V. Choodnovsky: Algebraic independence of constants connected with the functions of analysis , Notices of the AMS 22, 1975, p. A-486
^ G. V. Chudnovsky: Contributions to The Theory of Transcendental Numbers , American Mathematical Society, 1984, p. 6
^ Levien (2008). Todd (1975) calls these two factors
A
=
ϖ
/
2
{\displaystyle A=\varpi /2}
B
=
π
/
2
ϖ
{\displaystyle B=\pi /2\varpi }
^ Levin (2006)
^ Hyde (2014) proves the validity of a more general Wallis-like formula for clover curves; here the special case of the lemniscate is slightly transformed, for clarity.
^ Bottazzini & Gray (2013), p. 60
^ Todd (1975)
^ Eymard, Pierre; Lafon, Jean-Pierre (1999). Autour du nombre Pi (in French). HERMANN. ISBN 2705614435 ^ Combining the first and fourth identity gives
sl
z
=
−
i
/
sl
(
z
−
(
1
+
i
)
ϖ
/
2
)
{\displaystyle \operatorname {sl} z=-i/\operatorname {sl} (z-(1+i)\varpi /2)}
Autour du nombre Pi (p. 218) without the minus sign at the front of the right-hand side.
^ The even Gaussian integers are the residue class of 0, modulo 1 + i , the black squares on a checkerboard .
^ Prasolov & Solovyev (1997), Robinson (2019a)
^ Eymard, Pierre; Lafon, Jean-Pierre (1999). Autour du nombre Pi (in French). HERMANN. ISBN 2705614435 ^ Bottazzini, Umberto; Gray, Jeremy (2013). Hidden Harmony—Geometric Fantasies . Springer. ISBN 978-1-4614-5724-4 ^ Gauss expanded the products for
M
{\displaystyle M}
N
{\displaystyle N}
M
{\displaystyle M}
N
{\displaystyle N}
N
(
2
z
)
=
M
4
(
z
)
+
N
4
(
z
)
{\displaystyle N(2z)=M^{4}(z)+N^{4}(z)}
^ a b Reinhardt, W. P.; Walker, P. L. (2010), "Jacobian Elliptic Functions" , in Olver, Frank W. J. ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 MR 2723248 ^ Analogously,
1
sin
z
=
∑
n
∈
Z
(
−
1
)
n
z
−
n
π
.
{\displaystyle {\frac {1}{\sin z}}=\sum _{n\in \mathbb {Z} }{\frac {(-1)^{n}}{z-n\pi }}.}
^ Lindqvist & Peetre (2001) generalizes the first of these forms.
^ Ayoub (1984), Prasolov & Solovyev (1997)
^ Euler (1761), §44 p. 79 , §47 pp. 80–81
^ a b Euler (1761) §46 p. 80
^ Rosen (1981)
^ "A104203" . The On-Line Encyclopedia of Integer Sequences .^ Robinson (2019a)
^ Eymard, Pierre; Lafon, Jean-Pierre (1999). Autour du nombre Pi (in French). HERMANN. ISBN 2705614435 ^ The identity
cl
z
=
cn
(
2
z
;
1
2
)
{\displaystyle \operatorname {cl} z={\operatorname {cn} }\left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right)}
p. 33 .
^ Reinhardt & Walker (2010), §22.20(ii)
^ Carlson (2010), §19.8
^ Dieckmann, Andreas. "Collection of Infinite Products and Series" . ^ Vigren & Dieckmann (2020), p. 7
^ In general,
sinh
(
x
−
n
π
)
{\displaystyle \sinh(x-n\pi )}
sin
(
x
−
n
π
i
)
=
−
i
sinh
(
i
x
+
n
π
)
{\displaystyle \sin(x-n\pi i)=-i\sinh(ix+n\pi )}
^ Reinhardt & Walker (2010), 22.11
^ Reinhardt & Walker (2010), 22.2.E7
^ Berndt, Bruce C. (1994). Ramanujan's Notebooks Part IV (First ed.). Springer Science+Business Media New York. ISBN 978-1-4612-6932-8 ^ Levin (2006), Robinson (2019b)
^ Ogawa (2005)
^ Cox, David A. (2012). Galois Theory (Second ed.). Wiley. ISBN 978-1-118-07205-9 ^ Peirce (1879). Guyou (1887) and Adams (1925) introduced transverse and oblique aspects of the same projection, respectively. Also see Lee (1976). These authors write their projection formulas in terms of Jacobi elliptic functions, with a square lattice.
^ Adams (1925)
^ Adams (1925), Lee (1976).
^ Rančić, Purser, & Mesinger (1996); McGregor (2005).
References [ ]
Abel, Niels Henrik (1827–1828). "Recherches sur les fonctions elliptiques" [Research on elliptical functions]. Crelle's Journal (in French). 1827 (2): 101–181. doi :10.1515/crll.1827.2.101 ."Recherches sur les fonctions elliptiques" . Crelle's Journal . 1828 (3): 160–190. doi :10.1515/crll.1828.3.160 .Adams, Oscar Sherman (1925). Elliptic functions applied to conformal world maps (PDF) . US Government Printing Office. (1984). "The Lemniscate and Fagnano's Contributions to Elliptic Integrals". Archive for History of Exact Sciences . 29 (2): 131–149. JSTOR 41133708 . Bottazzini, Umberto ; Gray, Jeremy (2013). Hidden Harmony – Geometric Fantasies: The Rise of Complex Function Theory . Springer. doi :10.1007/978-1-4614-5725-1 . (2010), "Elliptic Integrals" , in Olver, Frank W. J. ; et al. (eds.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 MR 2723248 Cox, David Archibald (2012). "The Lemniscate". Galois Theory . Wiley. pp. 463–514. doi :10.1002/9781118218457.ch15 . ISBN 978-1-118-21845-7 Cox, David Archibald; Hyde, Trevor (2014). "The Galois theory of the lemniscate" (PDF) . Journal of Number Theory . 135 : 43–59. arXiv :1208.2653 doi :10.1016/j.jnt.2013.08.006 . Enneper, Alfred (1890) [1st ed. 1876]. "Note III: Historische Notizen über geometrische Anwendungen elliptischer Integrale." [Historical notes on geometric applications of elliptic integrals]. Elliptische Functionen, Theorie und Geschichte (in German). Nebert. pp. 524–547.Euler, Leonhard (1761). "Observationes de comparatione arcuum curvarum irrectificibilium" [Observations on the comparison of arcs of irrectifiable curves]. Novi Commentarii Academiae Scientiarum Imperialis Petropolitanae (in Latin). 6 : 58–84.E 252 . (Figures )Euler, Leonhard (1786). "De miris proprietatibus curvae elasticae sub aequatione
y
=
∫
x
x
d
x
/
1
−
x
4
{\textstyle y=\int xx\mathop {\mathrm {d} x} {\big /}{\sqrt {1-x^{4}}}}
[On the amazing properties of elastic curves contained in equation
y
=
∫
x
x
d
x
/
1
−
x
4
{\textstyle y=\int xx\mathop {\mathrm {d} x} {\big /}{\sqrt {1-x^{4}}}}
Acta Academiae Scientiarum Imperialis Petropolitanae (in Latin). 1782 (2): 34–61. 605 .Fagnano, Giulio Carlo (1718–1723). "Metodo per misurare la lemniscata" [Method for measuring the lemniscate]. Giornale de' letterati d'Italia (in Italian). 29 : 258–269."Giunte al primo schediasma sopra la Lemniscata" . Giornale de' letterati d'Italia . 34 : 197–207."Metodo per misurare la lemniscata, schediasma II" . Giornale de' letterati d'Italia . 30 : 87–111.Fagnano (1911) [1850]. Opere Matematiche, vol. 2 Figures )Greenhill, Alfred George (1892). The Applications of Elliptic Functions Guyou, Émile (1887). "Nouveau système de projection de la sphère: Généralisation de la projection de Mercator" [New system of projection of the sphere]. Annales Hydrographiques, Ser. 2 (in French). 9 : 16–35. (1978). "Fonctions elliptiques et intégrales abéliennes" [Elliptic functions and Abelian integrals]. In Dieudonné, Jean (ed.). Abrégé d'histoire des mathématiques, 1700–1900. II (in French). Hermann. pp. 1–113. Hyde, Trevor (2014). "A Wallis product on clovers" (PDF) . The American Mathematical Monthly . 121 (3): 237–243. doi :10.4169/amer.math.monthly.121.03.237 . Kubota, Tomio (1964). "Some arithmetical applications of an elliptic function". Crelle's Journal . 1964 (214/215): 141–145. doi :10.1515/crll.1964.214-215.141 .Langer, Joel C.; Singer, David A. (2010). "Reflections on the Lemniscate of Bernoulli: The Forty-Eight Faces of a Mathematical Gem" (PDF) . Milan Journal of Mathematics . 78 (2): 643–682. doi :10.1007/s00032-010-0124-5 . Langer, Joel C.; Singer, David A. (2011). "The lemniscatic chessboard" . Forum Geometricorum . 11 : 183–199. Lawden, Derek Frank (1989). Elliptic Functions and Applications . Springer-Verlag. doi :10.1007/978-1-4757-3980-0 .Lee, Laurence Patrick (1976). Conformal Projections Based on Elliptic Functions Cartographica Monograph. 16 . University of Toronto Press. Levien, Raph (2008). The elastica: a mathematical history (PDF) (Technical report). University of California at Berkeley. UCB/EECS-2008-103.Levin, Aaron (2006). "A Geometric Interpretation of an Infinite Product for the Lemniscate Constant". The American Mathematical Monthly . 113 (6): 510–520. JSTOR 27641976 . Lindqvist, Peter; Peetre, Jaak (2001). "Two Remarkable Identities, Called Twos, for Inverses to Some Abelian Integrals" (PDF) . The American Mathematical Monthly . 108 (5): 403–410. JSTOR 2695794 . Markushevich, Aleksei Ivanovich (1966). The Remarkable Sine Functions Markushevich, Aleksei Ivanovich (1992). Introduction to the Classical Theory of Abelian Functions . American Mathematical Society. doi :10.1090/mmono/096 . McGregor, John L. (2005). C-CAM: Geometric Aspects and Dynamical Formulation CSIRO Atmospheric Research . 70. McKean, Henry ; Moll, Victor (1999). Elliptic Curves: Function Theory, Geometry, Arithmetic . Cambridge. ISBN 9780521582285 Milne-Thomson, Louis Melville (1964). "16. Jacobian Elliptic Functions and Theta Functions" . In Abramowitz, Milton ; Stegun, Irene Ann (eds.). Handbook of Mathematical Functions Neuman, Edward (2007). "On Gauss lemniscate functions and lemniscatic mean" (PDF) . Mathematica Pannonica . 18 (1): 77–94.Nishimura, Ryo (2015). "New properties of the lemniscate function and its transformation" . Journal of Mathematical Analysis and Applications . 427 (1): 460–468. Ogawa, Takuma (2005). "Similarities between the trigonometric function and the lemniscate function from arithmetic view point" . Tsukuba Journal of Mathematics . 29 (1). Peirce, Charles Sanders (1879). "A Quincuncial Projection of the Sphere" . American Journal of Mathematics . 2 (4): 394–397.Popescu-Pampu, Patrick (2016). What is the Genus? . Springer. doi :10.1007/978-3-319-42312-8 . Prasolov, Viktor; Solovyev, Yuri (1997). "4. Abel's Theorem on Division of Lemniscate". Elliptic functions and elliptic integrals . American Mathematical Society. doi :10.1090/mmono/170 . Rančić, Miodrag; Purser, R. James; Mesinger, Fedor (1996). "A global shallow-water model using an expanded spherical cube: Gnomonic versus conformal coordinates". Quarterly Journal of the Royal Meteorological Society . 122 (532): 959–982. doi :10.1002/qj.49712253209 . Reinhardt, William P.; Walker, Peter L. (2010), "22. Jacobian Elliptic Functions" , in Olver, Frank W. J. ; et al. (eds.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 MR 2723248 Reinhardt, William P.; Walker, Peter L. (2010), "23. Weierstrass Elliptic and Modular Functions" , in Olver, Frank W. J. ; et al. (eds.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 MR 2723248 Robinson, Paul L. (2019a). "The Lemniscatic Functions". arXiv :1902.08614 Robinson, Paul L. (2019b). "The Elliptic Functions in a First-Order System". arXiv :1903.07147 Rosen, Michael (1981). "Abel's Theorem on the Lemniscate". The American Mathematical Monthly . 88 (6): 387–395. JSTOR 2321821 .Schappacher, Norbert (1997). "Some milestones of lemniscatomy" (PDF) . In Sertöz, S. (ed.). Algebraic Geometry (Proceedings of Bilkent Summer School, August 7–19, 1995, Ankara, Turkey). Marcel Dekker. pp. 257–290.Schneider, Theodor (1937). "Arithmetische Untersuchungen elliptischer Integrale" [Arithmetic investigations of elliptic integrals]. Mathematische Annalen (in German). 113 (1): 1–13. doi :10.1007/BF01571618 .Schwarz, Hermann Amandus (1869). "Ueber einige Abbildungsaufgaben" [About some mapping problems]. Crelle's Journal (in German). 70 : 105–120. doi :10.1515/crll.1869.70.105 .Siegel, Carl Ludwig (1969). "1. Elliptic Functions". Topics in Complex Function Theory, Vol. I . Wiley-Interscience. pp. 1–89. ISBN 0-471-60844-0 MR 0257326 .Snape, Jamie (2004). "Bernoulli's Lemniscate". Applications of Elliptic Functions in Classical and Algebraic Geometry Southard, Thomas H. (1964). "18. Weierstrass Elliptic and Related Functions" . In Abramowitz, Milton ; Stegun, Irene Ann (eds.). Handbook of Mathematical Functions Sridharan, Ramaiyengar (2004). "Physics to mathematics: from lintearia to lemniscate – I" (PDF) . Resonance . 9 (4): 21–29."From lintearia to lemniscate II: Gauss and Landen's Work" (PDF) . Resonance . 9 (6): 11–20.Todd, John (1975). "The lemniscate constants". Communications of the ACM . 18 (1): 14–19. doi :10.1145/360569.360580 .Vigren, Erik; Dieckmann, Andreas (21 June 2020). "Simple Solutions of Lattice Sums for Electric Fields Due to Infinitely Many Parallel Line Charges" . Symmetry . 12 (6): 1040. Whittaker, Edmund Taylor ; Watson, George Neville (1920) [1st ed. 1902]. "22.8 The lemniscate functions" . A Course of Modern Analysis





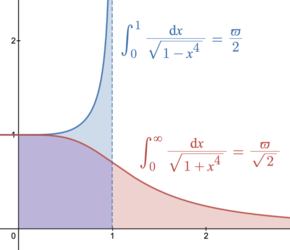


























![{\displaystyle r\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d4a8acea9f5c4e59d8f5fd0ea3c695efa7252fe)

![{\displaystyle {\begin{aligned}&\int _{0}^{r}{\sqrt {x'(t)^{2}+y'(t)^{2}}}\mathop {\mathrm {d} t} \\&\quad {}=\int _{0}^{r}{\sqrt {{\frac {(1+2t^{2})^{2}}{2(1+t^{2})}}+{\frac {(1-2t^{2})^{2}}{2(1-t^{2})}}}}\mathop {\mathrm {d} t} \\[6mu]&\quad {}=\int _{0}^{r}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}\\[6mu]&\quad {}=\operatorname {arcsl} r.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49646481c38b1e3eb1ab582491a98c24fb78c899)

![{\displaystyle {\begin{aligned}&\int _{r}^{1}{\sqrt {x'(t)^{2}+y'(t)^{2}}}\mathop {\mathrm {d} t} \\&\quad {}=\int _{r}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}\\[6mu]&\quad {}=\operatorname {arccl} r={\tfrac {1}{2}}\varpi -\operatorname {arcsl} r.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/951483e802c58ce9f682e50c2662b425002a37aa)









![{\displaystyle {\begin{aligned}\varpi &=2\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}={\sqrt {2}}\int _{0}^{\infty }{\frac {\mathrm {d} t}{\sqrt {1+t^{4}}}}=\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {t-t^{3}}}}\\[6mu]&=4\int _{0}^{\infty }{\Bigl (}{\sqrt[{4}]{1+t^{4}}}-t{\Bigr )}\,\mathrm {d} t=2{\sqrt {2}}\int _{0}^{1}{\sqrt[{4}]{1-t^{4}}}\mathop {\mathrm {d} t} =3\int _{0}^{1}{\sqrt {1-t^{4}}}\,\mathrm {d} t\\[2mu]&={\tfrac {1}{2}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )}={\frac {\Gamma {\bigl (}{\tfrac {1}{4}}{\bigr )}^{2}}{2{\sqrt {2\pi }}}}={\frac {\pi }{{\operatorname {M} }{\bigl (}1,{\sqrt {2}}{\bigr )}}}={\sqrt {\pi }}e^{\beta '(0)}\\[5mu]&=2.62205\;75542\;92119\;81046\;48395\;89891\;11941\ldots ,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3cd0d4c6827a40c6e093ae29bbb2d7a18ac4c6a)






![{\textstyle 2\int _{0}^{1}{\sqrt[{n}]{1-x^{n}}}\mathop {\mathrm {d} x} ={\tfrac {1}{n}}\pi _{n}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba1088ee33b310fd26307c26b917b43a7a9211ae)















![{\displaystyle \sum _{z\in \mathbf {Z} [i]\setminus \{0\}}{\frac {1}{z^{4}}}=G_{4}(i)={\frac {\varpi ^{4}}{15}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ca287a815279223c71f1c9ee37ca50d74da29be)
![\mathbf {Z} [i]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0a617cf5867f951fefb72f3ab7278e0f6f1eedd)




![{\displaystyle {\begin{aligned}{\operatorname {cl} }{\bigl (}z\pm {\tfrac {1}{2}}\varpi {\bigr )}&=\mp \operatorname {sl} z,&{\operatorname {cl} }{\bigl (}z\pm {\tfrac {1}{2}}i\varpi {\bigr )}&={\frac {\mp i}{\operatorname {sl} z}}\\[6mu]{\operatorname {sl} }{\bigl (}z\pm {\tfrac {1}{2}}\varpi {\bigr )}&=\pm \operatorname {cl} z,&{\operatorname {sl} }{\bigl (}z\pm {\tfrac {1}{2}}i\varpi {\bigr )}&={\frac {\pm i}{\operatorname {cl} z}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3960242e95aeb8d86d7c6666d4887c160fbac91c)



![{\displaystyle {\begin{aligned}\operatorname {cl} (z+\varpi )&=\operatorname {cl} (z+i\varpi )=-\operatorname {cl} z\\[4mu]\operatorname {sl} (z+\varpi )&=\operatorname {sl} (z+i\varpi )=-\operatorname {sl} z\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee4add8875fadf39f2e07fd34c565655b2e2b236)


![{\displaystyle {\begin{aligned}{\operatorname {cl} }{\bigl (}z+(1+i)\varpi {\bigr )}&={\operatorname {cl} }{\bigl (}z+(1-i)\varpi {\bigr )}=\operatorname {cl} z\\[4mu]{\operatorname {sl} }{\bigl (}z+(1+i)\varpi {\bigr )}&={\operatorname {sl} }{\bigl (}z+(1-i)\varpi {\bigr )}=\operatorname {sl} z\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1d7545373f396158c72d1b376d96364cedff009)
![{\displaystyle {\begin{aligned}\operatorname {cl} {\bar {z}}&={\overline {\operatorname {cl} z}}\\[6mu]\operatorname {sl} {\bar {z}}&={\overline {\operatorname {sl} z}}\\[4mu]\operatorname {cl} iz&={\frac {1}{\operatorname {cl} z}}\\[6mu]\operatorname {sl} iz&=i\operatorname {sl} z\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cee565bde6b2129ca509f1e6fe214975ad634ae)






















![{\displaystyle {\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {cl} z=\operatorname {cl'} z&=-\operatorname {sl} z\,{\bigl (}1+\operatorname {cl^{2}} z{\bigr )}\\\operatorname {cl'^{2}} z&=1-\operatorname {cl^{4}} z\\[5mu]{\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {sl} z=\operatorname {sl'} z&=\operatorname {cl} z\,{\bigl (}1+\operatorname {sl^{2}} z{\bigr )}\\\operatorname {sl'^{2}} z&=1-\operatorname {sl^{4}} z\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f4c6a7e2511c4078b756f21a0e451b8a64ee1bf)







![{\displaystyle {\begin{aligned}\operatorname {cl} (u+v)&=\operatorname {cl} u\,\operatorname {cl} v\ominus \operatorname {sl} u\,\operatorname {sl} v={\frac {\operatorname {cl} u\,\operatorname {cl} v-\operatorname {sl} u\,\operatorname {sl} v}{1+\operatorname {sl} u\,\operatorname {cl} u\,\operatorname {sl} v\,\operatorname {cl} v}}\\[2mu]\operatorname {cl} (u-v)&=\operatorname {cl} u\,\operatorname {cl} v\oplus \operatorname {sl} u\,\operatorname {sl} v\\[2mu]\operatorname {sl} (u+v)&=\operatorname {sl} u\,\operatorname {cl} v\oplus \operatorname {cl} u\,\operatorname {sl} v={\frac {\operatorname {sl} u\,\operatorname {cl} v+\operatorname {cl} u\,\operatorname {sl} v}{1-\operatorname {sl} u\,\operatorname {cl} u\,\operatorname {sl} v\,\operatorname {cl} v}}\\[2mu]\operatorname {sl} (u-v)&=\operatorname {sl} u\,\operatorname {cl} v\ominus \operatorname {cl} u\,\operatorname {sl} v\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b30e48fbafa5e12f8a952c1f0b8e279f0f9cf5fc)
![{\displaystyle {\begin{aligned}\cos(u\pm v)&=\cos u\,\cos v\mp \sin u\,\sin v\\[6mu]\sin(u\pm v)&=\sin u\,\cos v\pm \cos u\,\sin v\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89f19808c18b020503e6fc6074aa10141883d798)

















![{\displaystyle {\tfrac {1}{2}}({\sqrt[{4}]{5}}-1)\left({\sqrt {{\sqrt {5}}+2}}-1\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78842c8c6060cec842d54b0d525503c394649a75)
![{\displaystyle {\tfrac {1}{2{\sqrt[{4}]{2}}}}({\sqrt {5}}-1){\sqrt {{\sqrt[{4}]{20}}+{\sqrt {{\sqrt {5}}-1}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1eb58c50fee1e991176bb324599b4d43947c6c28)

![{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt {3}}+1-{\sqrt[{4}]{12}}{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c74fc1a430f5e7bb0244a281a1d4f1d0647ca67)
![{\displaystyle {\sqrt[{4}]{2{\sqrt {3}}-3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32e7446bf7046ae049852dbd22d5dc78e374b060)



![{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt[{4}]{5}}-1{\bigr )}{\Bigl (}{\sqrt {{\sqrt {5}}+2}}+1{\Bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7aa6255bad54d95861f1c91c7dae1110c139d67f)
![{\displaystyle {\tfrac {1}{\sqrt {2}}}{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {{\sqrt {2{\bigl (}5-{\sqrt {5}}{\bigr )}}}+1-{\sqrt {5}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2f758a0ba20b6e2b74b2b639c48d58573c86bb7)


![{\displaystyle {\sqrt {{\bigl (}{\sqrt[{4}]{2}}-1{\bigr )}{\Bigl (}{\sqrt {2}}+1+{\sqrt {2+{\sqrt {2}}}}{\Bigr )}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69e0a7a05939422e6aadd7a3aa97292b6c764ccc)
![{\displaystyle {\sqrt {{\bigl (}{\sqrt[{4}]{2}}-1{\bigr )}{\Bigl (}{\sqrt {2}}+1-{\sqrt {2+{\sqrt {2}}}}{\Bigr )}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d116792170cb8e87e734f4ede9d92de41a374c5c)

![{\displaystyle {\tfrac {1}{\sqrt {2}}}{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {{\sqrt {2{\bigl (}5-{\sqrt {5}}{\bigr )}}}-1+{\sqrt {5}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ee79a058fcbe0a7ca46be4da520abb70225a15f)
![{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt[{4}]{5}}-1{\bigr )}{\Bigl (}{\sqrt {{\sqrt {5}}+2}}-1{\Bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99990d06fac9e81d0fe3fc2d3f75ff0ebd59f28d)




























![{\displaystyle \prod _{k=1}^{n}\;{\operatorname {sl} }{\left({\frac {2k-1}{2n+1}}{\frac {\varpi }{2}}\right)}={\sqrt[{8}]{\frac {\lambda ((2n+1)i)}{1-\lambda ((2n+1)i)}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3cb5d4df31aa6a387b048c66646e6f722f3b5f4)
![{\displaystyle {\begin{aligned}&{\operatorname {sl} }{\bigl (}{\tfrac {1}{14}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {3}{14}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {5}{14}}\varpi {\bigr )}\\[7mu]&\quad {}={\sqrt[{8}]{\frac {\lambda (7i)}{1-\lambda (7i)}}}={\tan }{\Bigl (}{{\tfrac {1}{2}}\operatorname {arccsc} }{\Bigl (}{\tfrac {1}{2}}{\sqrt {8{\sqrt {7}}+21}}+{\tfrac {1}{2}}{\sqrt {7}}+1{\Bigr )}{\Bigr )}\\[18mu]&{\operatorname {sl} }{\bigl (}{\tfrac {1}{18}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {3}{18}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {5}{18}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {7}{18}}\varpi {\bigr )}\\[-3mu]&\quad {}={\sqrt[{8}]{\frac {\lambda (9i)}{1-\lambda (9i)}}}={\tan }{\Biggl (}{\frac {\pi }{4}}-{\arctan }{\Biggl (}{\frac {2{\sqrt[{3}]{2{\sqrt {3}}-2}}-2{\sqrt[{3}]{2-{\sqrt {3}}}}+{\sqrt {3}}-1}{\sqrt[{4}]{12}}}{\Biggr )}{\Biggr )}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a37cc09da1938f7505b12780af4a9d2073a6e404)




















![{\displaystyle {\text{sl}}{\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=f{\biggl (}{\frac {4\pi }{\varpi }}\sin(x)\sum _{n=1}^{\infty }{\frac {\cosh[(2n-1)\pi ]}{\cosh[(2n-1)\pi ]^{2}-\cos(x)^{2}}}{\biggr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/180ffc565dfe165b60463bad1384f810f23f3f43)
![{\displaystyle {\text{cl}}{\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=f{\biggl (}{\frac {4\pi }{\varpi }}\cos(x)\sum _{n=1}^{\infty }{\frac {\cosh[(2n-1)\pi ]}{\cosh[(2n-1)\pi ]^{2}-\sin(x)^{2}}}{\biggr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/682cfa655a0ef3914503e11fdfdcd563e7fe69ef)
![{\displaystyle \mathrm {sl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=2\exp {\bigl (}{-{\tfrac {1}{4}}\pi }{\bigr )}\sin(x)\prod _{n=1}^{\infty }{\frac {1-2\cos(2x)\exp(-2n\pi )+\exp(-4n\pi )}{1+2\cos(2x)\exp[-(2n-1)\pi ]+\exp[-(4n-2)\pi ]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd5c3cb7c2623c032e244961851a9e5f3f4e6a65)
![{\displaystyle \mathrm {cl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=2\exp {\bigl (}{-{\tfrac {1}{4}}\pi }{\bigr )}\cos(x)\prod _{n=1}^{\infty }{\frac {1+2\cos(2x)\exp(-2n\pi )+\exp(-4n\pi )}{1-2\cos(2x)\exp[-(2n-1)\pi ]+\exp[-(4n-2)\pi ]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e1dc1bcc89672f80fa07de50e82916cf4e294ee)









![{\displaystyle \operatorname {arcsl} x={\frac {1}{\sqrt {2}}}F\left[{\arcsin }{\left({\frac {{\sqrt {2}}x}{\sqrt {1+x^{2}}}}\right)};{\frac {1}{\sqrt {2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce6d3c6da18998637695882e5bdd8f18488239e2)
![{\displaystyle \operatorname {arcsl} x=2({\sqrt {2}}-1)F\left[{\arcsin }{\left[{\frac {({\sqrt {2}}+1)x}{{\sqrt {1+x^{2}}}+1}}\right]};({\sqrt {2}}-1)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/082f9ac2a6d313bcb0f777178637ccc5ad369d4f)
![{\displaystyle {\begin{aligned}\operatorname {arcsl} x={}&{\frac {2+{\sqrt {2}}}{2}}E\left[{\arcsin }{\left[{\frac {({\sqrt {2}}+1)x}{{\sqrt {1+x^{2}}}+1}}\right]};({\sqrt {2}}-1)^{2}\right]\\[5mu]&\ \ -E\left[{\arcsin }{\left({\frac {{\sqrt {2}}x}{\sqrt {1+x^{2}}}}\right)};{\frac {1}{\sqrt {2}}}\right]+{\frac {x{\sqrt {1-x^{2}}}}{{\sqrt {2}}(1+x^{2}+{\sqrt {1+x^{2}}})}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26266eedc703b0a51abcef58e19b9575b5be6ff5)
![{\displaystyle \operatorname {arccl} x={\frac {1}{\sqrt {2}}}F\left[\arccos x;{\frac {1}{\sqrt {2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b65947bd14c78f1a6bac165d3863e40dfd1d5ed1)




![{\displaystyle \int {\frac {1}{\sqrt[{4}]{(1-x^{4})^{3}}}}\,\mathrm {d} x={{\sqrt {2}}\operatorname {arcsl} }{\left({\frac {x}{\sqrt {1+{\sqrt {1-x^{4}}}}}}\right)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2de4beeffaad963da9c01cdf7b35d1f0af381775)
![{\displaystyle \int {\frac {1}{\sqrt[{4}]{(x^{4}+1)^{3}}}}\,\mathrm {d} x={\operatorname {arcsl} }{\left({\frac {x}{\sqrt[{4}]{x^{4}+1}}}\right)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b5752ada1cfac9f4070b4f8eb7d332bf2b1cffe)
![{\displaystyle \int {\frac {1}{\sqrt[{4}]{(1-x^{2})^{3}}}}\,\mathrm {d} x={2\operatorname {arcsl} }{\left({\frac {x}{1+{\sqrt {1-x^{2}}}}}\right)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0252742192c63ec60f1002a1865a36afd513becf)
![{\displaystyle \int {\frac {1}{\sqrt[{4}]{(x^{2}+1)^{3}}}}\,\mathrm {d} x={2\operatorname {arcsl} }{\left({\frac {x}{{\sqrt {x^{2}+1}}+1}}\right)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a44dd509f54c2df2294f27783ae519cd6791518a)
![{\displaystyle \int {\frac {1}{\sqrt[{4}]{(ax^{2}+bx+c)^{3}}}}\,\mathrm {d} x={{\frac {2{\sqrt {2}}}{\sqrt[{4}]{4a^{2}c-ab^{2}}}}\operatorname {arcsl} }{\left({\frac {2ax+b}{{\sqrt {4a(ax^{2}+bx+c)}}+{\sqrt {4ac-b^{2}}}}}\right)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be99ad74d6fec38e340ef4c87bc5da823a7876b3)










![{\displaystyle \operatorname {slh} z={\frac {1-i}{\sqrt {2}}}\operatorname {sl} \left({\frac {1+i}{\sqrt {2}}}z\right)={\frac {\operatorname {sl} \left({\sqrt[{4}]{-1}}z\right)}{\sqrt[{4}]{-1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56dd44181c73fe6b48af847f7fb236e52b7816a2)
![{\displaystyle \sinh z=-i\sin(iz)={\frac {\sin \left({\sqrt[{2}]{-1}}z\right)}{\sqrt[{2}]{-1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc66d9221d4e85075dc6e4e7eda93fb76745fb63)

































