15 puzzle

To solve the puzzle, the numbers must be rearranged into order

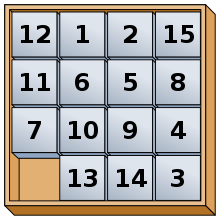
The 15 puzzle (also called Gem Puzzle, Boss Puzzle, Game of Fifteen, Mystic Square and many others) is a sliding puzzle having 15 square tiles numbered 1–15 in a frame that is 4 tiles high and 4 tiles wide, leaving one unoccupied tile position. Tiles in the same row or column of the open position can be moved by sliding them horizontally or vertically, respectively. The goal of the puzzle is to place the tiles in numerical order.

Named for the number of tiles in the frame, the 15 puzzle may also be called a 16 puzzle, alluding to its total tile capacity. Similar names are used for different sized variants of the 15 puzzle, such as the 8 puzzle that has 8 tiles in a 3×3 frame.

The n puzzle is a classical problem for modelling algorithms involving heuristics. Commonly used heuristics for this problem include counting the number of misplaced tiles and finding the sum of the taxicab distances between each block and its position in the goal configuration.^[1] Note that both are admissible, i.e. they never overestimate the number of moves left, which ensures optimality for certain search algorithms such as A*.^[1]

Mathematics[]

Solvability[]

A solved 15 puzzle

Johnson & Story (1879) used a parity argument to show that half of the starting positions for the n puzzle are impossible to resolve, no matter how many moves are made. This is done by considering a function of the tile configuration that is invariant under any valid move, and then using this to partition the space of all possible labeled states into two equivalence classes of reachable and unreachable states.

The invariant is the parity of the permutation of all 16 squares plus the parity of the taxicab distance (number of rows plus number of columns) of the empty square from the lower right corner. This is an invariant because each move changes both the parity of the permutation and the parity of the taxicab distance. In particular, if the empty square is in the lower right corner then the puzzle is solvable if and only if the permutation of the remaining pieces is even.

Johnson & Story (1879) also showed that the converse holds on boards of size m×n provided m and n are both at least 2: all even permutations are solvable. This is straightforward but a little messy to prove by induction on m and n starting with m=n=2. Archer (1999) gave another proof, based on defining equivalence classes via a hamiltonian path.

Wilson (1974) studied the generalization of the 15 puzzle to arbitrary finite graphs, the original problem being the case of a 4×4 grid graph. The problem has some degenerate cases where the answer is either trivial or a simple combination of the answers to the same problem on some subgraphs. Namely, for paths and polygons, the puzzle has no freedom; if the graph is disconnected, only the connected component of the vertex with the "empty space" is relevant; and if there is an articulation vertex the problem reduces to the same puzzle on each of the biconnected components of that vertex. Excluding these cases, Wilson showed that other than one exceptional graph on 7 vertices, it is possible to obtain all permutations unless the graph is bipartite, in which case exactly the even permutations can be obtained. The exceptional graph is a regular hexagon with one diagonal and a vertex at the center added; only 1/6 of its permutations can be attained.

For larger versions of the n puzzle, finding a solution is easy, but the problem of finding the shortest solution is NP-hard. It is also NP-hard to approximate the fewest slides within an additive constant, but there is a polynomial-time constant-factor approximation.^[2][3] For the 15 puzzle, lengths of optimal solutions range from 0 to 80 single-tile moves (there are 17 configurations requiring 80 moves)^[4][5] or 43 multi-tile moves;^[6] the 8 puzzle always can be solved in no more than 31 single-tile moves or 24 multi-tile moves (integer sequence A087725). The multi-tile metric counts subsequent moves of the empty tile in the same direction as one.^[6]

The number of possible positions of the 24 puzzle is 25!/2 ≈ 7.76×10²⁴ which is too many to calculate God's number. In 2011, lower bounds of 152 single-tile moves or 41 multi-tile moves had been established, as well as upper bounds of 208 single-tile moves or 109 multi-tile moves.^{[7][8][9][10]} In 2016, the upper bound was improved to 205 single-tile moves.^[11]

The transformations of the fifteen puzzle form a groupoid (not a group, as not all moves can be composed);^[12][13][14] this groupoid acts on configurations.

Group theory[]

Because the combinations of the 15 puzzle can be generated by 3-cycles, it can be proved that the 15 puzzle can be represented by the alternating group ${\displaystyle A_{15}}$.^[15] In fact, any ${\displaystyle 2k-1}$ sliding puzzle with square tiles of equal size can be represented by ${\displaystyle A_{2k-1}}$.

Alternate proof[]

This section does not cite any sources. Please help by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources:  –  ·  ·  · scholar · JSTOR (April 2021) (Learn how and when to remove this template message)

This section's tone or style may not reflect the encyclopedic tone used on Wikipedia. See Wikipedia's guide to writing better articles for suggestions. (April 2021) (Learn how and when to remove this template message)

In an alternate view of the problem, we can consider the invariant to be the sum of the parity of the number of inversions in the current order of the 15 numbered pieces and the parity of the difference in the row number of the empty square from the row number of the last row. (Let's call it row distance from the last row.) This is an invariant because each column move, when we move a piece within the same column, changes both the parity of the number of inversions (by changing the number of inversions by ±1, ±3) and the parity of the row distance from the last row (changing row distance by ±1); and each row move, when we move a piece within the same row, does not change any of the two parities. Now if we look at the solved state of the puzzle, this sum is even. Hence it is easy to prove by induction that any state of the puzzle for which the above sum is odd cannot be solvable. In particular, if the empty square is in the lower right corner (even anywhere in the last row) then the puzzle is solvable if and only if the number of inversions of the numbered pieces is even.

History[]

Sam Loyd's unsolvable 15 puzzle, with tiles 14 and 15 exchanged. This puzzle is not solvable as it would require a change of the invariant to move it to the solved state.

U.S. Political cartoon about finding a Republican presidential candidate in 1880

The puzzle was "invented" by Noyes Palmer Chapman,^[16] a postmaster in Canastota, New York, who is said to have shown friends, as early as 1874, a precursor puzzle consisting of 16 numbered blocks that were to be put together in rows of four, each summing to 34. Copies of the improved Fifteen Puzzle made their way to Syracuse, New York, by way of Noyes' son, Frank, and from there, via sundry connections, to Watch Hill, Rhode Island, and finally to Hartford (Connecticut), where students in the American School for the Deaf started manufacturing the puzzle and, by December 1879, selling them both locally and in Boston, Massachusetts. Shown one of these, Matthias Rice, who ran a fancy woodworking business in Boston, started manufacturing the puzzle sometime in December 1879 and convinced a "Yankee Notions" fancy goods dealer to sell them under the name of "Gem Puzzle". In late January 1880, Dr. Charles Pevey, a dentist in Worcester, Massachusetts, garnered some attention by offering a cash reward for a solution to the Fifteen Puzzle.^[16]

The game became a craze in the U.S. in 1880.^[17]

Noyes Chapman had applied for a patent on his "Block Solitaire Puzzle" on February 21, 1880. However, that patent was rejected, likely because it was not sufficiently different from the August 20, 1878 "Puzzle-Blocks" patent (US 207124) granted to Ernest U. Kinsey.^[16]

Sam Loyd[]

Sam Loyd's 1914 illustration of the unsolvable variation

Sam Loyd claimed from 1891 until his death in 1911 that he had invented the puzzle, for example writing in the Cyclopedia of Puzzles (published 1914): "The older inhabitants of Puzzleland will remember how in the early seventies I drove the entire world crazy over a little box of movable pieces which became known as the '14-15 Puzzle'."^{[18][failed verification]} However, Loyd had nothing to do with the invention or initial popularity of the puzzle, and in any case, the craze was in 1880, not the early 1870s. Loyd's first article about the puzzle was published in 1886, and it was not until 1891 that he first claimed to be the inventor.^[16][19]

Some later interest was fuelled by Loyd's offer of a $1,000 prize to anyone who could provide a solution for achieving a particular combination specified by Loyd, namely reversing the 14 and 15, which Loyd called the 14-15 puzzle.^[1] This is impossible, as had been shown over a decade earlier by Johnson & Story (1879), because it requires a transformation from an even to an odd permutation.

Miscellaneous[]

The Minus Cube, manufactured in the USSR, is a 3D puzzle with similar operations to the 15 puzzle.

Bobby Fischer was an expert at solving the 15-Puzzle.^[20] He had been timed to be able to solve it within 25 seconds; Fischer demonstrated this on November 8, 1972, on The Tonight Show Starring Johnny Carson.^[21][22]

See also[]

• Combination puzzles
• Jeu de taquin, an operation on skew Young tableaux similar to the moves of the 15 puzzle
• Klotski
• Mechanical puzzles
• Pebble motion problems
• Rubik's Cube
• Three cups problem

Notes[]

References[]

External links[]

Wikimedia Commons has media related to 15 puzzle.

• The history of the 15 puzzle
• Fifteen Puzzle Solution
• Maximal number of moves required for the m X n generalization of the 15 puzzle
• 15-Puzzle Optimal Solver with download (from Herbert Kociemba)