19 equal temperament

Figure 1: 19 TET on the syntonic temperament's tuning continuum at P5= 694.737 cents, from (Milne et al. 2007).^[1]

In music, 19 equal temperament, called 19 TET, 19 EDO ("Equal Division of the Octave"), or 19 ET, is the tempered scale derived by dividing the octave into 19 equal steps (equal frequency ratios). Each step represents a frequency ratio of ¹⁹√2, or 63.16 cents (Play (help·info)).

19 equal temperament keyboard, after Woolhouse (1835).^[2]

The fact that traditional western music maps unambiguously onto this scale (unless it presupposes 12-EDO enharmonic equivalences) makes it easier to perform such music in this tuning than in many other tunings.

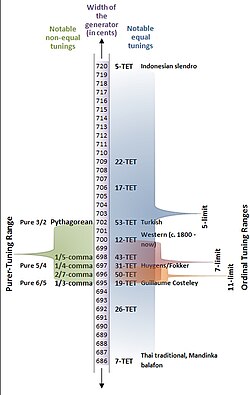
19 EDO is the tuning of the syntonic temperament in which the tempered perfect fifth is equal to 694.737 cents, as shown in Figure 1 (look for the label "19 TET"). On an isomorphic keyboard, the fingering of music composed in 19 EDO is precisely the same as it is in any other syntonic tuning (such as 12 EDO), so long as the notes are "spelled properly" — that is, with no assumption that the sharp below matches the flat immediately above it (enharmonicity).

Joseph Yasser's 19 equal temperament keyboard layout^[3]

The comparison between a standard 12 tone classical guitar and a 19 tone guitar design. This is the preliminary data that Arto Juhani Heino used to develop the "Artone 19" guitar design. The measurements are in millimeters.^[4]

History and use[]

Division of the octave into 19 equal-width steps arose naturally out of Renaissance music theory. The ratio of four minor thirds to an octave (648:625 or 62.565 cents – the "greater diesis") was almost exactly a nineteenth of an octave. Interest in such a tuning system goes back to the 16th century, when composer Guillaume Costeley used it in his chanson Seigneur Dieu ta pitié of 1558. Costeley understood and desired the circulating aspect of this tuning.

In 1577, music theorist Francisco de Salinas in effect proposed it. Salinas discussed 1⁄3 comma meantone, in which the fifth is of size 694.786 cents. The fifth of 19 EDO is 694.737 cents, which is less than a twentieth of a cent narrower: imperceptible and less than tuning error. Salinas suggested tuning nineteen tones to the octave to this tuning, which fails to close by less than a cent, so that his suggestion is effectively 19 EDO.

In the 19th century, mathematician and music theorist Wesley Woolhouse proposed it as a more practical alternative to meantone temperaments he regarded as better, such as 50 EDO.^[2]

The composer Joel Mandelbaum wrote his Ph.D. thesis^[5] on the properties of the 19 EDO tuning, and advocated for its use. In his thesis, he argued that it is the only viable system with a number of divisions between 12 and 22, and furthermore that the next smallest number of divisions resulting in a significant improvement in approximating just intervals is the 31 tone equal temperament.^[6] Mandelbaum and Joseph Yasser have written music with 19 EDO.^[7] Easley Blackwood has stated that 19 EDO makes possible "a substantial enrichment of the tonal repertoire".^[8]

Notation[]

Usual notation, as by Easley Blackwood^[9] and Wesley Woolhouse,^[2] for 19 equal temperament: intervals are notated similarly to those they approximate and there are only two enharmonic equivalents without double sharps or flats (E♯/F♭ and B♯/C♭).^[10] Play (help·info).

19-EDO can be represented with the traditional letter names and system of sharps and flats by treating flats and sharps as distinct notes; in 19-EDO only B♯ is enharmonic with C♭, and E♯ with F♭. This article will use that notation.

Interval size[]

play diatonic scale in 19 EDO (help·info), contrast with diatonic scale in 12 EDO (help·info), contrast with just diatonic scale (help·info)

Here are the sizes of some common intervals and comparison with the ratios arising in the harmonic series; the difference column measures in cents the distance from an exact fit to these ratios.

For reference, the difference from the perfect fifth in the widely used 12 TET is 1.955 cents flat, the difference from the major third is 13.686 cents sharp, the minor third is 15.643 cents flat, and the (lost) harmonic minor seventh is 31.174 cents sharp.

Interval name	Size (steps)	Size (cents)	Midi	Just ratio	Just (cents)	Midi	Error (cents)
Octave	19	1200 00		2:1	1200 00		00
Septimal major seventh	18	1136.84		27:14	1137.04		−00.20
Diminished octave	18	1136.84		48:25	1129.33	Play (help·info)	+07.51
Major seventh	17	1073.68		15:8	1088.27	Play (help·info)	−14.58
Minor seventh	16	1010.53		9:5	1017.60	Play (help·info)	−07.07
Harmonic minor seventh	15	0947.37		7:4	0968.83	Play (help·info)	−21.46
Septimal major sixth	15	0947.37		12:7	0933.13	Play (help·info)	+14.24
Major sixth	14	0884.21		5:3	0884.36	Play (help·info)	−00.15
Minor sixth	13	0821.05		8:5	0813.69	Play (help·info)	+07.37
Augmented fifth	12	0757.89		25:16	0772.63	Play (help·info)	−14.73
Septimal minor sixth	12	0757.89		14:9	0764.92		−07.02
Perfect fifth	11	0694.74	Play (help·info)	3:2	0701.96	Play (help·info)	−07.22
Greater tridecimal tritone	10	0631.58		13:90	0636.62		−05.04
Greater septimal tritone, diminished fifth	10	0631.58	Play (help·info)	10:70	0617.49	Play (help·info)	+14.09
Lesser septimal tritone, augmented fourth	09	0568.42	Play (help·info)	7:5	0582.51		−14.09
Lesser tridecimal tritone	09	0568.42		18:13	0563.38		+05.04
Perfect fourth	08	0505.26	Play (help·info)	4:3	0498.04	Play (help·info)	+07.22
Augmented third	07	0442.11		125:96	0456.99	Play (help·info)	−14.88
Tridecimal major third	07	0442.11		13:10	0454.12		−10.22
Septimal major third	07	0442.11	Play (help·info)	9:7	0435.08	Play (help·info)	+07.03
Major third	06	0378.95	Play (help·info)	5:4	0386.31	Play (help·info)	−07.36
Inverted 13th harmonic	06	0378.95		16:13	0359.47		+19.48
Minor third	05	0315.79	Play (help·info)	6:5	0315.64	Play (help·info)	+00.15
Septimal minor third	04	0252.63		7:6	0266.87	Play (help·info)	−14.24
Tridecimal 5⁄4-tone	04	0252.63		15:13	0247.74		+04.89
Septimal whole tone	04	0252.63	Play (help·info)	8:7	0231.17	Play (help·info)	+21.46
Whole tone, major tone	03	0189.47		9:8	0203.91	Play (help·info)	−14.44
Whole tone, minor tone	03	0189.47	Play (help·info)	10:90	0182.40	Play (help·info)	+07.07
Greater tridecimal 2⁄3-tone	02	0126.32		13:12	0138.57		−12.26
Lesser tridecimal 2⁄3-tone	02	0126.32		14:13	0128.30		−01.98
Septimal diatonic semitone	02	0126.32		15:14	0119.44	Play (help·info)	+06.88
Diatonic semitone, just	02	0126.32		16:15	0111.73	Play (help·info)	+14.59
Septimal chromatic semitone	01	0063.16	Play (help·info)	21:20	0084.46		−21.31
Chromatic semitone, just	01	0063.16		25:24	0070.67	Play (help·info)	−07.51
Septimal third-tone	01	0063.16	Play (help·info)	28:27	0062.96		+00.20

Scale diagram[]

Circle of fifths in 19 tone equal temperament

Major chord on C in 19 equal temperament: All notes within 8 cents of just intonation (rather than 14 for 12 equal temperament). Play 19 ET (help·info), Play just (help·info), or Play 12 ET (help·info).

Because 19 is a prime number, repeating any fixed interval in this tuning system cycles through all possible notes; just as one may cycle through 12 EDO on the circle of fifths, since a fifth is 7 semitones, and number 7 does not divide 12 evenly (7 is coprime to 12).

Modes[]

Ionian Mode (Major Scale)[]