Cent (music)

One cent compared to a semitone on a truncated monochord.

Octaves increase exponentially when measured on a linear frequency scale (Hz).

Octaves are equally spaced when measured on a logarithmic scale (cents).

The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each. Typically, cents are used to express small intervals, or to compare the sizes of comparable intervals in different tuning systems, and in fact the interval of one cent is too small to be perceived between successive notes.

Cents, as described by Alexander J. Ellis, follow a tradition of measuring intervals by logarithms that began with Juan Caramuel y Lobkowitz in the 17th century.^[a] Ellis chose to base his measures on the hundredth part of a semitone, ¹²⁰⁰√2, at Robert Holford Macdowell Bosanquet's suggestion. He made extensive measurements of musical instruments from around the world, using cents extensively to report and compare the scales employed,^[1] and further described and employed the system in his 1875 edition of Hermann von Helmholtz's On the Sensations of Tone. It has become the standard method of representing and comparing musical pitches and intervals.^[2][3]

Use[]

Comparison of equal-tempered (black) and Pythagorean (green) intervals showing the relationship between frequency ratio and the intervals' values, in cents.

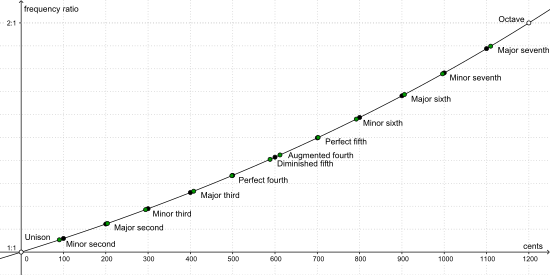
A cent is a unit of measure for the ratio between two frequencies. An equally tempered semitone (the interval between two adjacent piano keys) spans 100 cents by definition. An octave—two notes that have a frequency ratio of 2:1—spans twelve semitones and therefore 1200 cents. Since a frequency raised by one cent is simply multiplied by this constant cent value, and 1200 cents doubles a frequency, the ratio of frequencies one cent apart is precisely equal to 2^1⁄1200 = ¹²⁰⁰√2, the 1200th root of 2, which is approximately 1.0005777895.

If one knows the frequencies a and b of two notes, the number of cents measuring the interval from a to b may be calculated by the following formula (similar to the definition of a decibel):

${\displaystyle n=1200\cdot \log _{2}\left({\frac {b}{a}}\right)}$

Likewise, if one knows a note a and the number n of cents in the interval from a to b, then b may be calculated by:

${\displaystyle b=a\times 2^{\frac {n}{1200}}}$

To compare different tuning systems, convert the various interval sizes into cents. For example, in just intonation, the major third is represented by the frequency ratio 5:4. Applying the formula at the top shows that this is about 386 cents. The equivalent interval on the equal-tempered piano would be 400 cents. The difference, 14 cents, is about a seventh of a half step, easily audible.

Piecewise linear approximation[]

As x increases from 0 to 1⁄12, the function 2^x increases almost linearly from 1.00000 to 1.05946. The exponential cent scale can therefore be accurately approximated as a piecewise linear function that is numerically correct at semitones. That is, n cents for n from 0 to 100 may be approximated as 1 + 0.0005946n instead of 2^n⁄1200. The rounded error is zero when n is 0 or 100, and is about 0.72 cents high when n is 50, where the correct value of 2^1⁄24 = 1.02930 is approximated by 1 + 0.0005946 × 50 = 1.02973. This error is well below anything humanly audible, making this piecewise linear approximation adequate for most practical purposes.

Human perception[]

Waveforms of a unison (blue) versus a cent (red), nearly indistinguishable.

It is difficult to establish how many cents are perceptible to humans; this precision varies greatly from person to person. One author stated that humans can distinguish a difference in pitch of about 5–6 cents.^[4] The threshold of what is perceptible, technically known as the just noticeable difference (JND), also varies as a function of the frequency, the amplitude and the timbre. In one study, changes in tone quality reduced student musicians' ability to recognize, as out-of-tune, pitches that deviated from their appropriate values by ±12 cents.^[5] It has also been established that increased tonal context enables listeners to judge pitch more accurately.^[6] "While intervals of less than a few cents are imperceptible to the human ear in a melodic context, in harmony very small changes can cause large changes in beats and roughness of chords."^[7]

When listening to pitches with vibrato, there is evidence that humans perceive the mean frequency as the center of the pitch.^[8] One study of modern performances of Schubert's Ave Maria found that vibrato span typically ranged between ±34 cents and ±123 cents with a mean of ±71 cents and noted higher variation in Verdi's opera arias.^[9]

Normal adults are able to recognize pitch differences of as small as 25 cents very reliably. Adults with amusia, however, have trouble recognizing differences of less than 100 cents and sometimes have trouble with these or larger intervals.^[10]

Centitone[]

A centitone (also Iring) is a musical interval (2^1⁄600) equal to two cents (2^2⁄1200)^[11][12] proposed as a unit of measurement (Play (help·info)) by Widogast Iring in Die reine Stimmung in der Musik (1898) as 600 steps per octave and later by Joseph Yasser in A Theory of Evolving Tonality (1932) as 100 steps per equal tempered whole tone.

Iring noticed that the Grad/Werckmeister (1.96 cents, 12 per Pythagorean comma) and the schisma (1.95 cents) are nearly the same (≈ 614 steps per octave) and both may be approximated by 600 steps per octave (2 cents).^[13] Yasser promoted the decitone, centitone, and millitone (10, 100, and 1000 steps per whole tone = 60, 600, and 6000 steps per octave = 20, 2, and 0.2 cents).^[14][15]

For example: Equal tempered perfect fifth = 700 cents = 175.6 savarts = 583.3 millioctaves = 350 centitones.^[16]

Sound files[]

The following audio files play various intervals. In each case the first note played is middle C. The next note is sharper than C by the assigned value in cents. Finally, the two notes are played simultaneously.

Note that the JND for pitch difference is 5–6 cents. Played separately, the notes may not show an audible difference, but when they are played together, beating may be heard (for example if middle C and a note 10 cents higher are played). At any particular instant, the two waveforms reinforce or cancel each other more or less, depending on their instantaneous phase relationship. A piano tuner may verify tuning accuracy by timing the beats when two strings are sounded at once.

Play middle C & 1 cent above (help·info), beat frequency = 0.16 Hz
Play middle C & 10.06 cents above (help·info), beat frequency = 1.53 Hz
Play middle C & 25 cents above (help·info), beat frequency = 3.81 Hz

	One Cent Interval Menu 0:00 Sine wave plays at middle C, middle C 1 cent sharp, then both at the same time.
Problems playing this file? See media help.

	Twelve Cent Interval Menu 0:00 Sine wave plays at middle C, middle C 12 cents sharp, then both at the same time.
Problems playing this file? See media help.

	Twenty-four Cent Interval Menu 0:00 Sine wave plays at middle C, middle C 24 cents sharp, then both at the same time.
Problems playing this file? See media help.

See also[]

• Degree
• Equal temperament
• Gradian
• Logarithm
• Microtonal music
• Millioctave
• Radian
• Savart

References[]

Footnotes[]

Citations[]

Sources[]

External links[]

• Cent conversion: Whole number ratio to cent [rounded to whole number]
• Cent conversion: Online utility with several functions