3-4-6-12 tiling

From Wikipedia, the free encyclopedia
3-4-6-12 tiling
2-uniform n1.svg
Type 2-uniform tiling
Vertex configuration Small rhombitrihexagonal tiling vertfig.pngGreat rhombitrihexagonal tiling vertfig.png
3.4.6.4 and 4.6.12
Symmetry p6m, [6,3], (*632)
Rotation symmetry p6, [6,3]+, (632)
Properties 2-uniform, 4-isohedral, 4-isotoxal

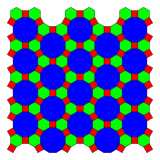
In geometry of the Euclidean plane, the 3-4-6-12 tiling is one of 20 2-uniform tilings of the Euclidean plane by regular polygons, containing regular triangles, squares, hexagons and dodecagons, arranged in two vertex configuration: 3.4.6.4 and 4.6.12.[1][2][3][4]

It has hexagonal symmetry, p6m, [6,3], (*632). It is also called a demiregular tiling by some authors.

Geometry[]

Its two vertex configurations are shared with two 1-uniform tilings:

rhombitrihexagonal tiling truncated trihexagonal tiling
1-uniform n6.svg
3.4.6.4 		1-uniform n3.svg
4.6.12

It can be seen as a type of diminished rhombitrihexagonal tiling, with dodecagons replacing periodic sets of hexagons and surrounding squares and triangles. This is similar to the Johnson solid, a diminished rhombicosidodecahedron, which is a rhombicosidodecahedron with faces removed, leading to new decagonal faces. The dual of this variant is shown to the right (deltoidal hexagonal insets).

1-uniform 6 with dodecagons.pngDual of Planar Tiling (Uniform Two 5) 4.6.12; 3.4.6.4 Corrected Variant O.png

Related k-uniform tilings of regular polygons[]

The hexagons can be dissected into 6 triangles, and the dodecagons can be dissected into triangles, hexagons and squares.

Dissected polygons
Triangular tiling vertfig.png Hexagonal cupola flat.png Dissected dodecagon.png
Hexagon Dodecagon
(each has 2 orientations)
Dual Processes (Dual 'Insets')
3-uniform tilings
48 26 18 (2-uniform)
3-uniform 48 with hexagons.png
[36; 32.4.3.4; 32.4.12] 		3-uniform 26 with dodecagons.png
[3.42.6; (3.4.6.4)2] 		2-uniform 18 with hexagons dodecagons.png
[36; 32.4.3.4]
Dual of Planar Tiling (Uniform Two 5) 4.6.12; 3.4.6.4 Corrected Variant I.png
V[36; 32.4.3.4; 32.4.12]
V[3.42.6; (3.4.6.4)2] 		Dual of Planar Tiling (Uniform Two 5) 4.6.12; 3.4.6.4 Corrected Variant III.png
V[36; 32.4.3.4]
3-uniform duals

Circle Packing[]

This 2-uniform tiling can be used as a circle packing. Cyan circles are in contact with 3 other circles (2 cyan, 1 pink), corresponding to the V4.6.12 planigon, and pink circles are in contact with 4 other circles (1 cyan, 2 pink), corresponding to the V3.4.6.4 planigon. It is homeomorphic to the ambo operation on the tiling, with the cyan and pink gap polygons corresponding to the cyan and pink circles (mini-vertex configuration polygons; one dimensional duals to the respective planigons). Both images coincide.

C[3.4.6.12] a[3.4.6.12]
Circle Packing of 2-Uniform 3.4.6.12.png Ambo Operation on 2-Uniform 3.4.6.12.png

Dual tiling[]

The dual tiling has right triangle and kite faces, defined by face configurations: V3.4.6.4 and V4.6.12, and can be seen combining the deltoidal trihexagonal tiling and kisrhombille tilings.

2-uniform 1 dual.svg
Dual tiling 		Tiling face 3-4-6-4.svg
V3.4.6.4
Tiling face 4-6-12.svg
V4.6.12 		1-uniform 6 dual.svg
Deltoidal trihexagonal tiling 		1-uniform 3 dual.svg
Kisrhombille tiling

Notes[]

  1. ^ Critchlow, pp. 62–67
  2. ^ Grünbaum and Shephard 1986, pp. 65–67
  3. ^ In Search of Demiregular Tilings #4
  4. ^ Chavey (1989)

References[]

  • Keith Critchlow, Order in Space: A design source book, 1970, pp. 62–67
  • Ghyka, M. The Geometry of Art and Life, (1946), 2nd edition, New York: Dover, 1977. Demiregular tiling #15
  • Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. pp. 35–43
  • Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman. ISBN 0-7167-1193-1. p. 65
  • Sacred Geometry Design Sourcebook: Universal Dimensional Patterns, Bruce Rawles, 1997. pp. 36–37 [1]

External links[]

Retrieved from ""