3-4 duoprism

Uniform 3-4 duoprisms 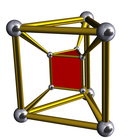Schlegel diagrams
Type	Prismatic uniform polychoron
Schläfli symbol	{3}×{4}
Coxeter-Dynkin diagram
Cells	3 square prisms, 4 triangular prisms
Faces	15 squares, 4 triangles
Edges	24
Vertices	12
Vertex figure	Digonal disphenoid
Symmetry	[3,2,4], order 48
Dual	3-4 duopyramid
Properties	convex, vertex-uniform

In geometry of 4 dimensions, a 3-4 duoprism, the second smallest p-q duoprism, is a 4-polytope resulting from the Cartesian product of a triangle and a square.

The 3-4 duoprism exists in some of the uniform 5-polytopes in the B5 family.

Images[]

Net	3D projection with 3 different rotations

Related complex polygons[]

Stereographic projection of complex polygon, ₃{}×₄{} has 12 vertices and 7 3-edges, shown here with 4 red triangular 3-edges and 3 blue square 4-edges.

The quasiregular complex polytope ₃{}×₄{}, , in $\mathbb {C} ^{2}$ has a real representation as a 3-4 duoprism in 4-dimensional space. It has 12 vertices, and 4 3-edges and 3 4-edges. Its symmetry is ₃[2]₄, order 12.^[1]

Related polytopes[]

The birectified 5-cube, has a uniform 3-4 duoprism vertex figure:

3-4 duopyramid[]

3-4 duopyramid
Type	duopyramid
Schläfli symbol	{3}+{4}
Coxeter-Dynkin diagram
Cells	12 digonal disphenoids
Faces	24 isosceles triangles
Edges	19 (12+3+4)
Vertices	7 (3+4)
Symmetry	[3,2,4], order 48
Dual	3-4 duoprism
Properties	convex, facet-transitive

The dual of a 3-4 duoprism is called a 3-4 duopyramid. It has 12 digonal disphenoid cells, 24 isosceles triangular faces, 12 edges, and 7 vertices.

Orthogonal projection	Vertex-centered perspective

Notes[]

^ Coxeter, H. S. M.; Regular Complex Polytopes, Cambridge University Press, (1974).

References[]

Regular Polytopes, H. S. M. Coxeter, Dover Publications, Inc., 1973, New York, p. 124.
Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues)
- Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proc. London Math. Soc. 43, 33–62, 1937.
John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
Catalogue of Convex Polychora, section 6, George Olshevsky.

External links[]

The Fourth Dimension Simply Explained—describes duoprisms as "double prisms" and duocylinders as "double cylinders"
Polygloss - glossary of higher-dimensional terms
Exploring Hyperspace with the Geometric Product

[1] Coxeter, H. S. M.; Regular Complex Polytopes, Cambridge University Press, (1974).

[1]