5-cell

Regular 5-cell (pentachoron) (4-simplex)
Schlegel diagram (vertices and edges)
Type	Convex regular 4-polytope
Schläfli symbol	{3,3,3}
Coxeter diagram
Cells	5 {3,3}
Faces	10 {3}
Edges	10
Vertices	5
Vertex figure	(tetrahedron)
Petrie polygon	pentagon
Coxeter group	A4, [3,3,3]
Dual	Self-dual
Properties	convex, isogonal, isotoxal, isohedral
Uniform index	1

Vertex figure: tetrahedron

Net

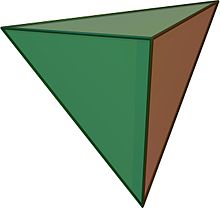
In geometry, the 5-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,3,3}. It is a four-dimensional object bounded by 5 tetrahedral cells. It is also known as a C₅, pentachoron,^[1] pentatope, pentahedroid,^[2] or tetrahedral pyramid. It is the 4-simplex (Coxeter's ${\displaystyle \alpha _{4}}$polytope^[3]), the simplest possible convex regular 4-polytope (four-dimensional analogue of a Platonic solid), and is analogous to the tetrahedron in three dimensions and the triangle in two dimensions. The pentachoron is a four dimensional pyramid with a tetrahedral base.

The regular 5-cell is bounded by 5 regular tetrahedra, and is one of the six regular convex 4-polytopes, represented by the Schläfli symbol {3,3,3}.

The 5-cell is a solution to the problem: Make 10 equilateral triangles, all of the same size, using 10 matchsticks, where each side of every triangle is exactly one matchstick. No solution exists in three dimensions.

The convex hull of two 5-cells in dual configuration is the disphenoidal 30-cell, dual of the bitruncated 5-cell.

Alternative names[]

• Pentachoron
• 4-simplex
• Pentatope
• Pentahedroid (Henry Parker Manning)
• Pen (Jonathan Bowers: for pentachoron)^[4]
• Hyperpyramid, tetrahedral pyramid

Geometry[]

The 5-cell is self-dual, and its vertex figure is a tetrahedron. Its maximal intersection with 3-dimensional space is the triangular prism. Its dihedral angle is cos⁻¹(1/4), or approximately 75.52°.

As a configuration[]

This configuration matrix represents the 5-cell. The rows and columns correspond to vertices, edges, faces, and cells. The diagonal numbers say how many of each element occur in the whole 5-cell. The nondiagonal numbers say how many of the column's element occur in or at the row's element. This self-dual polytope's matrix is identical to its 180 degree rotation.^[5]

${\displaystyle {\begin{bmatrix}{\begin{matrix}5&4&6&4\\2&10&3&3\\3&3&10&2\\4&6&4&5\end{matrix}}\end{bmatrix}}}$

Construction[]

The 5-cell can be constructed from a tetrahedron by adding a 5th vertex such that it is equidistant from all the other vertices of the tetrahedron. (The 5-cell is a 4-dimensional pyramid with a tetrahedral base and four tetrahedral sides.)

The simplest set of coordinates is: (2,0,0,0), (0,2,0,0), (0,0,2,0), (0,0,0,2), (φ,φ,φ,φ), with edge length 2√2, where φ is the golden ratio.^[6]

The Cartesian coordinates of the vertices of an origin-centered regular 5-cell having edge length 2 and radius √1.6 are:

${\displaystyle \left({\frac {1}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {1}{\sqrt {3}}},\ \pm 1\right)}$

${\displaystyle \left({\frac {1}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {-2}{\sqrt {3}}},\ 0\right)}$

${\displaystyle \left({\frac {1}{\sqrt {10}}},\ -{\sqrt {\frac {3}{2}}},\ 0,\ 0\right)}$

${\displaystyle \left(-2{\sqrt {\frac {2}{5}}},\ 0,\ 0,\ 0\right)}$

Another set of origin-centered coordinates in 4-space can be seen as a hyperpyramid with a regular tetrahedral base in 3-space, with edge length 2√2 and radius √3.2:

${\displaystyle \left(1,1,1,{\frac {-1}{\sqrt {5}}}\right)}$

${\displaystyle \left(1,-1,-1,{\frac {-1}{\sqrt {5}}}\right)}$

${\displaystyle \left(-1,1,-1,{\frac {-1}{\sqrt {5}}}\right)}$

${\displaystyle \left(-1,-1,1,{\frac {-1}{\sqrt {5}}}\right)}$

${\displaystyle \left(0,0,0,{\frac {4}{\sqrt {5}}}\right)}$

The vertices of a 4-simplex (with edge √2 and radius 1) can be more simply constructed on a hyperplane in 5-space, as (distinct) permutations of (0,0,0,0,1) or (0,1,1,1,1); in these positions it is a facet of, respectively, the 5-orthoplex or the rectified penteract.

Boerdijk–Coxeter helix[]

A 5-cell can be constructed as a Boerdijk–Coxeter helix of five chained tetrahedra, folded into a 4-dimensional ring. The 10 triangle faces can be seen in a 2D net within a triangular tiling, with 6 triangles around every vertex, although folding into 4-dimensions causes edges to coincide. The purple edges represent the Petrie polygon of the 5-cell.

Projections[]

The A₄ Coxeter plane projects the 5-cell into a regular pentagon and pentagram. The A₃ Coxeter plane projection of the 5-cell is that of a square pyramid. The A₂ Coxeter plane projection of the regular 5-cell is that of a triangular bipyramid (two tetrahedra joined face-to-face) with the two opposite vertices centered.

orthographic projections

Ak Coxeter plane	A4	A3	A2
Graph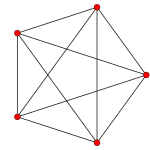
Dihedral symmetry	[5]	[4]	[3]

Projections to 3 dimensions
Stereographic projection wireframe (edge projected onto a 3-sphere)	A 3D projection of a 5-cell performing a simple rotation
The vertex-first projection of the 5-cell into 3 dimensions has a tetrahedral projection envelope. The closest vertex of the 5-cell projects to the center of the tetrahedron, as shown here in red. The farthest cell projects onto the tetrahedral envelope itself, while the other 4 cells project onto the 4 flattened tetrahedral regions surrounding the central vertex.	The edge-first projection of the 5-cell into 3 dimensions has a triangular dipyramidal envelope. The closest edge (shown here in red) projects to the axis of the dipyramid, with the three cells surrounding it projecting to 3 tetrahedral volumes arranged around this axis at 120 degrees to each other. The remaining 2 cells project to the two halves of the dipyramid and are on the far side of the pentatope.
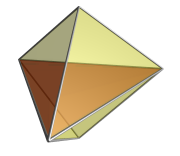The face-first projection of the 5-cell into 3 dimensions also has a triangular dipyramidal envelope. The nearest face is shown here in red. The two cells that meet at this face project to the two halves of the dipyramid. The remaining three cells are on the far side of the pentatope from the 4D viewpoint, and are culled from the image for clarity. They are arranged around the central axis of the dipyramid, just as in the edge-first projection.	The cell-first projection of the 5-cell into 3 dimensions has a tetrahedral envelope. The nearest cell projects onto the entire envelope, and, from the 4D viewpoint, obscures the other 4 cells; hence, they are not rendered here.

Irregular 5-cell[]

There are many lower symmetry forms, including these found in uniform polytope vertex figures:

Symmetry	[3,3,3] Order 120	[3,3,1] Order 24	[3,2,1] Order 12	[3,1,1] Order 6	[5,2]+ Order 10
Name	Regular 5-cell	Tetrahedral pyramid	Triangular-pyramidal pyramid		Pentagonal hyperdisphenoid
Schläfli	{3,3,3}	{3,3} ∨ ( )	{3} ∨ { }	{3} ∨ ( ) ∨ ( )
Example Vertex figure	5-simplex	Truncated 5-simplex	Bitruncated 5-simplex	Cantitruncated 5-simplex	Omnitruncated 4-simplex honeycomb

The tetrahedral pyramid is a special case of a 5-cell, a polyhedral pyramid, constructed as a regular tetrahedron base in a 3-space hyperplane, and an apex point above the hyperplane. The four sides of the pyramid are made of tetrahedron cells.

Many uniform 5-polytopes have tetrahedral pyramid vertex figures:

Symmetry [3,3,1], order 24

Schlegel diagram
Name Coxeter	{ }×{3,3,3}	{ }×{4,3,3}		t{3,3,3,3}	t{4,3,3,3}	t{3,4,3,3}

Other uniform 5-polytopes have irregular 5-cell vertex figures. The symmetry of a vertex figure of a uniform polytope is represented by removing the ringed nodes of the Coxeter diagram.

Symmetry	[3,2,1], order 12		[3,1,1], order 6		[2+,4,1], order 8	[2,1,1], order 4
Schlegel diagram
Name Coxeter	t12α5	t12γ5	t012α5	t012γ5	t123α5	t123γ5

Symmetry	[2,1,1], order 2			[2+,1,1], order 2	[ ]+, order 1
Schlegel diagram
Name Coxeter	t0123α5	t0123γ5	t0123β5	t01234α5	t01234γ5

Compound[]

The compound of two 5-cells in dual configurations can be seen in this A5 Coxeter plane projection, with a red and blue 5-cell vertices and edges. This compound has [[3,3,3]] symmetry, order 240. The intersection of these two 5-cells is a uniform bitruncated 5-cell. = ∩ .

This compound can be seen as the 4D analogue of the 2D hexagram {6/2} and the 3D compound of two tetrahedra.

Related polytopes and honeycombs[]

The 5-cell is the first in the sequence of 6 convex regular 4-polytopes (in order of size and complexity).

Regular convex 4-polytopes
Symmetry group	A4	B4		F4	H4
Name	5-cell Hyper- tetrahedron	16-cell Hyper- octahedron	8-cell Hyper- cube	24-cell	600-cell Hyper- icosahedron	120-cell Hyper- dodecahedron
Schläfli symbol	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
Coxeter diagram
Graph
Vertices	5	8	16	24	120	600
Edges	10	24	32	96	720	1200
Faces	10 triangles	32 triangles	24 squares	96 triangles	1200 triangles	720 pentagons
Cells	5 tetrahedra	16 tetrahedra	8 cubes	24 octahedra	600 tetrahedra	120 dodecahedra
Tori	1 5-tetrahedron	2 8-tetrahedron	2 4-cube	4 6-octahedron	20 30-tetrahedron	12 10-dodecahedron
Inscribed	120 in 120-cell	1 16-cell	2 16-cells	3 8-cells	5 24-cells x 5	5 600-cells x 2
Great polygons		2