Area of a circle

Geometry
Projecting a sphere to a plane
Outline History
Branches Euclidean Non-Euclidean Elliptic Spherical Hyperbolic Non-Archimedean geometry Projective Affine Synthetic Analytic Algebraic Arithmetic Diophantine Differential Riemannian Symplectic Discrete differential Complex Finite Discrete/Combinatorial Digital Convex Computational Fractal Incidence Noncommutative geometry Noncommutative algebraic geometry
Concepts Features Dimension Straightedge and compass constructions Angle Curve Diagonal Orthogonality (Perpendicular) Parallel Vertex Congruence Similarity Symmetry
Zero-dimensional Point
One-dimensional Line segment ray Length
Two-dimensional Plane Area Polygon Triangle Altitude Hypotenuse Pythagorean theorem Parallelogram Square Rectangle Rhombus Rhomboid Quadrilateral Trapezoid Kite Circle Diameter Circumference Area
Three-dimensional Volume Cube cuboid Cylinder Pyramid Sphere
Four- / other-dimensional Tesseract Hypersphere
Geometers
by name Aida Aryabhata Ahmes Alhazen Apollonius Archimedes Atiyah Baudhayana Bolyai Brahmagupta Cartan Coxeter Descartes Euclid Euler Gauss Gromov Hilbert Jyeṣṭhadeva Kātyāyana Khayyám Klein Lobachevsky Manava Minkowski Minggatu Pascal Pythagoras Parameshvara Poincaré Riemann Sakabe Sijzi al-Tusi Veblen Virasena Yang Hui al-Yasamin Zhang List of geometers
by period BCE Ahmes Baudhayana Manava Pythagoras Euclid Archimedes Apollonius 1–1400s Zhang Kātyāyana Aryabhata Brahmagupta Virasena Alhazen Sijzi Khayyám al-Yasamin al-Tusi Yang Hui Parameshvara 1400s–1700s Jyeṣṭhadeva Descartes Pascal Minggatu Euler Sakabe Aida 1700s–1900s Gauss Lobachevsky Bolyai Riemann Klein Poincaré Hilbert Minkowski Cartan Veblen Coxeter Present day Atiyah Gromov
v t

In geometry, the area enclosed by a circle of radius r is πr². Here the Greek letter π represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 3.1416.

One method of deriving this formula, which originated with Archimedes, involves viewing the circle as the limit of a sequence of regular polygons. The area of a regular polygon is half its perimeter multiplied by the distance from its center to its sides, and the corresponding formula–that the area is half the perimeter times the radius–namely, A = 1/2 × 2πr × r, holds in the limit for a circle.

History[]

Modern mathematics can obtain the area using the methods of integral calculus or its more sophisticated offspring, real analysis. However, the area of a disk was studied by the Ancient Greeks. Eudoxus of Cnidus in the fifth century B.C. had found that the area of a disk is proportional to its radius squared.^[1] Archimedes used the tools of Euclidean geometry to show that the area inside a circle is equal to that of a right triangle whose base has the length of the circle's circumference and whose height equals the circle's radius in his book Measurement of a Circle. The circumference is 2πr, and the area of a triangle is half the base times the height, yielding the area π r² for the disk. Prior to Archimedes, Hippocrates of Chios was the first to show that the area of a disk is proportional to the square of its diameter, as part of his quadrature of the lune of Hippocrates,^[2] but did not identify the constant of proportionality.

Historical arguments[]

A variety of arguments have been advanced historically to establish the equation ${\displaystyle A=\pi r^{2}}$ to varying degrees of mathematical rigor. The most famous of these is Archimedes' method of exhaustion, one of the earliest uses of the mathematical concept of a limit, as well as the origin of Archimedes' axiom which remains part of the standard analytical treatment of the real number system. The original proof of Archimedes is not rigorous by modern standards, because it assumes that we can compare the length of arc of a circle to the length of a secant and a tangent line, and similar statements about the area, as geometrically evident.

Using polygons[]

The area of a regular polygon is half its perimeter times the apothem. As the number of sides of the regular polygon increases, the polygon tends to a circle, and the apothem tends to the radius. This suggests that the area of a disk is half the circumference of its bounding circle times the radius.^[3]

Archimedes's proof[]

Following Archimedes' argument in The Measurement of a Circle (c. 260 BCE), compare the area enclosed by a circle to a right triangle whose base has the length of the circle's circumference and whose height equals the circle's radius. If the area of the circle is not equal to that of the triangle, then it must be either greater or less. We eliminate each of these by contradiction, leaving equality as the only possibility. We use regular polygons in the same way.

Not greater[]

Circle with square and octagon inscribed, showing area gap

Suppose that the area C enclosed by the circle is greater than the area T = ¹⁄₂cr of the triangle. Let E denote the excess amount. Inscribe a square in the circle, so that its four corners lie on the circle. Between the square and the circle are four segments. If the total area of those gaps, G₄, is greater than E, split each arc in half. This makes the inscribed square into an inscribed octagon, and produces eight segments with a smaller total gap, G₈. Continue splitting until the total gap area, G_n, is less than E. Now the area of the inscribed polygon, P_n = C − G_n, must be greater than that of the triangle.

${\displaystyle {\begin{aligned}E&{}=C-T\\&{}>G_{n}\\P_{n}&{}=C-G_{n}\\&{}>C-E\\P_{n}&{}>T\end{aligned}}}$

But this forces a contradiction, as follows. Draw a perpendicular from the center to the midpoint of a side of the polygon; its length, h, is less than the circle radius. Also, let each side of the polygon have length s; then the sum of the sides, ns, is less than the circle circumference. The polygon area consists of n equal triangles with height h and base s, thus equals ¹⁄₂nhs. But since h < r and ns < c, the polygon area must be less than the triangle area, ¹⁄₂cr, a contradiction. Therefore, our supposition that C might be greater than T must be wrong.

Not less[]

Circle with square and octagon circumscribed, showing area gap

Suppose that the area enclosed by the circle is less than the area T of the triangle. Let D denote the deficit amount. Circumscribe a square, so that the midpoint of each edge lies on the circle. If the total area gap between the square and the circle, G₄, is greater than D, slice off the corners with circle tangents to make a circumscribed octagon, and continue slicing until the gap area is less than D. The area of the polygon, P_n, must be less than T.

${\displaystyle {\begin{aligned}D&{}=T-C\\&{}>G_{n}\\P_{n}&{}=C+G_{n}\\&{}<C+D\\P_{n}&{}<T\end{aligned}}}$

This, too, forces a contradiction. For, a perpendicular to the midpoint of each polygon side is a radius, of length r. And since the total side length is greater than the circumference, the polygon consists of n identical triangles with total area greater than T. Again we have a contradiction, so our supposition that C might be less than T must be wrong as well.

Therefore, it must be the case that the area enclosed by the circle is precisely the same as the area of the triangle. This concludes the proof.

Rearrangement proof[]

Circle area by rearrangement

Graphs of side, s; apothem, a; and area, A of regular polygons of n sides and circumradius 1, with the base, b of a rectangle with the same area. The green line shows the case n = 6.

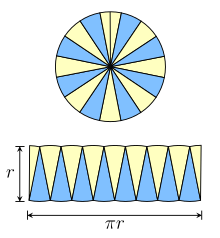
Following Satō Moshun (Smith & Mikami 1914, pp. 130–132) and Leonardo da Vinci (Beckmann 1976, p. 19), we can use inscribed regular polygons in a different way. Suppose we inscribe a hexagon. Cut the hexagon into six triangles by splitting it from the center. Two opposite triangles both touch two common diameters; slide them along one so the radial edges are adjacent. They now form a parallelogram, with the hexagon sides making two opposite edges, one of which is the base, s. Two radial edges form slanted sides, and the height, h is equal to its apothem (as in the Archimedes proof). In fact, we can also assemble all the triangles into one big parallelogram by putting successive pairs next to each other. The same is true if we increase it to eight sides and so on. For a polygon with 2n sides, the parallelogram will have a base of length ns, and a height h. As the number of sides increases, the length of the parallelogram base approaches half the circle circumference, and its height approaches the circle radius. In the limit, the parallelogram becomes a rectangle with width πr and height r.

Unit disk area by rearranging n polygons.

polygon			parallelogram
n	side		base	height	area
4	1.4142136		2.8284271	0.7071068	2.0000000
6	1.0000000		3.0000000	0.8660254	2.5980762
8	0.7653669		3.0614675	0.9238795	2.8284271
10	0.6180340		3.0901699	0.9510565	2.9389263
12	0.5176381		3.1058285	0.9659258	3.0000000
14	0.4450419		3.1152931	0.9749279	3.0371862
16	0.3901806		3.1214452	0.9807853	3.0614675
96	0.0654382		3.1410320	0.9994646	3.1393502
∞	1/∞		π	1	π

Modern proofs[]

There are various equivalent definitions of the constant π. The conventional definition in pre-calculus geometry is the ratio of the circumference of a circle to its diameter:

${\displaystyle \pi ={\frac {C}{D}}.}$

However, because the circumference of a circle is not a primitive analytical concept, this definition is not suitable in modern rigorous treatments. A standard modern definition is that π is equal to twice the least positive root of the cosine function or, equivalently, the half-period of the sine (or cosine) function. The cosine function can be defined either as a power series, or as the solution of a certain differential equation. This avoids any reference to circles in the definition of π, so that statements about the relation of π to the circumference and area of circles are actually theorems, rather than definitions, that follow from the analytical definitions of concepts like "area" and "circumference".

The analytical definitions are seen to be equivalent, if it is agreed that the circumference of the circle is measured as a rectifiable curve by means of the integral

${\displaystyle C=2\int _{-R}^{R}{\frac {R\,dx}{\sqrt {R^{2}-x^{2}}}}=2R\int _{-1}^{1}{\frac {dx}{\sqrt {1-x^{2}}}}.}$

The integral appearing on the right is an abelian integral whose value is a half-period of the sine function, equal to π. Thus ${\displaystyle C=2\pi R=\pi D}$ is seen to be true as a theorem.

Several of the arguments that follow use only concepts from elementary calculus to reproduce the formula ${\displaystyle A=\pi r^{2}}$, but in many cases to regard these as actual proofs, they rely implicitly on the fact that one can develop trigonometric functions and the fundamental constant π in a way that is totally independent of their relation to geometry. We have indicated where appropriate how each of these proofs can be made totally independent of all trigonometry, but in some cases that requires more sophisticated mathematical ideas than those afforded by elementary calculus.

Onion proof[]

Area of the disk via ring integration

Using calculus, we can sum the area incrementally, partitioning the disk into thin concentric rings like the layers of an onion. This is the method of shell integration in two dimensions. For an infinitesimally thin ring of the "onion" of radius t, the accumulated area is 2πt dt, the circumferential length of the ring times its infinitesimal width (one can approximate this ring by a rectangle with width=2πt and height=dt). This gives an elementary integral for a disk of radius r.

${\displaystyle {\begin{aligned}\mathrm {Area} (r)&{}=\int _{0}^{r}2\pi t\,dt\\&{}=2\pi \left[{\frac {t^{2}}{2}}\right]_{0}^{r}\\&{}=\pi r^{2}.\end{aligned}}}$

It is rigorously justified by the multivariate substitution rule in polar coordinates. Namely, the area is given by a double integral of the constant function 1 over the disk itself. If D denotes the disk, then the double integral can be computed in polar coordinates as follows:

${\displaystyle {\begin{aligned}\mathrm {Area} (r)&{}=\iint _{D}1\ d(x,y)\\&{}=\iint _{D}t\ dt\ d\theta \\&{}=\int _{0}^{r}\int _{0}^{2\pi }t\ d\theta \ dt\\&{}=\int _{0}^{r}\left[t\theta \right]_{0}^{2\pi }dt\\&{}=\int _{0}^{r}2\pi t\,dt\\\end{aligned}}}$

which is the same result as obtained above.

An equivalent rigorous justification, without relying on the special coordinates of trigonometry, uses the coarea formula. Define a function ${\displaystyle \rho :\mathbb {R} ^{2}\to \mathbb {R} }$ by ${\displaystyle \rho (x,y)={\sqrt {x^{2}+y^{2}}}}$. Note ρ is a Lipschitz function whose gradient is a unit vector ${\displaystyle |\nabla \rho |=1}$ (almost everywhere). Let D be the disc ${\displaystyle \rho <1}$ in ${\displaystyle \mathbb {R} ^{2}}$. We will show that ${\displaystyle {\mathcal {L}}^{2}(D)=\pi }$, where ${\displaystyle {\mathcal {L}}^{2}}$ is the two-dimensional Lebesgue measure in ${\displaystyle \mathbb {R} ^{2}}$. We shall assume that the one-dimensional Hausdorff measure of the circle ${\displaystyle \rho =r}$ is ${\displaystyle 2\pi r}$, the circumference of the circle of radius r. (This can be taken as the definition of circumference.) Then, by the coarea formula,

${\displaystyle {\begin{aligned}{\mathcal {L}}^{2}(D)&=\iint _{D}|\nabla \rho |\,d{\mathcal {L}}^{2}\\&=\int _{\mathbb {R} }{\mathcal {H}}^{1}(\rho ^{-1}(r)\cap D)\,dr\\&=\int _{0}^{1}{\mathcal {H}}^{1}(\rho ^{-1}(r))\,dr\\&=\int _{0}^{1}2\pi r\,dr=\pi .\end{aligned}}}$

Triangle proof[]

Circle unwrapped to form a triangle

The circle and the triangle are equal in area.

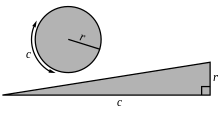
Similar to the onion proof outlined above, we could exploit calculus in a different way in order to arrive at the formula for the area of a disk. Consider unwrapping the concentric circles to straight strips. This will form a right angled triangle with r as its height and 2πr (being the outer slice of onion) as its base.

Finding the area of this triangle will give the area of the disk

${\displaystyle {\begin{aligned}{\text{Area}}&{}={\frac {1}{2}}\cdot {\text{base}}\cdot {\text{height}}\\&{}={\frac {1}{2}}\cdot 2\pi r\cdot r\\&{}=\pi r^{2}\end{aligned}}}$

The opposite and adjacent angles for this triangle are respectively in degrees 9.0430611..., 80.956939... and in radians 0.1578311... OEIS: A233527, 1.4129651...OEIS: A233528.

Explicitly, we imagine dividing up a circle into triangles, each with a height equal to the circle's radius and a base that is infinitesimally small. The area of each of these triangles is equal to ${\displaystyle 1/2\cdot r\cdot du}$. By summing up (integrating) all of the areas of these triangles, we arrive at the formula for the circle's area:

${\displaystyle {\begin{aligned}\mathrm {Area} (r)&{}=\int _{0}^{2\pi r}{\frac {1}{2}}r\,du\\&{}=\left[{\frac {1}{2}}ru\right]_{0}^{2\pi r}\\&{}=\pi r^{2}.\end{aligned}}}$

It too can be justified by a double integral of the constant function 1 over the disk by reversing the order of integration and using a change of variables in the above iterated integral:

${\displaystyle {\begin{aligned}\mathrm {Area} (r)&{}=\iint _{D}1\ d(x,y)\\&{}=\iint _{D}t\ dt\ d\theta \\&{}=\int _{0}^{2\pi }\int _{0}^{r}t\ dt\ d\theta \\&{}=\int _{0}^{2\pi }{\frac {1}{2}}r^{2}\ d\theta \\\end{aligned}}}$

Making the substitution ${\displaystyle u=r\theta ,\ du=r\ d\theta }$ converts the integral to

${\displaystyle {\begin{aligned}\int _{0}^{2\pi r}{\frac {1}{2}}{\frac {r^{2}}{r}}du=\int _{0}^{2\pi r}{\frac {1}{2}}r\ du\end{aligned}}}$

which is the same as the above result.

The triangle proof can be reformulated as an application of Green's theorem in flux-divergence form (i.e. a two-dimensional version of the divergence theorem), in a way that avoids all mention of trigonometry and the constant π. Consider the vector field ${\displaystyle \mathbf {r} =x\mathbf {i} +y\mathbf {j} }$ in the plane. So the divergence of r is equal to two, and hence the area of a disc D is equal to

${\displaystyle A={\frac {1}{2}}\iint _{D}\operatorname {div} \mathbf {r} \,dA.}$

By Green's theorem, this is the same as the outward flux of r across the circle bounding D:

${\displaystyle A={\frac {1}{2}}\oint _{\partial D}\mathbf {r} \cdot \mathbf {n} \,ds}$

where n is the unit normal and ds is the arc length measure. For a circle of radius R centered at the origin, we have ${\displaystyle |\mathbf {r} |=R}$ and ${\displaystyle \mathbf {n} =\mathbf {r} /R}$, so the above equality is

${\displaystyle A={\frac {1}{2}}\oint _{\partial D}\mathbf {r} \cdot {\frac {\mathbf {r} }{R}}\,ds={\frac {R}{2}}\oint _{\partial D}\,ds.}$

The integral of ds over the whole circle ${\displaystyle \partial D}$ is just the arc length, which is its circumference, so this shows that the area A enclosed by the circle is equal to ${\displaystyle R/2}$ times the circumference of the circle.

Another proof that uses triangles considers the area enclosed by a circle to be made up of an infinite number of triangles (i.e. the triangles each have an angle of d