Augmented triangular prism

Augmented triangular prism
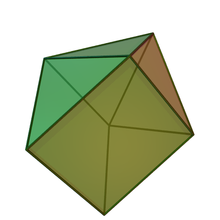Type	Johnson J48 - J49 - J50
Faces	3x2 triangles 2 squares
Edges	13
Vertices	7
Vertex configuration	2(3.42) 1(34) 4(33.4)
Symmetry group	C2v
Dual polyhedron	monolaterotruncated triangular bipyramid
Properties	convex
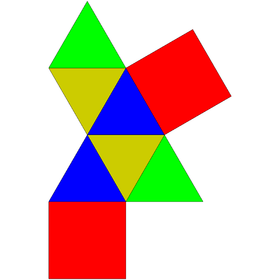
Net

In geometry, the augmented triangular prism is one of the Johnson solids (J₄₉). As the name suggests, it can be constructed by augmenting a triangular prism by attaching a square pyramid (J₁) to one of its equatorial faces. The resulting solid bears a superficial resemblance to the gyrobifastigium (J₂₆), the difference being that the latter is constructed by attaching a second triangular prism, rather than a square pyramid.

It is also the vertex figure of the nonuniform 2-p duoantiprism (if p is greater than 2). Despite the fact that p = 3 would yield a geometrically identical equivalent to the Johnson solid, it lacks a circumscribed sphere that touches all vertices.

Its dual, a triangular bipyramid with one of its 4-valence vertices truncated, can be found as cells of the 2-p duoantitegums (duals of the 2-p duoantiprisms).

A Johnson solid is one of 92 strictly convex polyhedra that is composed of regular polygon faces but are not uniform polyhedra (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.^[1]

External links[]

• Weisstein, Eric W. "Johnson Solid". MathWorld.
  • Weisstein, Eric W. "Augmented triangular prism". MathWorld.

This polyhedron-related article is a stub. You can help Wikipedia by .

• v
• t