Antiprism

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (January 2013) (Learn how and when to remove this template message)

Set of uniform n-gonal antiprisms
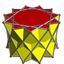
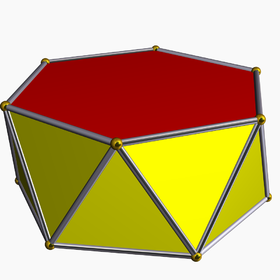Example uniform hexagonal antiprism
Type	uniform in the sense of semiregular polyhedron
Faces	2{n} + 2n{3}
Edges	4n
Vertices	2n
Conway polyhedron notation	An
Vertex configuration	3.3.3.n
Schläfli symbol	{ }⊗{n}[1] s{2,2n} sr{2,n}
Coxeter diagrams
Symmetry group	Dnd, [2+,2n], (2*n), order 4n
Rotation group	Dn, [2,n]+, (22n), order 2n
Dual polyhedron	convex dual-uniform n-gonal trapezohedron
Properties	convex, vertex-transitive, regular polygon faces, congruent & coaxial bases
Net	Example uniform enneagonal antiprism net (n = 9)

In geometry, an n-gonal antiprism or n-antiprism is a polyhedron composed of two parallel direct copies (not mirror images) of an n-sided polygon, connected by an alternating band of 2n triangles.

Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron.

Antiprisms are similar to prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are 2n triangles, rather than n quadrilaterals.

History[]

At the intersection of modern-day graph theory and coding theory, the triangulation of a set of points have interested mathematicians since Isaac Newton, who fruitlessly sought a mathematical proof of the kissing number problem in 1694.^[2] The existence of antiprisms was discussed and their name was coined by Johannes Kepler, though it is possible that they were previously known to Archimedes, as they satisfy the same conditions on faces and on vertices as the Archimedean solids.^{[citation needed]} According to Ericson and Zinoviev, HSM Coxeter (1907-2003) wrote at length on the topic,^[2] and was among the first to apply the mathematics of Victor Schlegel to this field.

Knowledge in this field is "quite incomplete" and "was obtained fairly recently", ie in the 20th century. For example, as of 2001 it was proven for only a limited number of non-trivial cases that the in the sense of minimizing the between any two points on the set: in 1943 by László Fejes Tóth for 3, 4, 6 and 12 points; in 1951 by Schütte and van Der Waerden for 5, 7, 8, 9 points; in 1965 by Danzer for 10 and 11 points; and in 1961 by Robinson for 24 points.^[2]

The chemical structure of binary compounds has been remarked to be in the family of antiprisms;^[3] especially those of the family of boron hydrides in 1975, and carboranes because they are isoelectronic. This is a mathematically real conclusion reached by studies of X-ray diffraction patterns,^[4] and stems from the 1971 work of Kenneth Wade,^[5] the nominative source for Wade's rules of Polyhedral skeletal electron pair theory.

Rare earth metals such as the lanthanides form antiprismal compounds with some of the halides or some of the iodides. The study of crystallography is useful here.^[6] Some lanthanides, when arranged in peculiar antiprismal structures with chlorine and water, can form molecule-based magnets.^[7]

Right antiprism[]

For an antiprism with regular n-gon bases, one usually considers the case where these two copies are twisted by an angle of 180/n degrees.

The axis of a regular polygon is the line perpendicular to the polygon plane and lying in the polygon centre.

For an antiprism with congruent regular n-gon bases, twisted by an angle of 180/n degrees, more regularity is obtained if the bases have the same axis: are coaxial; i.e. (for non-coplanar bases): if the line connecting the base centers is perpendicular to the base planes. Then, the antiprism is called a right antiprism, and its 2n side faces are isosceles triangles.

Uniform antiprism[]

A uniform antiprism has two congruent regular n-gon base faces, and 2n equilateral triangles as side faces.

Uniform antiprisms form an infinite class of vertex-transitive polyhedra, as do uniform prisms. For n = 2, we have the regular tetrahedron as a digonal antiprism (degenerate antiprism); for n = 3, the regular octahedron as a triangular antiprism (non-degenerate antiprism).

The dual polyhedra of the antiprisms are the trapezohedra.

Family of uniform n-gonal antiprisms

• v

Antiprism name	Digonal antiprism	(Trigonal) Triangular antiprism	(Tetragonal) Square antiprism	Pentagonal antiprism	Hexagonal antiprism	Heptagonal antiprism	Octagonal antiprism	Enneagonal antiprism	Decagonal antiprism	Hendecagonal antiprism	Dodecagonal antiprism	...	Apeirogonal antiprism
Polyhedron image												...
Spherical tiling image												Plane tiling image
Vertex config.	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	...	∞.3.3.3

Schlegel diagrams[]

A3

A4

A5

A6

A7

A8

Cartesian coordinates[]

Cartesian coordinates for the vertices of a right antiprism (i.e. with regular n-gon bases and isosceles side faces) are

${\displaystyle \left(\cos {\frac {k\pi }{n}},\sin {\frac {k\pi }{n}},(-1)^{k}h\right)}$

with k ranging from 0 to 2n – 1;

if the triangles are equilateral, then

${\displaystyle 2h^{2}=\cos {\frac {\pi }{n}}-\cos {\frac {2\pi }{n}}.}$

Volume and surface area[]

Let a be the edge-length of a uniform antiprism; then the volume is

${\displaystyle V={\frac {n{\sqrt {4\cos ^{2}{\frac {\pi }{2n}}-1}}\sin {\frac {3\pi }{2n}}}{12\sin ^{2}{\frac {\pi }{n}}}}~a^{3},}$

and the surface area is

${\displaystyle A={\frac {n}{2}}\left(\cot {\frac {\pi }{n}}+{\sqrt {3}}\right)a^{2}.}$

Related polyhedra[]

There are an infinite set of truncated antiprisms, including a lower-symmetry form of the truncated octahedron (truncated triangular antiprism). These can be alternated to create snub antiprisms, two of which are Johnson solids, and the snub triangular antiprism is a lower symmetry form of the icosahedron.

Antiprisms
				...
s{2,4}	s{2,6}	s{2,8}	s{2,10}	s{2,2n}
Truncated antiprisms
				...
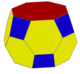
ts{2,4}	ts{2,6}	ts{2,8}	ts{2,10}	ts{2,2n}
Snub antiprisms
J84	Icosahedron	J85	Irregular faces...
				...
ss{2,4}	ss{2,6}	ss{2,8}	ss{2,10}	ss{2,2n}

Symmetry[]

The symmetry group of a right n-antiprism (i.e. with regular bases and isosceles side faces) is D_nd of order 4n, except in the cases of:

• n = 2: the regular tetrahedron, which has the larger symmetry group T_d of order 24 = 3×(4×2), which has three versions of D_2d as subgroups;

• n = 3: the regular octahedron, which has the larger symmetry group O_h of order 48 = 4×(4×3), which has four versions of D_3d as subgroups.

The symmetry group contains inversion if and only if n is odd.

The rotation group is D_n of order 2n, except in the cases of:

• n = 2: the regular tetrahedron, which has the larger rotation group T of order 12 = 3×(2×2), which has three versions of D₂ as subgroups;

• n = 3: the regular octahedron, which has the larger rotation group O of order 24 = 4×(2×3), which has four versions of D₃ as subgroups.

Star antiprism[]

5/2-antiprism			5/3-antiprism
9/2-antiprism		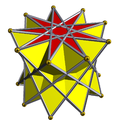9/4-antiprism		9/5-antiprism

This shows all the non-star and star antiprisms up to 15 sides - together with those of an icosikaienneagon.

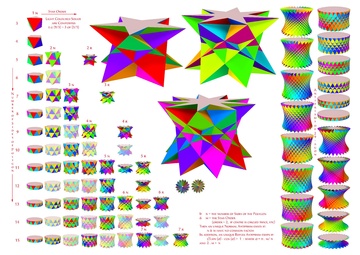
Uniform star antiprisms are named by their star polygon bases, {p/q}, and exist in prograde and in retrograde (crossed) solutions. Crossed forms have intersecting vertex figures, and are denoted by "inverted" fractions: p/(p – q) instead of p/q; example: 5/3 instead of 5/2.

A right star antiprism has two congruent coaxial regular convex or star polygon base faces, and 2n isosceles triangle side faces.

Any star antiprism with regular convex or star polygon bases can be made a right star antiprism (by translating and/or twisting one of its bases, if necessary).

In the retrograde forms but not in the prograde forms, the triangles joining the convex or star bases intersect the axis of rotational symmetry. Thus:

• Retrograde star antiprisms with regular convex polygon bases cannot have all equal edge lengths, so cannot be uniform. "Exception": a retrograde star antiprism with equilateral triangle bases (vertex configuration: 3.3/2.3.3) can be uniform; but then, it has the appearance of an equilateral triangle: it is a degenerate star polyhedron.

• Similarly, some retrograde star antiprisms with regular star polygon bases cannot have all equal edge lengths, so cannot be uniform. Example: a retrograde star antiprism with regular star 7/5-gon bases (vertex configuration: 3.3.3.7/5) cannot be uniform.

Also, star antiprism compounds with regular star p/q-gon bases can be constructed if p and q have common factors. Example: a star 10/4-antiprism is the compound of two star 5/2-antiprisms.

Star p/q-antiprisms by symmetry, for p ≤ 12

Symmetry group	Uniform stars				Right stars
D4d [2+,8] (2*4)					3.3/2.3.4
D5h [2,5] (*225)	3.3.3.5/2				3.3/2.3.5
D5d [2+,10] (2*5)	3.3.3.5/3
D6d [2+,12] (2*6)					3.3/2.3.6
D7h [2,7] (*227)	3.3.3.7/2	3.3.3.7/4
D7d [2+,14] (2*7)	3.3.3.7/3
D8d [2+,16] (2*8)	3.3.3.8/3	3.3.3.8/5
D9h [2,9] (*229)	3.3.3.9/2	3.3.3.9/4
D9d [2+,18] (2*9)	3.3.3.9/5
D10d [2+,20] (2*10)	3.3.3.10/3
D11h [2,11] (*2.2.11)	3.3.3.11/2	3.3.3.11/4	3.3.3.11/6
D11d [2+,22] (2*11)	3.3.3.11/3	3.3.3.11/5	3.3.3.11/7
D12d [2+,24] (2*12)	3.3.3.12/5	3.3.3.12/7
...	...

See also[]

• Apeirogonal antiprism
• Grand antiprism – a four-dimensional polytope
• One World Trade Center, a building consisting primarily of an elongated square antiprism
• Skew polygon

References[]

Bibliography[]

• Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. Chapter 2: Archimedean polyhedra, prisms and antiprisms

External links[]

Wikimedia Commons has media related to Antiprisms.

• Weisstein, Eric W. "Antiprism". MathWorld.
• Nonconvex Prisms and Antiprisms
• Paper models of prisms and antiprisms