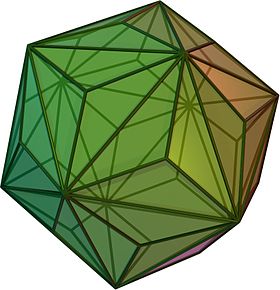
Triakis icosahedron

Triakis icosahedron
(Click here for rotating model)
Type	Catalan solid
Coxeter diagram
Conway notation	kI
Face type	V3.10.10 isosceles triangle
Faces	60
Edges	90
Vertices	32
Vertices by type	20{3}+12{10}
Symmetry group	Ih, H3, [5,3], (*532)
Rotation group	I, [5,3]+, (532)
Dihedral angle	160°36′45″ arccos(−24 + 15√5/61)
Properties	convex, face-transitive
Truncated dodecahedron (dual polyhedron)	Net

In geometry, the triakis icosahedron (or kisicosahedron^[1]) is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated dodecahedron.

Cartesian coordinates[]

Let ${\displaystyle \phi }$ be the golden ratio. The 12 points given by ${\displaystyle (0,\pm 1,\pm \phi )}$ and cyclic permutations of these coordinates are the vertices of a regular icosahedron. Its dual regular dodecahedron, whose edges intersect those of the icosahedron at right angles, has as vertices the points ${\displaystyle (\pm 1,\pm 1,\pm 1)}$ together with the points ${\displaystyle (\pm \phi ,\pm 1/\phi ,0)}$ and cyclic permutations of these coordinates. Multiplying all coordinates of this dodecahedron by a factor of ${\displaystyle (7\phi -1)/11\approx 0.938\,748\,901\,93}$ gives a slightly smaller dodecahedron. The 20 vertices of this dodecahedron, together with the vertices of the icosahedron, are the vertices of a triakis icosahedron centered at the origin. The length of its long edges equals ${\displaystyle 2}$. Its faces are isosceles triangles with one obtuse angle of ${\displaystyle \arccos(-3\phi /10)\approx 119.009\,350\,869\,29^{\circ }}$ and two acute ones of ${\displaystyle \arccos((\phi +7)/10)\approx 30.480\,324\,565\,36^{\circ }}$. The length ratio between the long and short edges of these triangles equals ${\displaystyle (\phi +7)/5\approx 1.723\,606\,797\,75}$.

Orthogonal projections[]

The triakis icosahedron has three symmetry positions, two on vertices, and one on a midedge: The Triakis icosahedron has five special orthogonal projections, centered on a vertex, on two types of edges, and two types of faces: hexagonal and pentagonal. The last two correspond to the A₂ and H₂ Coxeter planes.

Orthogonal projections of wireframe modes

Projective symmetry	[2]	[6]	[10]
Image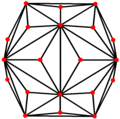
Dual image

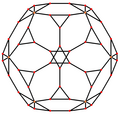
Kleetope[]

It can be seen as an icosahedron with triangular pyramids augmented to each face; that is, it is the Kleetope of the icosahedron. This interpretation is expressed in the name, triakis.

If the icosahedron is augmented by tetrahedral without removing the center icosahedron, one gets the net of an icosahedral pyramid.

Other triakis icosahedra[]

This interpretation can also apply to other similar nonconvex polyhedra with pyramids of different heights:

• First stellation of icosahedron, or Small triambic icosahedron, or sometimes called a Triakis icosahedron (among others)
• Great stellated dodecahedron (with very tall pyramids)
• Great dodecahedron (with inverted pyramids)

Stellations[]

The triakis icosahedron has numerous stellations, including this one.

Related polyhedra[]

Family of uniform icosahedral polyhedra
Symmetry: [5,3], (*532)							[5,3]+, (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Duals to uniform polyhedra
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

The triakis icosahedron is a part of a sequence of polyhedra and tilings, extending into the hyperbolic plane. These face-transitive figures have (*n32) reflectional symmetry.

*n32 symmetry mutation of truncated tilings: t{n,3} v
Symmetry *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paraco.	Noncompact hyperbolic
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Truncated figures
Symbol	t{2,3}	t{3,3}	t{4,3}	t{5,3}	t{6,3}	t{7,3}	t{8,3}	t{∞,3}	t{12i,3}	t{9i,3}	t{6i,3}
Triakis figures
Config.	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14	V3.16.16	V3.∞.∞

See also[]

• Kotzig's theorem, for which the triakis icosahedron gives an extreme case
• Triakis triangular tiling for other "triakis" polyhedral forms.
• Great triakis icosahedron

References[]

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
• Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
• Wenninger, Magnus (1983). Dual Models. Cambridge University Press. ISBN 978-0-521-54325-5. MR 0730208. (The thirteen semiregular convex polyhedra and their duals, Page 19, Triakisicosahedron)
• The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 [1] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 284, Triakis icosahedron )

External links[]

• Eric W. Weisstein, Triakis icosahedron (Catalan solid) at MathWorld.
• Triakis Icosahedron – Interactive Polyhedron Model