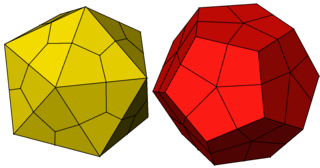
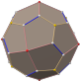
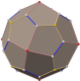
Deltoidal hexecontahedron
| Deltoidal hexecontahedron | |
|---|---|
 (Click here for rotating model) | |
| Type | Catalan |
| Conway notation | oD or deD |
| Coxeter diagram | |
| Face polygon |  kite |
| Faces | 60 |
| Edges | 120 |
| Vertices | 62 = 12 + 20 + 30 |
| Face configuration | V3.4.5.4 |
| Symmetry group | Ih, H3, [5,3], (*532) |
| Rotation group | I, [5,3]+, (532) |
| Dihedral angle | 154° 7′ 17′′ arccos(-19-8√5/41) |
| Properties | convex, face-transitive |
 rhombicosidodecahedron (dual polyhedron) |
 Net |

In geometry, a deltoidal hexecontahedron (also sometimes called a trapezoidal hexecontahedron, a strombic hexecontahedron, or a tetragonal hexacontahedron[1]) is a Catalan solid which is the dual polyhedron of the rhombicosidodecahedron, an Archimedean solid. It is one of six Catalan solids to not have a Hamiltonian path among its vertices.[2]
It is topologically identical to the nonconvex rhombic hexecontahedron.
Lengths and angles[]
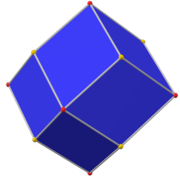
The 60 faces are deltoids or kites. The short and long edges of each kite are in the ratio 1:7 + √5/6 ≈ 1:1.539344663...
The angle between two short edges in a single face is arccos(-5-2√5/20)≈118.2686774705°. The opposite angle, between long edges, is arccos(-5+9√5/40)≈67.783011547435° . The other two angles of each face, between a short and a long edge each, are both equal to arccos(5-2√5/10)≈86.97415549104°.
The dihedral angle between any pair of adjacent faces is arccos(-19-8√5/41)≈154.12136312578°.
Topology[]
Topologically, the deltoidal hexecontahedron is identical to the nonconvex rhombic hexecontahedron. The deltoidal hexecontahedron can be derived from a dodecahedron (or icosahedron) by pushing the face centers, edge centers and vertices out to different radii from the body center. The radii are chosen so that the resulting shape has planar kite faces each such that vertices go to degree-3 corners, faces to degree-five corners, and edge centers to degree-four points.
Orthogonal projections[]
The deltoidal hexecontahedron has 3 symmetry positions located on the 3 types of vertices:
| Projective symmetry |
[2] | [2] | [2] | [2] | [6] | [10] |
|---|---|---|---|---|---|---|
| Image | 
|
|

|

|

|

|
| Dual image |

|

|
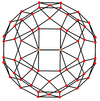
|

|
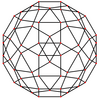
|

|
Variations[]

The deltoidal hexecontahedron can be constructed from either the regular icosahedron or regular dodecahedron by adding vertices mid-edge, and mid-face, and creating new edges from each edge center to the face centers. Conway polyhedron notation would give these as oI, and oD, ortho-icosahedron, and ortho-dodecahedron. These geometric variations exist as a continuum along one degree of freedom.
Related polyhedra and tilings[]
| Family of uniform icosahedral polyhedra | |||||||
|---|---|---|---|---|---|---|---|
| Symmetry: [5,3], (*532) | [5,3]+, (532) | ||||||

|

|

|

|

|

|

|

|
| {5,3} | t{5,3} | r{5,3} | t{3,5} | {3,5} | rr{5,3} | tr{5,3} | sr{5,3} |
| Duals to uniform polyhedra | |||||||

|

|

|

|

| |||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
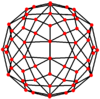
When projected onto a sphere (see right), it can be seen that the edges make up the edges of an icosahedron and dodecahedron arranged in their dual positions.
This tiling is topologically related as a part of sequence of deltoidal polyhedra with face figure (V3.4.n.4), and continues as tilings of the hyperbolic plane. These face-transitive figures have (*n32) reflectional symmetry.
| Symmetry *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | ||||
|---|---|---|---|---|---|---|---|---|
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] | |
| Figure Config. |
 V3.4.2.4 |
 V3.4.3.4 |
 V3.4.4.4 |
 V3.4.5.4 |
 V3.4.6.4 |
 V3.4.7.4 |
 V3.4.8.4 |
 V3.4.∞.4 |
See also[]
References[]
- ^ Conway, Symmetries of things, p.284-286
- ^ "Archimedean Dual Graph".
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 [1] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 286, tetragonal hexecontahedron)
- http://mathworld.wolfram.com/ArchimedeanDualGraph.html
External links[]
- Eric W. Weisstein, DeltoidalHexecontahedron and Hamiltonian path (Catalan solid) at MathWorld.
- Deltoidal Hexecontahedron (Trapezoidal Hexecontrahedron)—Interactive Polyhedron Model
- Example in real life—A ball almost 4 meters in diameter, from ripstop nylon, and inflated by the wind. It bounces around on the ground so that kids can play with it at kite festivals.
- Catalan solids
- Polyhedron stubs