Bipyramid

Set of dual-uniform n-gonal bipyramids
Example dual-uniform hexagonal bipyramid
Type	dual-uniform in the sense of dual-semiregular polyhedron
Coxeter diagram
Schläfli symbol	{ } + {n}[1]
Faces	2n congruent isosceles triangles
Edges	3n
Vertices	2 + n
Face configuration	V4.4.n
Symmetry group	Dnh, [n,2], (*n22), order 4n
Rotation group	Dn, [n,2]+, (n22), order 2n
Dual polyhedron	(convex) uniform n-gonal prism
Properties	convex, face-transitive, regular vertices[2]
Net	Example pentagonal bipyramid net (n = 5)

A bipyramid made with straws and elastics. (An extra axial straw is added which doesn't exist in the simple polyhedron.)

A (symmetric) n-gonal bipyramid or dipyramid is a polyhedron formed by joining an n-gonal pyramid and its mirror image base-to-base.^[3][4] An n-gonal bipyramid has 2n triangle faces, 3n edges, and 2 + n vertices.

The referenced n-gon in the name of a bipyramid is not a face but the internal polygon base, lying in the mirror plane that connects the two pyramid halves. (If it were a face, then each of its edges would connect three faces instead of two.)

"Regular", right bipyramids[]

A "regular" bipyramid has a regular polygon base. It is usually implied to be also a right bipyramid.

A right bipyramid has its two apices right above and right below the center or the centroid of its polygon base.

A "regular" right (symmetric) n-gonal bipyramid has Schläfli symbol { } + {n}.

A right (symmetric) bipyramid has Schläfli symbol { } + P, for polygon base P.

The "regular" right (thus face-transitive) n-gonal bipyramid with regular vertices^[2] is the dual of the n-gonal uniform (thus right) prism, and has congruent isosceles triangle faces.

A "regular" right (symmetric) n-gonal bipyramid can be projected on a sphere or globe as a "regular" right (symmetric) n-gonal spherical bipyramid: n equally spaced lines of longitude going from pole to pole, and an equator line bisecting them.

"Regular" right (symmetric) n-gonal bipyramids:

Bipyramid name	Digonal bipyramid	Triangular bipyramid (See: J12)	Square bipyramid (See: O)	Pentagonal bipyramid (See: J13)	Hexagonal bipyramid	Heptagonal bipyramid	Octagonal bipyramid	Enneagonal bipyramid	Decagonal bipyramid	...	Apeirogonal bipyramid
Polyhedron image										...
Spherical tiling image										Plane tiling image
Face config.	V2.4.4	V3.4.4	V4.4.4	V5.4.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4	...	V∞.4.4
Coxeter diagram										...

Equilateral triangle bipyramids[]

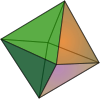
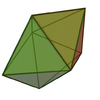
Only three kinds of bipyramids can have all edges of the same length (which implies that all faces are equilateral triangles, and thus the bipyramid is a deltahedron): the "regular" right (symmetric) triangular, tetragonal, and pentagonal bipyramids. The tetragonal or square bipyramid with same length edges, or regular octahedron, counts among the Platonic solids; the triangular and pentagonal bipyramids with same length edges count among the Johnson solids (J₁₂ and J₁₃).

Equilateral triangle bipyramids:

"Regular" right (symmetric) bipyramid name	Triangular bipyramid (J12)	Tetragonal bipyramid (Regular octahedron)	Pentagonal bipyramid (J13)
Bipyramid image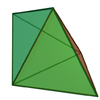

Kaleidoscopic symmetry[]

A "regular" right (symmetric) n-gonal bipyramid has dihedral symmetry group D_nh, of order 4n, except in the case of a regular octahedron, which has the larger octahedral symmetry group O_h, of order 48, which has three versions of D_4h as subgroups. The rotation group is D_n, of order 2n, except in the case of a regular octahedron, which has the larger rotation group O, of order 24, which has three versions of D₄ as subgroups.

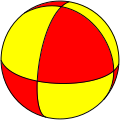
The 4n triangle faces of a "regular" right (symmetric) 2n-gonal bipyramid, projected as the 4n spherical triangle faces of a "regular" right (symmetric) 2n-gonal spherical bipyramid, represent the fundamental domains of dihedral symmetry in three dimensions: D_nh, [n,2], (*n22), order 4n. These domains can be shown as alternately colored spherical triangles:

• in a reflection plane through cocyclic edges, mirror image domains are in different colors (indirect isometry);
• about an n-fold rotation axis through opposite vertices, a domain and its image are in the same color (direct isometry).

An n-gonal (symmetric) bipyramid can be seen as the Kleetope of the "corresponding" n-gonal dihedron.

Fundamental domains of dihedral symmetry in three dimensions:

Dnh	D1h	D2h	D3h	D4h	D5h	D6h	...
Fundamental domains image							...

Volume[]

Volume of a (symmetric) bipyramid:

${\displaystyle V={\frac {2}{3}}Bh\,,}$

where B is the area of the base and h the height from the base plane to an apex.

This works for any shape of the base, and for any location of the apex, provided that h is measured as the perpendicular distance from the plane which contains the internal polygon base. Hence:

Volume of a (symmetric) bipyramid whose base is a regular n-sided polygon with side length s and whose height is h:

${\displaystyle V={\frac {n}{6}}hs^{2}\cot {\frac {\pi }{n}}\,.}$

Oblique bipyramids[]

Non-right bipyramids are called oblique bipyramids.

Concave bipyramids[]

A concave bipyramid has a concave polygon base.

Example concave (symmetric) tetragonal bipyramid (*)

(*) Its base has no obvious centroid; if its apices are not right above/below the gravity center of its base, it is not a right bipyramid. Anyway, it is a concave octahedron.

Asymmetric/inverted right bipyramids[]

An asymmetric right bipyramid joins two right pyramids with congruent bases but unequal heights, base-to-base.

An inverted right bipyramid joins two right pyramids with congruent bases but unequal heights, base-to-base, but on the same side of their common base.

The dual of an asymmetric or inverted right bipyramid is a frustum.

A "regular" asymmetric/inverted right n-gonal bipyramid has symmetry group C_nv, of order 2n.

Example "regular" asymmetric/inverted right hexagonal bipyramids:

Asymmetric	Inverted

Scalene triangle bipyramids[]

Example ditetragonal bipyramid

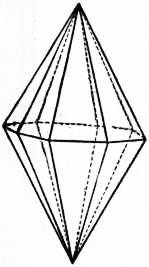
An "isotoxal" right (symmetric) di-n-gonal bipyramid is a right (symmetric) 2n-gonal bipyramid with an isotoxal flat polygon base: its 2n vertices around sides are coplanar, but alternate in two radii.

An "isotoxal" right (symmetric) di-n-gonal bipyramid has n two-fold rotation axes through vertices around sides, n reflection planes through vertices and apices, an n-fold rotation axis through apices, a reflection plane through base, and an n-fold rotation-reflection axis through apices,^[4] representing symmetry group D_nh, [n,2], (*22n), of order 4n. (The reflection in base plane corresponds to the 0° rotation-reflection. If n is even, there is a symmetry about the center, corresponding to the 180° rotation-reflection.)

All its faces are congruent scalene triangles, and it is isohedral. It can be seen as another type of right "symmetric" di-n-gonal scalenohedron.

Note: For at most two particular apex heights, triangle faces may be isosceles.^{[citation needed]}

Example:

• The "isotoxal" right (symmetric) "didigonal" (*) bipyramid with base vertices:

U = (1,0,0), U′ = (−1,0,0), V = (0,2,0), V′ = (0,−2,0),

and with apices:

A = (0,0,1), A′ = (0,0,−1),

has two different edge lengths:

UV = UV′ = U′V = U′V′ = √5,

AU = AU′ = A′U = A′U′ = √2,

AV = AV′ = A′V = A′V′ = √5;

thus all its triangle faces are isosceles.

• The "isotoxal" right (symmetric) "didigonal" (*) bipyramid with the same base vertices, but with apex height: 2, also has two different edge lengths: √5 and 2√2.

In crystallography, "isotoxal" right (symmetric) "didigonal" (*) (8-faced), ditrigonal (12-faced), ditetragonal (16-faced), and dihexagonal (24-faced) bipyramids exist.^[4][3]

Example rhombic bipyramids

(*) The smallest geometric di-n-gonal bipyramids have eight faces, and are topologically identical to the regular octahedron. In this case (2n = 2×2):
an "isotoxal" right (symmetric) "didigonal" bipyramid is called a rhombic bipyramid,^[4][3] although all its faces are scalene triangles, because its flat polygon base is a rhombus.

Scalenohedra[]

A "regular" right "symmetric" di-n-gonal scalenohedron can be made with a regular zigzag skew 2n-gon base, two symmetric apices right above and right below the base center, and triangle faces connecting each base edge to each apex.

It has two apices and 2n vertices around sides, 4n faces, and 6n edges; it is topologically identical to a 2n-gonal bipyramid, but its 2n vertices around sides alternate in two rings above and below the center.^[3]

Example ditrigonal scalenohedron

A "regular" right "symmetric" di-n-gonal scalenohedron has n two-fold rotation axes through mid-edges around sides, n reflection planes through vertices and apices, an n-fold rotation axis through apices, and an n-fold rotation-reflection axis through apices,^[4] representing symmetry group D_nv = D_nd, [2⁺,2n], (2*n), of order 4n. (If n is odd, there is a symmetry about the center, corresponding to the 180° rotation-reflection.)

All its faces are congruent scalene triangles, and it is isohedral. It can be seen as another type of right "symmetric" 2n-gonal bipyramid, with a regular zigzag skew polygon base.

Note: For at most two particular apex heights, triangle faces may be isoceles.

In crystallography, "regular" right "symmetric" "didigonal" (8-faced) and ditrigonal (12-faced) scalenohedra exist.^[4][3]

The smallest geometric scalenohedra have eight faces, and are topologically identical to the regular octahedron. In this case (2n = 2×2):
a "regular" right "symmetric" "didigonal" scalenohedron is called a tetragonal scalenohedron;^[4][3] its six vertices can be represented as (0,0,±1), (±1,0,z), (0,±1,−z), where z is a parameter between 0 and 1; at z = 0, it is a regular octahedron; at z = 1, it is a disphenoid with all merged coplanar faces (four congruent isosceles triangles); for z > 1, it becomes concave.

"Regular" right "symmetric" 8-faced scalenohedron geometric variations:

z = 0.1	z = 0.25	z = 0.5	z = 0.95	z = 1.5

Example disphenoids and 8-faced scalenohedron

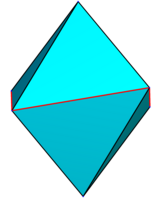
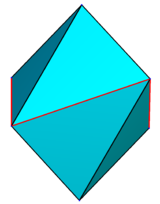
Note: If the 2n-gon base is both isotoxal in-out and zigzag skew, then not all triangle faces of the "isotoxal" right "symmetric" solid are congruent.

Example:

• The solid with isotoxal in-out zigzag skew 2×2-gon base vertices:

U = (1,0,1), U′ = (−1,0,1), V = (0,2,−1), V′ = (0,−2,−1),

and with "right" symmetric apices:

A = (0,0,3), A′ = (0,0,3),

has five different edge lengths:

UV = UV′ = U′V = U′V′ = 3,

AU = AU′ = √5,

AV = AV′ = 2√5,

A′U = A′U′ = √17,

A′V = A′V′ = 2√2;

thus not all its triangle faces are congruent.

"Regular" star bipyramids[]

A self-intersecting or star bipyramid has a star polygon base.

A "regular" right symmetric star bipyramid can be made with a regular star polygon base, two symmetric apices right above and right below the base center, and thus one-to-one symmetric triangle faces connecting each base edge to each apex.

A "regular" right symmetric star bipyramid has congruent isosceles triangle faces, and is isohedral.

Note: For at most one particular apex height, triangle faces may be equilateral.

A {p/q}-bipyramid has Coxeter diagram .

Example "regular" right symmetric star bipyramids:

Star polygon base	5/2-gon	7/2-gon	7/3-gon	8/3-gon	9/2-gon	9/4-gon
Star bipyramid image
Coxeter diagram

Example "regular" right symmetric star bipyramids:

Star polygon base	10/3-gon	11/2-gon	11/3-gon	11/4-gon	11/5-gon	12/5-gon
Star bipyramid image
Coxeter diagram

Scalene triangle star bipyramids[]

An "isotoxal" right symmetric 2p/q-gonal star bipyramid can be made with an isotoxal in-out star 2p/q-gon base, two symmetric apices right above and right below the base center, and thus one-to-one symmetric triangle faces connecting each base edge to each apex.

An "isotoxal" right symmetric 2p/q-gonal star bipyramid has congruent scalene triangle faces, and is isohedral. It can be seen as another type of 2p/q-gonal right "symmetric" star scalenohedron.

Note: For at most two particular apex heights, triangle faces may be isoceles.

Example "isotoxal" right symmetric star bipyramid:

Star polygon base	Isotoxal in-out 8/3-gon
Scalene triangle star bipyramid image

Star scalenohedra[]

A "regular" right "symmetric" 2p/q-gonal star scalenohedron can be made with a regular zigzag skew star 2p/q-gon base, two symmetric apices right above and right below the base center, and triangle faces connecting each base edge to each apex.

A "regular" right "symmetric" 2p/q-gonal star scalenohedron has congruent scalene triangle faces, and is isohedral. It can be seen as another type of right "symmetric" 2p/q-gonal star bipyramid, with a regular zigzag skew star polygon base.

Note: For at most two particular apex heights, triangle faces may be isosceles.

Example "regular" right "symmetric" star scalenohedron:

Star polygon base	Regular zigzag skew 8/3-gon
Star scalenohedron image

Note: If the star 2p/q-gon base is both isotoxal in-out and zigzag skew, then not all triangle faces of the "isotoxal" right "symmetric" star polyhedron are congruent.

Example "isotoxal" right "symmetric" star polyhedron:

Star polygon base	Isotoxal in-out zigzag skew 8/3-gon
Star polyhedron image

With base vertices:

U₀ = (1,0,1), U₁ = (0,1,1), U₂ = (−1,0,1), U₃ = (0,−1,1),

V₀ = (2,2,−1), V₁ = (−2,2,−1), V₂ = (−2,−2,−1), V₃ = (2,−2,−1),

and with apices:

A = (0,0,3), A′ = (0,0,−3),

it has four different edge lengths:

U₀V₁ = V₁U₃ = U₃V₀ = V₀U₂ = U₂V₃ = V₃U₁ = U₁V₂ = V₂U₀ = √17,

AU₀ = AU₁ = AU₂ = AU₃ = √5,

AV₀ = AV₁ = AV₂ = AV₃ = 2√6,

A′U₀ = A′U₁ = A′U₂ = A′U₃ = √17,

A′V₀ = A′V₁ = A′V₂ = A′V₃ = 2√3;

thus not all its triangle faces are congruent.

4-polytopes with bipyramidal cells[]

The dual of the rectification of each convex regular 4-polytopes is a cell-transitive 4-polytope with bipyramidal cells. In the following, the apex vertex of the bipyramid is A and an equator vertex is E. The distance between adjacent vertices on the equator EE = 1, the apex to equator edge is AE and the distance between the apices is AA. The bipyramid 4-polytope will have V_A vertices where the apices of N_A bipyramids meet. It will have V_E vertices where the type E vertices of N_E bipyramids meet. N_AE bipyramids meet along each type AE edge. N_EE bipyramids meet along each type EE edge. C_AE is the cosine of the dihedral angle along an AE edge. C_EE is the cosine of the dihedral angle along an EE edge. As cells must fit around an edge, N_AA cos⁻¹(C_AA) ≤ 2π, N_AE cos⁻¹(C_AE) ≤ 2π.

4-polytope properties									Bipyramid properties
Dual of	Coxeter diagram	Cells	VA	VE	NA	NE	NAE	NEE	Cell	Coxeter diagram	AA	AE**	CAE	CEE
Rectified 5-cell		10	5	5	4	6	3	3	Triangular bipyramid		${\textstyle {\frac {2}{3}}}$	0.667	${\textstyle -{\frac {1}{7}}}$	${\textstyle -{\frac {1}{7}}}$
Rectified tesseract		32	16	8	4	12	3	4	Triangular bipyramid		${\textstyle {\frac {\sqrt {2}}{3}}}$	0.624	${\textstyle -{\frac {2}{5}}}$	${\textstyle -{\frac {1}{5}}}$
Rectified 24-cell		96	24	24	8	12	4	3	Triangular bipyramid		${\textstyle {\frac {2{\sqrt {2}}}{3}}}$	0.745	${\textstyle {\frac {1}{11}}}$	${\textstyle -{\frac {5}{11}}}$
Rectified 120-cell		1200	600	120	4	30	3	5	Triangular bipyramid		${\textstyle {\frac {{\sqrt {5}}-1}{3}}}$	0.613	${\textstyle -{\frac {10+9{\sqrt {5}}}{61}}}$	${\textstyle -{\frac {7-12{\sqrt {5}}}{61}}}$
Rectified 16-cell		24*	8	16	6	6	3	3	Square bipyramid		${\textstyle {\sqrt {2}}}$	1	${\textstyle -{\frac {1}{3}}}$	${\textstyle -{\frac {1}{3}}}$
Rectified cubic honeycomb		∞	∞	∞	6	12	3	4	Square bipyramid		${\textstyle 1}$	0.866	${\textstyle -{\frac {1}{2}}}$	${\textstyle 0}$
Rectified 600-cell		720	120	600	12	6	3	3	Pentagonal bipyramid		${\textstyle {\frac {5+3{\sqrt {5}}}{5}}}$	1.447	${\textstyle -{\frac {11+4{\sqrt {5}}}{41}}}$	${\textstyle -{\frac {11+4{\sqrt {5}}}{41}}}$

* The rectified 16-cell is the regular 24-cell and vertices are all equivalent – octahedra are regular bipyramids.

** Given numerically due to more complex form.

Higher dimensions[]

In general, a bipyramid can be seen as an n-polytope constructed with a (n − 1)-polytope in a hyperplane with two points in opposite directions, equal distance perpendicular from the hyperplane. If the (n − 1)-polytope is a regular polytope, it will have identical pyramidal facets. An example is the 16-cell, which is an octahedral bipyramid, and more generally an n-orthoplex is an (n − 1)-orthoplex bipyramid.

A two-dimensional bipyramid is a rhombus.

See also[]

• Trapezohedron

References[]

Citations[]

General references[]

• Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. Chapter 4: Duals of the Archimedean polyhedra, prisma and antiprisms

External links[]

Wikimedia Commons has media related to Bipyramids.

• Weisstein, Eric W. "Dipyramid". MathWorld.
• Weisstein, Eric W. "Isohedron". MathWorld.
• The Uniform Polyhedra
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra
  • VRML models (George Hart) <3> <4> <5> <6> <7> <8> <9> <10>
    • Conway Notation for Polyhedra Try: "dPn", where n = 3, 4, 5, 6, ... example "dP4" is an octahedron.