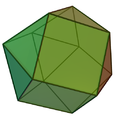
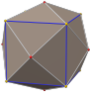
Cuboctahedron

Cuboctahedron
(Click here for rotating model)
Type	Archimedean solid Uniform polyhedron
Elements	F = 14, E = 24, V = 12 (χ = 2)
Faces by sides	8{3}+6{4}
Conway notation	aC aaT
Schläfli symbols	r{4,3} or ${\displaystyle {\begin{Bmatrix}4\\3\end{Bmatrix}}}$ rr{3,3} or ${\displaystyle r{\begin{Bmatrix}3\\3\end{Bmatrix}}}$
	t1{4,3} or t0,2{3,3}
Wythoff symbol	2 | 3 4 3 3 | 2
Coxeter diagram	or or
Symmetry group	Oh, B3, [4,3], (*432), order 48 Td, [3,3], (*332), order 24
Rotation group	O, [4,3]+, (432), order 24
Dihedral angle	125.26° arcsec(−√3)
References	U07, C19, W11
Properties	Semiregular convex quasiregular
Colored faces	3.4.3.4 (Vertex figure)
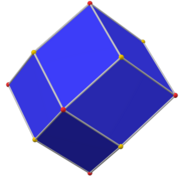
Rhombic dodecahedron (dual polyhedron)	Net

3D model of a cuboctahedron

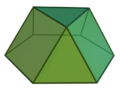
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it is a quasiregular polyhedron, i.e. an Archimedean solid that is not only vertex-transitive but also edge-transitive. It is radially equilateral.

Its dual polyhedron is the rhombic dodecahedron.

The cuboctahedron was probably known to Plato: Heron's Definitiones quotes Archimedes as saying that Plato knew of a solid made of 8 triangles and 6 squares.^[1]

Other names[]

• Heptaparallelohedron (Buckminster Fuller)
  • Fuller applied the name "Dymaxion" to this shape, used in an early version of the Dymaxion map. He also called it the "Vector Equilibrium" because of its radial equilateral symmetry (its center-to-vertex radius equals its edge length).^[2] He called a cuboctahedron consisting of rigid struts connected by flexible vertices a "jitterbug" (this shape can be progressively deformed into an icosahedron, octahedron, and tetrahedron by collapsing its square sides).
• With O_h symmetry, order 48, it is a rectified cube or rectified octahedron (Norman Johnson)
• With T_d symmetry, order 24, it is a cantellated tetrahedron or rhombitetratetrahedron.
• With D_3d symmetry, order 12, it is a triangular gyrobicupola.

Area and volume[]

The area A and the volume V of the cuboctahedron of edge length a are:

${\displaystyle {\begin{aligned}A&=\left(6+2{\sqrt {3}}\right)a^{2}&&\approx 9.464\,1016a^{2}\\V&={\tfrac {5}{3}}{\sqrt {2}}a^{3}&&\approx 2.357\,0226a^{3}.\end{aligned}}}$

Orthogonal projections[]

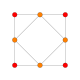
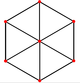
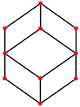
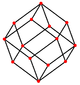
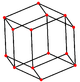
The cuboctahedron has four special orthogonal projections, centered on a vertex, an edge, and the two types of faces, triangular and square. The last two correspond to the B₂ and A₂ Coxeter planes. The skew projections show a square and hexagon passing through the center of the cuboctahedron.

Cuboctahedron (orthogonal projections)

Square Face	Triangular Face	Vertex	Edge	Skew
[4]	[6]	[2]	[2]
Rhombic dodecahedron (Dual polyhedron)

Spherical tiling[]

The cuboctahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.

orthographic projection	square-centered	triangle-centered	Vertex centered
	Stereographic projection

Cartesian coordinates[]

The Cartesian coordinates for the vertices of a cuboctahedron (of edge length √2) centered at the origin are:

(±1,±1,0)

(±1,0,±1)

(0,±1,±1)

An alternate set of coordinates can be made in 4-space, as 12 permutations of:

(0,1,1,2)

This construction exists as one of 16 orthant facets of the cantellated 16-cell.

Root vectors[]

The cuboctahedron's 12 vertices can represent the root vectors of the simple Lie group A₃. With the addition of 6 vertices of the octahedron, these vertices represent the 18 root vectors of the simple Lie group B₃.

Dissection[]

The cuboctahedron can be dissected into two triangular cupolas by a common hexagon passing through the center of the cuboctahedron. If these two triangular cupolas are twisted so triangles and squares line up, Johnson solid J₂₇, the triangular orthobicupola, is created.

The cuboctahedron can also be dissected into 6 square pyramids and 8 tetrahedra meeting at a central point. This dissection is expressed in the alternated cubic honeycomb where pairs of square pyramids are combined into octahedra.

Geometric relations[]

Progression between a tetrahedron, expanded into a cuboctahedron, and reverse expanded into the dual tetrahedron

Radial equilateral symmetry[]

Progressions between an octahedron, pseudoicosahedron, and cuboctahedron

In a cuboctahedron, the long radius (center to vertex) is the same as the edge length; thus its long diameter (vertex to opposite vertex) is 2 edge lengths. Its center is like the apical vertex of a pyramid: one edge length away from all the other vertices. (In the case of the cuboctahedron, the center is in fact the apex of 6 square and 8 triangular pyramids). This radial equilateral symmetry is a property of only a few uniform polytopes, including the two-dimensional hexagon, the three-dimensional cuboctahedron, and the four-dimensional 24-cell and 8-cell (tesseract). Radially equilateral polytopes are those which can be constructed, with their long radii, from equilateral triangles which meet at the center of the polytope, each contributing two radii and an edge. Therefore, all the interior elements which meet at the center of these polytopes have equilateral triangle inward faces, as in the dissection of the cuboctahedron into 6 square pyramids and 8 tetrahedra.

Each of these radially equilateral polytopes also occurs as cells of a characteristic space-filling tessellation: the tiling of regular hexagons, the rectified cubic honeycomb (of alternating cuboctahedra and octahedra), the 24-cell honeycomb and the tesseractic honeycomb, respectively. Each tessellation has a dual tessellation; the cell centers in a tessellation are cell vertices in its dual tessellation. The densest known regular sphere-packing in two, three and four dimensions uses the cell centers of one of these tessellations as sphere centers.

A cuboctahedron has octahedral symmetry. Its first stellation is the compound of a cube and its dual octahedron, with the vertices of the cuboctahedron located at the midpoints of the edges of either.

Constructions[]

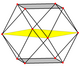
A cuboctahedron can be obtained by taking an equatorial cross section of a four-dimensional 24-cell or 16-cell. A hexagon can be obtained by taking an equatorial cross section of a cuboctahedron.

The cuboctahedron is a rectified cube and also a rectified octahedron.

It is also a cantellated tetrahedron. With this construction it is given the Wythoff symbol: 3 3 | 2.

A skew cantellation of the tetrahedron produces a solid with faces parallel to those of the cuboctahedron, namely eight triangles of two sizes, and six rectangles. While its edges are unequal, this solid remains vertex-uniform: the solid has the full tetrahedral symmetry group and its vertices are equivalent under that group.

The edges of a cuboctahedron form four regular hexagons. If the cuboctahedron is cut in the plane of one of these hexagons, each half is a triangular cupola, one of the Johnson solids; the cuboctahedron itself thus can also be called a triangular gyrobicupola, the simplest of a series (other than the gyrobifastigium or "digonal gyrobicupola"). If the halves are put back together with a twist, so that triangles meet triangles and squares meet squares, the result is another Johnson solid, the triangular orthobicupola, also called an anticuboctahedron.

Both triangular bicupolae are important in sphere packing. The distance from the solid's center to its vertices is equal to its edge length. Each central sphere can have up to twelve neighbors, and in a face-centered cubic lattice these take the positions of a cuboctahedron's vertices. In a hexagonal close-packed lattice they correspond to the corners of the triangular orthobicupola. In both cases the central sphere takes the position of the solid's center.

Cuboctahedra appear as cells in three of the convex uniform honeycombs and in nine of the convex uniform 4-polytopes.

The volume of the cuboctahedron is 5/6 of that of the enclosing cube and 5/8 of that of the enclosing octahedron.

Vertex arrangement[]

Because it is radially equilateral, the cuboctahedron's center can be treated as a 13th canonical apical vertex, one edge length distant from the 12 ordinary vertices, as the apex of a canonical pyramid is one edge length equidistant from its other vertices.

The cuboctahedron shares its edges and vertex arrangement with two nonconvex uniform polyhedra: the cubohemioctahedron (having the square faces in common) and the octahemioctahedron (having the triangular faces in common), both have four hexagons. It also serves as a cantellated tetrahedron, as being a rectified tetratetrahedron.

Cuboctahedron

its equator

Cubohemioctahedron

Octahemioctahedron

The cuboctahedron 2-covers the tetrahemihexahedron,^[3] which accordingly has the same abstract vertex figure (two triangles and two squares: 3.4.3.4) and half the vertices, edges, and faces. (The actual vertex figure of the tetrahemihexahedron is 3.4.3/2.4, with the a/2 factor due to the cross.)

Cuboctahedron

Tetrahemihexahedron

Related polyhedra[]

The cuboctahedron is one of a family of uniform polyhedra related to the cube and regular octahedron.

Uniform octahedral polyhedra
Symmetry: [4,3], (*432)							[4,3]+ (432)	[1+,4,3] = [3,3] (*332)		[3+,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{31,1}	t{3,4} t{31,1}	{3,4} {31,1}	rr{4,3} s2{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	s{3,4} s{31,1}
		=	=	=				= or	= or	=
Duals to uniform polyhedra
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V33	V3.62	V35

The cuboctahedron also has tetrahedral symmetry with two colors of triangles.

Family of uniform tetrahedral polyhedra
Symmetry: [3,3], (*332)							[3,3]+, (332)
{3,3}	t{3,3}	r{3,3}	t{3,3}	{3,3}	rr{3,3}	tr{3,3}	sr{3,3}
Duals to uniform polyhedra
V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

Related quasiregular polyhedra and tilings[]

The cuboctahedron exists in a sequence of symmetries of quasiregular polyhedra and tilings with vertex configurations (3.n)², progressing from tilings of the sphere to the Euclidean plane and into the hyperbolic plane. With orbifold notation symmetry of *n32 all of these tilings are wythoff construction within a fundamental domain of symmetry, with generator points at the right angle corner of the domain.^[4][5]

*n32 orbifold symmetries of quasiregular tilings: (3.n)2
Construction	Spherical			Euclidean	Hyperbolic
	*332	*432	*532	*632	*732	*832...	*∞32
Quasiregular figures
Vertex	(3.3)2	(3.4)2	(3.5)2	(3.6)2	(3.7)2	(3.8)2	(3.∞)2

*n42 symmetry mutations of quasiregular tilings: (4.n)2 v
Symmetry *4n2 [n,4]	Spherical	Euclidean	Compact hyperbolic				Paracompact	Noncompact
	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]	[ni,4]
Figures
Config.	(4.3)2	(4.4)2	(4.5)2	(4.6)2	(4.7)2	(4.8)2	(4.∞)2	(4.ni)2

This polyhedron is topologically related as a part of sequence of cantellated polyhedra with vertex figure (3.4.n.4), and continues as tilings of the hyperbolic plane. These vertex-transitive figures have (*n32) reflectional symmetry.

*n32 symmetry mutation of expanded tilings: 3.4.n.4
Symmetry *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paracomp.
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Figure
Config.	3.4.2.4	3.4.3.4	3.4.4.4	3.4.5.4	3.4.6.4	3.4.7.4	3.4.8.4	3.4.∞.4

Related polytopes[]

Orthogonal projections of 24-cell

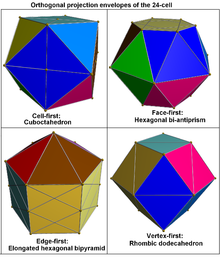
The cuboctahedron can be decomposed into a regular octahedron and eight irregular but equal octahedra in the shape of the convex hull of a cube with two opposite vertices removed. This decomposition of the cuboctahedron corresponds with the cell-first parallel projection of the 24-cell into three dimensions. Under this projection, the cuboctahedron forms the projection envelope, which can be decomposed into six square faces, a regular octahedron, and eight irregular octahedra. These elements correspond with the images of six of the octahedral cells in the 24-cell, the nearest and farthest cells from the 4D viewpoint, and the remaining eight pairs of cells, respectively.

Cultural occurrences[]

Two cuboctahedra on a chimney in Israel.

• In the Star Trek episode "By Any Other Name", aliens seize the Enterprise by transforming crew members into inanimate cuboctahedra.
• The "Geo Twister" fidget toy is a flexible cuboctahedron.
• The Coriolis space stations in the computer game series Elite are cuboctahedron-shaped.
• Vesak Kuudu, traditional lanterns made in Sri Lanka annually to celebrate Vesak Poya day, are usually cuboctahedral.
• "Moonsnakes" from Super Mario Odyssey.^[6]
• InfluxData, the company behind the InfluxDB time series database, uses the cuboctahedron in its logo.

Cuboctahedral graph[]

Cuboctahedral graph
4-fold symmetry
Vertices	12
Edges	24
Automorphisms	48
Properties	Quartic Hamiltonian regular locally linear
Table of graphs and parameters

In the mathematical field of graph theory, a cuboctahedral graph is the graph of vertices and edges of the cuboctahedron, one of the Archimedean solids. It can also be constructed as the line graph of the cube. It has 12 vertices and 24 edges, is locally linear, and is a quartic Archimedean graph.^[7]

orthogonal projection

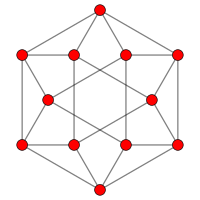6-fold symmetry

See also[]

• Icosidodecahedron
• Pseudocuboctahedron
• Rhombicuboctahedron
• Truncated cuboctahedron
• Tetradecahedron

References[]

Further reading[]

External links[]

• The Uniform Polyhedra
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra
• Eric W. Weisstein, Cuboctahedron (Archimedean solid) at MathWorld.
• The Cuboctahedron on Hexnet a website devoted to hexagon mathematics.
• Klitzing, Richard. "3D convex uniform polyhedra o3x4o - co".
• Editable printable net of a Cuboctahedron with interactive 3D view