Octagonal bipyramid

Octagonal bipyramid
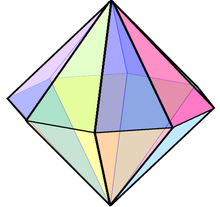Type	bipyramid
Faces	16 triangles
Edges	24
Vertices	10
Schläfli symbol	{ } + {8}
Coxeter diagram
Symmetry group	D8h, [8,2], (*228), order 32
Rotation group	D8, [8,2]+, (228), order 16
Dual polyhedron	octagonal prism
Face configuration	V4.4.8
Properties	convex, face-transitive

The octagonal bipyramid is one of the infinite set of bipyramids, dual to the infinite prisms. If an octagonal bipyramid is to be face-transitive, all faces must be isosceles triangles. 16-sided dice are often octagonal bipyramids.

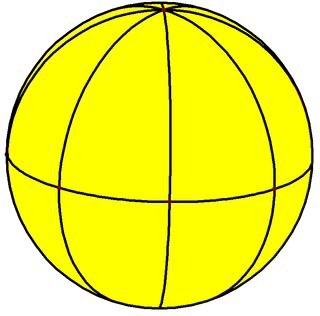
Images[]

It can be drawn as a tiling on a sphere which also represents the fundamental domains of [4,2], *422 symmetry:

Related polyhedra[]

"Regular" right (symmetric) n-gonal bipyramids:

Bipyramid name	Digonal bipyramid	Triangular bipyramid (See: J12)	Square bipyramid (See: O)	Pentagonal bipyramid (See: J13)	Hexagonal bipyramid	Heptagonal bipyramid	Octagonal bipyramid	Enneagonal bipyramid	Decagonal bipyramid	...	Apeirogonal bipyramid
Polyhedron image										...
Spherical tiling image										Plane tiling image
Face config.	V2.4.4	V3.4.4	V4.4.4	V5.4.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4	...	V∞.4.4
Coxeter diagram										...

*n42 symmetry mutation of omnitruncated tilings: 4.8.2n v
Symmetry *n42 [n,4]	Spherical		Euclidean	Compact hyperbolic				Paracomp.
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Omnitruncated figure	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	4.8.14	4.8.16	4.8.∞
Omnitruncated duals	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.∞

External links[]

• Weisstein, Eric W. "Dipyramid". MathWorld.
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra
  • VRML models <8>
  • Conway Notation for Polyhedra Try: dP8

This polyhedron-related article is a stub. You can help Wikipedia by .

• v
• t