Bilinski dodecahedron

From Wikipedia, the free encyclopedia
Bilinski dodecahedron (gray).png
(Animation)
Bilinski dodecahedron, ortho z.png
Bilinski dodecahedron, ortho y.png Bilinski dodecahedron, ortho x.png

(Dimensioning)

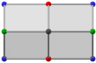
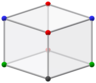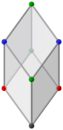Bilinski dodecahedron, ortho obtuse.png Bilinski dodecahedron, ortho acute.png
Orthogonal projections parallel to
2 opposite edges, each with:
black & red vertices / black & green vertices.
Also orthogonal projections of golden rhombohedra
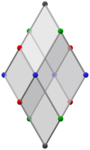Bilinski dodecahedron, ortho matrix.png Bilinski dodecahedron, ortho slanted.png
Orthogonal projections parallel to:
4 faces, each with all 4 kinds of vertices /
2 edges, each with black & blue vertices
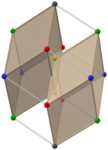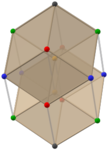Golden rhombohedra in Bilinski dodecahedron, 0 (acute).png Golden rhombohedra in Bilinski dodecahedron, 1 (obtuse).png
Pairs of golden rhombohedra
(Animations)

In geometry, the Bilinski dodecahedron is a convex polyhedron with twelve congruent golden rhombic faces. It has the same topology but different geometry from the face-transitive rhombic dodecahedron. It is a zonohedron.

History[]

This shape appears in a 1752 book by John Lodge Cowley, labeled as the dodecarhombus.[1][2] It is named after Stanko Bilinski, who rediscovered it in 1960.[3] Bilinski himself called it the rhombic dodecahedron of the second kind.[4] Bilinski's discovery corrected a 75-year-old omission in Evgraf Fedorov's classification of convex polyhedra with congruent rhombic faces.[5]

Properties[]

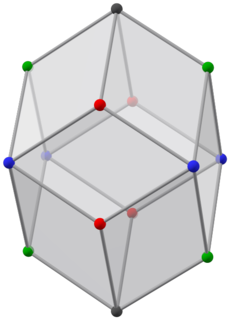
degree color coordinates
3 red (0, ±1, ±1) Right-handed coordinate system (y to back).png
green (±φ, 0, ±φ)
4 blue (±φ, ±1, 0)
black (0, 0, ±φ2)

Like its Catalan twin, the Bilinski dodecahedron has eight vertices of degree 3 and six of degree 4. But due to its different symmetry, it has four different kinds of vertices: the two on the "vertical" axis, and four on each axial plane (four vertices in all on the "horizontal" axial plane, six vertices in all on each of the two "vertical" axial planes).

Its faces are twelve congruent golden rhombi of three different kinds: two with alternating blue and red vertices (front and back), two with alternating blue and green vertices (left and right), and eight with all four kinds of vertices.

The symmetry group of this solid is the same as that of a rectangular cuboid: D2h. It is a subgroup of octahedral symmetry, and has eight elements: three axis of 2-fold symmetry, three symmetry planes (which are also the axial planes of this solid), and a centre of symmetry (since 2 is even).

It is a parallelohedron, and thus also a space-filling polyhedron.

Relation to rhombic dodecahedron[]

In a 1962 paper,[6] H. S. M. Coxeter claimed that the Bilinski dodecahedron could be obtained by an affine transformation from the rhombic dodecahedron, but this is false. For, in the Bilinski dodecahedron, the long body diagonal is parallel to the short diagonals of two faces, and to the long diagonals of two other faces. In the rhombic dodecahedron, the corresponding body diagonal is parallel to four short face diagonals, and in any affine transformation of the rhombic dodecahedron this body diagonal would remain parallel to four equal-length face diagonals. Another difference between the two dodecahedra is that, in the rhombic dodecahedron, all the body diagonals connecting opposite degree-4 vertices are parallel to face diagonals, while in the Bilinski dodecahedron the shorter body diagonals of this type have no parallel face diagonals.[5]

Related zonohedra[]

As a zonohedron, a Bilinski dodecahedron can be seen with 4 sets of 6 parallel edges. Contracting any set of 6 parallel edges to 0 length produces a golden rhombohedron.

The Bilinski dodecahedron can be formed from the rhombic triacontahedron (another zonohedron, with thirty congruent golden rhombic faces) by removing or collapsing two zones or belts of ten and eight golden rhombic faces with parallel edges. Removing only one zone of ten faces produces the rhombic icosahedron. Removing three zones of ten, eight, and six faces produces a golden rhombohedron.[4][5] Hence, removing a zone of six faces from the Bilinski dodecahedron produces a golden rhombohedron. The Bilinski dodecahedron can be dissected into four golden rhombohedra, two of each type.[7]

The vertices of these zonohedra can be computed by linear combinations of 3 to 6 vectors. A belt mn means a belt representing n directional vectors, and containing (at most) m coparallel congruent edges. The Bilinski dodecahedron has 4 belts of 6 coparallel edges.

These zonohedra are projection envelopes of the hypercubes, with n-dimensional projection basis, with golden ratio, φ. The specific basis for n=6 is:

x = (1, φ, 0, -1, φ, 0)
y = (φ, 0, 1, φ, 0, -1)
z = (0, 1, φ, 0, -1, φ)

For n=5 the basis is the same with the 6th column removed. For n=4 the 5th and 6th columns are removed.

Zonohedra with golden rhombic faces
Solid name Triacontahedron Icosahedron Dodecahedron Hexahedron Rhombus
Full
symmetry 		Ih
Order 120 		D5d
Order 20 		D2h
Order 8 		D3d
Order 12 		Dih2
Order 4
(2(n-1))n Belts 106 85 64 43 22
n(n-1) Faces 30 20
(−10) 		12
(−8) 		6
(−6) 		2
(−4)
2n(n-1) Edges 60 40
(−20) 		24
(−16) 		12
(−12) 		4
(−8)
n(n-1)+2 Vertices 32 22
(−10) 		14
(−8) 		8
(−6) 		4
(−4)
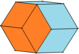
Solid image Rhombic triacontahedron middle colored.png Rhombic icosahedron colored as expanded Bilinski dodecahedron.png Bilinski dodecahedron as expanded golden rhombohedron.png Acute golden rhombohedron.pngFlat golden rhombohedron.png GoldenRhombus.svg
Parallel edges image Rhombic tricontahedron 6x10 parallels.png Rhombic icosahedron 5-color-paralleledges.png Bilinski dodecahedron parallelohedron.png
Dissection 10Acute golden rhombohedron.png + 10Flat golden rhombohedron.png 5Acute golden rhombohedron.png + 5Flat golden rhombohedron.png 2Acute golden rhombohedron.png + 2Flat golden rhombohedron.png
Projective
polytope		 6-cube 5-cube 4-cube 3-cube 2-cube
Projective
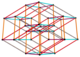
n-cube image 		6Cube-QuasiCrystal.png 5-cube-Phi-projection.png 4-cube-Phi-projection.png

References[]

  1. ^ Hart, George W. (2000), "A color-matching dissection of the rhombic enneacontahedron", Symmetry: Culture and Science, 11 (1–4): 183–199, MR 2001417.
  2. ^ Cowley, John Lodge (1752), Geometry Made Easy; Or, a New and Methodical Explanation of the Elements of Geometry, London, Plate 5, Fig. 16. As cited by Hart (2000).
  3. ^ Bilinski, S. (1960), "Über die Rhombenisoeder", Glasnik Mat. Fiz. Astr., 15: 251–263, Zbl 0099.15506.
  4. ^ a b Cromwell, Peter R. (1997), Polyhedra: One of the most charming chapters of geometry, Cambridge: Cambridge University Press, p. 156, ISBN 0-521-55432-2, MR 1458063.
  5. ^ a b c Grünbaum, Branko (2010), "The Bilinski dodecahedron and assorted parallelohedra, zonohedra, monohedra, isozonohedra, and otherhedra", The Mathematical Intelligencer, 32 (4): 5–15, doi:10.1007/s00283-010-9138-7, hdl:1773/15593, MR 2747698.
  6. ^ Coxeter, H. S. M. (1962), "The classification of zonohedra by means of projective diagrams", Journal de Mathématiques Pures et Appliquées, 41: 137–156, MR 0141004. Reprinted in Coxeter, H. S. M. (1968), Twelve geometric essays, Carbondale, Ill.: Southern Illinois University Press, MR 0310745 (The Beauty of Geometry. Twelve Essays, Dover, 1999, MR1717154).
  7. ^ "Golden Rhombohedra", CutOutFoldUp, retrieved 2016-05-26

External links[]

Retrieved from ""