Douady rabbit

The Douady rabbit is any of various particular filled Julia sets associated with the parameter near the center period 3 buds of Mandelbrot set for complex quadratic map.

• 

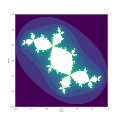
  colors show iterations

• 

  Gray levels indicate the speed of convergence to infinity or to the attractive cycle

• 

  boundaries of level sets

• 

  fat rabbit

• 

  with spine

• 

  external rays landing on fixed point ${\displaystyle \alpha _{c}\,}$.

• 

  Perturbated Rabbit ^[1]

• 

  Perturbated rabbit zoom

Name[]

Douady's rabbit or the Douady rabbit is named for the French mathematician Adrien Douady.^[2]

The fat rabbit or chubby rabbit has c at the root of 1/3-limb of the Mandelbrot set. It has a parabolic fixed point with 3 petals.^[3]

Forms of the complex quadratic map[]

There are two common forms for the complex quadratic map ${\displaystyle {\mathcal {M}}}$. The first, also called the complex logistic map, is written as

${\displaystyle z_{n+1}={\mathcal {M}}z_{n}=\gamma z_{n}\left(1-z_{n}\right),}$

where ${\displaystyle z}$ is a complex variable and ${\displaystyle \gamma }$ is a complex parameter. The second common form is

${\displaystyle w_{n+1}={\mathcal {M}}w_{n}=w_{n}^{2}-\mu .}$

Here ${\displaystyle w}$ is a complex variable and ${\displaystyle \mu }$ is a complex parameter. The variables ${\displaystyle z}$ and ${\displaystyle w}$ are related by the equation

${\displaystyle z=-{\frac {w}{\gamma }}+{\frac {1}{2}},}$

and the parameters ${\displaystyle \gamma }$ and ${\displaystyle \mu }$ are related by the equations

${\displaystyle \mu =\left({\frac {\gamma -1}{2}}\right)^{2}-{\frac {1}{4}}\quad ,\quad \gamma =1\pm {\sqrt {1+4\mu }}.}$

Note that ${\displaystyle \mu }$ is invariant under the substitution ${\displaystyle \gamma \to 2-\gamma }$.

Mandelbrot and filled Julia sets[]

There are two planes associated with ${\displaystyle {\mathcal {M}}}$. One of these, the ${\displaystyle z}$ (or ${\displaystyle w}$) plane, will be called the mapping plane, since ${\displaystyle {\mathcal {M}}}$ sends this plane into itself. The other, the ${\displaystyle \gamma }$ (or ${\displaystyle \mu }$) plane, will be called the control plane.

The nature of what happens in the mapping plane under repeated application of ${\displaystyle {\mathcal {M}}}$ depends on where ${\displaystyle \gamma }$ (or ${\displaystyle \mu }$) is in the control plane. The filled Julia set consists of all points in the mapping plane whose images remain bounded under indefinitely repeated applications of ${\displaystyle {\mathcal {M}}}$. The Mandelbrot set consists of those points in the control plane such that the associated filled Julia set in the mapping plane is connected.

Figure 1 shows the Mandelbrot set when ${\displaystyle \gamma }$ is the control parameter, and Figure 2 shows the Mandelbrot set when ${\displaystyle \mu }$ is the control parameter. Since ${\displaystyle z}$ and ${\displaystyle w}$ are affine transformations of one another (a linear transformation plus a translation), the filled Julia sets look much the same in either the ${\displaystyle z}$ or ${\displaystyle w}$ planes.

Figure 1: The Mandelbrot set in the ${\displaystyle \gamma }$ plane.

Figure 2: The Mandelbrot set in the ${\displaystyle \mu }$ plane.

The Douady rabbit[]

^{[clarification needed]}

Douady rabbit in an exponential family

Lamination of rabbit Julia set

Quaternion julia set with parameters c = −0,123 + 0.745i and with a cross-section in the XY plane. The "Douady Rabbit" julia set is visible in the cross section

Representation of the dynamics inside the rabbit.

The Douady rabbit is most easily described in terms of the Mandelbrot set as shown in Figure 1 (above). In this figure, the Mandelbrot set, at least when viewed from a distance, appears as two back-to-back unit discs with sprouts. Consider the sprouts at the one- and five-o'clock positions on the right disk or the sprouts at the seven- and eleven-o'clock positions on the left disk. When ${\displaystyle \gamma }$ is within one of these four sprouts, the associated filled Julia set in the mapping plane is a Douady rabbit. For these values of ${\displaystyle \gamma }$, it can be shown that ${\displaystyle {\mathcal {M}}}$ has ${\displaystyle z=0}$ and one other point as unstable (repelling) fixed points, and ${\displaystyle z=\infty }$ as an attracting fixed point. Moreover, the map ${\displaystyle {\mathcal {M}}^{3}}$ has three attracting fixed points. Douady's rabbit consists of the three attracting fixed points ${\displaystyle z_{1}}$, ${\displaystyle z_{2}}$, and ${\displaystyle z_{3}}$ and their basins of attraction.

For example, Figure 3 shows Douady's rabbit in the ${\displaystyle z}$ plane when ${\displaystyle \gamma =\gamma _{D}=2.55268-0.959456i}$, a point in the five-o'clock sprout of the right disk. For this value of ${\displaystyle \gamma }$, the map ${\displaystyle {\mathcal {M}}}$ has the repelling fixed points ${\displaystyle z=0}$ and ${\displaystyle z=.656747-.129015i}$. The three attracting fixed points of ${\displaystyle {\mathcal {M}}^{3}}$ (also called period-three fixed points) have the locations

${\displaystyle z^{1}=0.499997032420304-(1.221880225696050\times 10^{-6})i{\;}{\;}{\mathrm {(red)} },}$

${\displaystyle z^{2}=0.638169999974373-(0.239864000011495)i{\;}{\;}{\mathrm {(green)} },}$

${\displaystyle z^{3}=0.799901291393262-(0.107547238170383)i{\;}{\;}{\mathrm {(yellow)} }.}$

The red, green, and yellow points lie in the basins ${\displaystyle B(z^{1})}$, ${\displaystyle B(z^{2})}$, and ${\displaystyle B(z^{3})}$ of ${\displaystyle {\mathcal {M}}^{3}}$, respectively. The white points lie in the basin ${\displaystyle B(\infty )}$ of ${\displaystyle {\mathcal {M}}}$.

The action of ${\displaystyle {\mathcal {M}}}$ on these fixed points is given by the relations

${\displaystyle {\mathcal {M}}z^{1}=z^{2},}$

${\displaystyle {\mathcal {M}}z^{2}=z^{3},}$

${\displaystyle {\mathcal {M}}z^{3}=z^{1}.}$

Corresponding to these relations there are the results

${\displaystyle {\mathcal {M}}B(z^{1})=B(z^{2}){\;}{\mathrm {or} }{\;}{\mathcal {M}}{\;}{\mathrm {red} }\subseteq {\mathrm {green} },}$

${\displaystyle {\mathcal {M}}B(z^{2})=B(z^{3}){\;}{\mathrm {or} }{\;}{\mathcal {M}}{\;}{\mathrm {green} }\subseteq {\mathrm {yellow} },}$

${\displaystyle {\mathcal {M}}B(z^{3})=B(z^{1}){\;}{\mathrm {or} }{\;}{\mathcal {M}}{\;}{\mathrm {yellow} }\subseteq {\mathrm {red} }.}$

Note the marvelous fractal structure at the basin boundaries.

Figure 3: Douady's rabbit for ${\displaystyle \gamma =2.55268-0.959456i}$ or ${\displaystyle \mu =0.122565-0.744864i}$.

As a second example, Figure 4 shows a Douady rabbit when ${\displaystyle \gamma =2-\gamma _{D}=-.55268+.959456i}$, a point in the eleven-o'clock sprout on the left disk. (As noted earlier, ${\displaystyle \mu }$ is invariant under this transformation.) The rabbit now sits more symmetrically on the page. The period-three fixed points are located at

${\displaystyle z^{1}=0.500003730675024+(6.968273875812428\times 10^{-6})i{\;}{\;}({\mathrm {red} }),}$

${\displaystyle z^{2}=-0.138169999969259+(0.239864000061970)i{\;}{\;}({\mathrm {green} }),}$

${\displaystyle z^{3}=-0.238618870661709-(0.264884797354373)i{\;}{\;}({\mathrm {yellow} }),}$

The repelling fixed points of ${\displaystyle {\mathcal {M}}}$ itself are located at ${\displaystyle z=0}$ and ${\displaystyle z=1.450795+0.7825835i}$. The three major lobes on the left, which contain the period-three fixed points ${\displaystyle z^{1}}$,${\displaystyle z^{2}}$, and ${\displaystyle z^{3}}$, meet at the fixed point ${\displaystyle z=0}$, and their counterparts on the right meet at the point ${\displaystyle z=1}$. It can be shown that the effect of ${\displaystyle {\mathcal {M}}}$ on points near the origin consists of a counterclockwise rotation about the origin of ${\displaystyle \arg(\gamma )}$, or very nearly ${\displaystyle 120^{\circ }}$, followed by scaling (dilation) by a factor of ${\displaystyle |\gamma |=1.1072538}$.

Figure 4: Douady's rabbit for ${\displaystyle \gamma =-0.55268+0.959456i}$ or ${\displaystyle \mu =0.122565-0.744864i}$.

See also[]

• Dragon curve
• Herman ring
• Siegel disc
• ^[4][why?]

References[]

External links[]

• Weisstein, Eric W. "Douady Rabbit Fractal". MathWorld.
• Dragt, A. "Lie Methods for Nonlinear Dynamics with Applications to Accelerator Physics".

This article incorporates material from Douady Rabbit on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.