Lifting property

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help by introducing citations to additional sources. Find sources:  –  ·  ·  · scholar · JSTOR (April 2017)

In mathematics, in particular in category theory, the lifting property is a property of a pair of morphisms in a category. It is used in homotopy theory within algebraic topology to define properties of morphisms starting from an explicitly given class of morphisms. It appears in a prominent way in the theory of model categories, an axiomatic framework for homotopy theory introduced by Daniel Quillen. It is also used in the definition of a factorization system, and of a weak factorization system, notions related to but less restrictive than the notion of a model category. Several elementary notions may also be expressed using the lifting property starting from a list of (counter)examples.

Formal definition[]

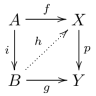
A morphism i in a category has the left lifting property with respect to a morphism p, and p also has the right lifting property with respect to i, sometimes denoted ${\displaystyle i\perp p}$ or ${\displaystyle i\downarrow p}$, iff the following implication holds for each morphism f and g in the category:

• if the outer square of the following diagram commutes, then there exists h completing the diagram, i.e. for each ${\displaystyle f:A\to X}$ and ${\displaystyle g:B\to Y}$ such that ${\displaystyle p\circ f=g\circ i}$ there exists ${\displaystyle h:B\to X}$ such that ${\displaystyle h\circ i=f}$ and ${\displaystyle p\circ h=g}$.

This is sometimes also known as the morphism i being orthogonal to the morphism p; however, this can also refer to the stronger property that whenever f and g are as above, the diagonal morphism h exists and is also required to be unique.

For a class C of morphisms in a category, its left orthogonal ${\displaystyle C^{\perp \ell }}$ or ${\displaystyle C^{\perp }}$ with respect to the lifting property, respectively its right orthogonal ${\displaystyle C^{\perp r}}$ or ${\displaystyle {}^{\perp }C}$, is the class of all morphisms which have the left, respectively right, lifting property with respect to each morphism in the class C. In notation,

${\displaystyle {\begin{aligned}C^{\perp \ell }&:=\{i\mid \forall p\in C,i\perp p\}\\C^{\perp r}&:=\{p\mid \forall i\in C,i\perp p\}\end{aligned}}}$

Taking the orthogonal of a class C is a simple way to define a class of morphisms excluding non-isomorphisms from C, in a way which is useful in a diagram chasing computation.

Thus, in the category Set of sets, the right orthogonal ${\displaystyle \{\emptyset \to \{*\}\}^{\perp r}}$ of the simplest non-surjection ${\displaystyle \emptyset \to \{*\},}$ is the class of surjections. The left and right orthogonals of ${\displaystyle \{x_{1},x_{2}\}\to \{*\},}$ the simplest non-injection, are both precisely the class of injections,

${\displaystyle \{\{x_{1},x_{2}\}\to \{*\}\}^{\perp \ell }=\{\{x_{1},x_{2}\}\to \{*\}\}^{\perp r}=\{f\mid f{\text{ is an injection }}\}.}$

It is clear that ${\displaystyle C^{\perp \ell r}\supset C}$ and ${\displaystyle C^{\perp r\ell }\supset C}$. The class ${\displaystyle C^{\perp r}}$ is always closed under retracts, pullbacks, (small) products (whenever they exist in the category) and composition of morphisms, and contains all isomorphisms of C. Meanwhile, ${\displaystyle C^{\perp \ell }}$ is closed under retracts, pushouts, (small) coproducts and transfinite composition (filtered colimits) of morphisms (whenever they exist in the category), and also contains all isomorphisms.

Examples[]

A number of notions can be defined by passing to the left or right orthogonal several times starting from a list of explicit examples, i.e. as ${\displaystyle C^{\perp \ell },C^{\perp r},C^{\perp \ell r},C^{\perp \ell \ell }}$, where ${\displaystyle C}$ is a class consisting of several explicitly given morphisms. A useful intuition is to think that the property of left-lifting against a class C is a kind of negation of the property of being in C, and that right-lifting is also a kind of negation. Hence the classes obtained from C by taking orthogonals an odd number of times, such as ${\displaystyle C^{\perp \ell },C^{\perp r},C^{\perp \ell r\ell },C^{\perp \ell \ell \ell }}$ etc., represent various kinds of negation of C, so ${\displaystyle C^{\perp \ell },C^{\perp r},C^{\perp \ell r\ell },C^{\perp \ell \ell \ell }}$ each consists of morphisms which are far from having property ${\displaystyle C}$.

Examples of lifting properties in algebraic topology[]

A map ${\displaystyle f:U\to B}$ has the path lifting property iff ${\displaystyle \{0\}\to [0,1]\perp f}$ where ${\displaystyle \{0\}\to [0,1]}$ is the inclusion of one end point of the closed interval into the interval ${\displaystyle [0,1]}$.

A map ${\displaystyle f:U\to B}$ has the homotopy lifting property iff ${\displaystyle X\to X\times [0,1]\perp f}$ where ${\displaystyle X\to X\times [0,1]}$ is the map ${\displaystyle x\mapsto (x,0)}$.

Examples of lifting properties coming from model categories[]

Fibrations and cofibrations.

• Let Top be the category of topological spaces, and let ${\displaystyle C_{0}}$ be the class of maps ${\displaystyle S^{n}\to D^{n+1}}$, embeddings of the boundary ${\displaystyle S^{n}=\partial D^{n+1}}$ of a ball into the ball ${\displaystyle D^{n+1}}$. Let ${\displaystyle WC_{0}}$ be the class of maps embedding the upper semi-sphere into the disk. ${\displaystyle WC_{0}^{\perp \ell },WC_{0}^{\perp \ell r},C_{0}^{\perp \ell },C_{0}^{\perp \ell r}}$ are the classes of fibrations, acyclic cofibrations, acyclic fibrations, and cofibrations.^[1]

• Let sSet be the category of simplicial sets. Let ${\displaystyle C_{0}}$ be the class of boundary inclusions ${\displaystyle \partial \Delta [n]\to \Delta [n]}$, and let ${\displaystyle WC_{0}}$ be the class of horn inclusions ${\displaystyle \Lambda ^{i}[n]\to \Delta [n]}$. Then the classes of fibrations, acyclic cofibrations, acyclic fibrations, and cofibrations are, respectively, ${\displaystyle WC_{0}^{\perp \ell },WC_{0}^{\perp \ell r},C_{0}^{\perp \ell },C_{0}^{\perp \ell r}}$.^[2]

• Let Ch(R) be the category of chain complexes over a commutative ring R. Let ${\displaystyle C_{0}}$ be the class of maps of form

${\displaystyle \cdots \to 0\to R\to 0\to 0\to \cdots \to \cdots \to R{\xrightarrow {\operatorname {id} }}R\to 0\to 0\to \cdots ,}$

and ${\displaystyle WC_{0}}$ be

${\displaystyle \cdots \to 0\to 0\to 0\to 0\to \cdots \to \cdots \to R{\xrightarrow {\operatorname {id} }}R\to 0\to 0\to \cdots .}$

Then ${\displaystyle WC_{0}^{\perp \ell },WC_{0}^{\perp \ell r},C_{0}^{\perp \ell },C_{0}^{\perp \ell r}}$ are the classes of fibrations, acyclic cofibrations, acyclic fibrations, and cofibrations.^[3]

Elementary examples in various categories[]

In Set,

• ${\displaystyle \{\emptyset \to \{*\}\}^{\perp r}}$ is the class of surjections,

• ${\displaystyle (\{a,b\}\to \{*\})^{\perp r}=(\{a,b\}\to \{*\})^{\perp \ell }}$ is the class of injections.

In the category R-Mod of modules over a commutative ring R,

• ${\displaystyle \{0\to R\}^{\perp r},\{R\to 0\}^{\perp r}}$ is the class of surjections, resp. injections,

• A module M is projective, resp. injective, iff ${\displaystyle 0\to M}$ is in ${\displaystyle \{0\to R\}^{\perp \ell r}}$, resp. ${\displaystyle M\to 0}$ is in ${\displaystyle \{R\to 0\}^{\perp rr}}$.

In the category Grp of groups,

• ${\displaystyle \{\mathbb {Z} \to 0\}^{\perp r}}$, resp. ${\displaystyle \{0\to \mathbb {Z} \}^{\perp r}}$, is the class of injections, resp. surjections (where ${\displaystyle \mathbb {Z} }$ denotes the infinite cyclic group),

• A group F is a free group iff ${\displaystyle 0\to F}$ is in ${\displaystyle \{0\to \mathbb {Z} \}^{\perp r\ell },}$

• A group A is torsion-free iff ${\displaystyle 0\to A}$ is in ${\displaystyle \{n\mathbb {Z} \to \mathbb {Z} :n>0\}^{\perp r},}$

• A subgroup A of B is pure iff ${\displaystyle A\to B}$ is in ${\displaystyle \{n\mathbb {Z} \to \mathbb {Z} :n>0\}^{\perp r}.}$

For a finite group G,

• ${\displaystyle \{0\to {\mathbb {Z} }/p{\mathbb {Z} }\}\perp G\to 1}$ iff the order of G is prime to p,

• ${\displaystyle G\to 1\in (0\to {\mathbb {Z} }/p{\mathbb {Z} })^{\perp rr}}$ iff G is a p-group,

• H is nilpotent iff the diagonal map ${\displaystyle H\to H\times H}$ is in ${\displaystyle (1\to *)^{\perp \ell r}}$ where ${\displaystyle (1\to *)}$ denotes the class of maps ${\displaystyle \{1\to G:G{\text{ arbitrary}}\},}$

• a finite group H is soluble iff ${\displaystyle 1\to H}$ is in ${\displaystyle \{0\to A:A{\text{ abelian}}\}^{\perp \ell r}=\{[G,G]\to G:G{\text{ arbitrary }}\}^{\perp \ell r}.}$

In the category Top of topological spaces, let ${\displaystyle \{0,1\}}$, resp. ${\displaystyle \{0\leftrightarrow 1\}}$ denote the discrete, resp. antidiscrete space with two points 0 and 1. Let ${\displaystyle \{0\to 1\}}$ denote the Sierpinski space of two points where the point 0 is open and the point 1 is closed, and let ${\displaystyle \{0\}\to \{0\to 1\},\{1\}\to \{0\to 1\}}$ etc. denote the obvious embeddings.

• a space X satisfies the separation axiom T₀ iff ${\displaystyle X\to \{*\}}$ is in ${\displaystyle (\{0\leftrightarrow 1\}\to \{*\})^{\perp r},}$

• a space X satisfies the separation axiom T₁ iff ${\displaystyle \emptyset \to X}$ is in ${\displaystyle (\{0\to 1\}\to \{*\})^{\perp r},}$

• ${\displaystyle (\{1\}\to \{0\to 1\})^{\perp \ell }}$ is the class of maps with dense image,

• ${\displaystyle (\{0\to 1\}\to \{*\})^{\perp \ell }}$ is the class of maps ${\displaystyle f:X\to Y}$ such that the topology on A is the pullback of topology on B, i.e. the topology on A is the topology with least number of open sets such that the map is continuous,

• ${\displaystyle (\emptyset \to \{*\})^{\perp r}}$ is the class of surjective maps,

• ${\displaystyle (\emptyset \to \{*\})^{\perp r\ell }}$ is the class of maps of form ${\displaystyle A\to A\cup D}$ where D is discrete,

• ${\displaystyle (\emptyset \to \{*\})^{\perp r\ell \ell }=(\{a\}\to \{a,b\})^{\perp \ell }}$ is the class of maps ${\displaystyle A\to B}$ such that each connected component of B intersects ${\displaystyle \operatorname {Im} A}$,

• ${\displaystyle (\{0,1\}\to \{*\})^{\perp r}}$ is the class of injective maps,

• ${\displaystyle (\{0,1\}\to \{*\})^{\perp \ell }}$ is the class of maps ${\displaystyle f:X\to Y}$ such that the preimage of a connected closed open subset of Y is a connected closed open subset of X, e.g. X is connected iff ${\displaystyle X\to \{*\}}$ is in ${\displaystyle (\{0,1\}\to \{*\})^{\perp \ell }}$,

• for a connected space X, each continuous function on X is bounded iff ${\displaystyle \emptyset \to X\perp \cup _{n}(-n,n)\to \mathbb {R} }$ where ${\displaystyle \cup _{n}(-n,n)\to \mathbb {R} }$ is the map from the disjoint union of open intervals ${\displaystyle (-n,n)}$ into the real line ${\displaystyle \mathbb {R} ,}$

• a space X is Hausdorff iff for any injective map ${\displaystyle \{a,b\}\hookrightarrow X}$, it holds ${\displaystyle \{a,b\}\hookrightarrow X\perp \{a\to x\leftarrow b\}\to \{*\}}$ where ${\displaystyle \{a\leftarrow x\to b\}}$ denotes the three-point space with two open points a and b, and a closed point x,

• a space X is perfectly normal iff ${\displaystyle \emptyset \to X\perp [0,1]\to \{0\leftarrow x\to 1\}}$ where the open interval ${\displaystyle (0,1)}$ goes to x, and ${\displaystyle 0}$ maps to the point ${\displaystyle 0}$, and ${\displaystyle 1}$ maps to the point ${\displaystyle 1}$, and ${\displaystyle \{0\leftarrow x\to 1\}}$ denotes the three-point space with two closed points ${\displaystyle 0,1}$ and one open point x.

In the category of metric spaces with uniformly continuous maps.

• A space X is complete iff ${\displaystyle \{1/n\}_{n\in \mathbb {N} }\to \{0\}\cup \{1/n\}_{n\in \mathbb {N} }\perp X\to \{0\}}$ where ${\displaystyle \{1/n\}_{n\in \mathbb {N} }\to \{0\}\cup \{1/n\}_{n\in \mathbb {N} }}$ is the obvious inclusion between the two subspaces of the real line with induced metric, and ${\displaystyle \{0\}}$ is the metric space consisting of a single point,

• A subspace ${\displaystyle i:A\to X}$ is closed iff ${\displaystyle \{1/n\}_{n\in \mathbb {N} }\to \{0\}\cup \{1/n\}_{n\in \mathbb {N} }\perp A\to X.}$

Notes[]

References[]

• Hovey, Mark (1999). Model Categories.