Subgroup

This article needs additional citations for verification. Please help by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources:  –  ·  ·  · scholar · JSTOR (June 2009) (Learn how and when to remove this template message)

Algebraic structure → Group theory Group theory
Basic notions Subgroup Normal subgroup Quotient group (Semi-)direct product Group homomorphisms kernel image direct sum wreath product simple finite infinite continuous multiplicative additive cyclic abelian dihedral nilpotent solvable action Glossary of group theory List of group theory topics
Finite groups Classification of finite simple groups cyclic alternating Lie type sporadic Cauchy's theorem Lagrange's theorem Sylow theorems Hall's theorem p-group Elementary abelian group Frobenius group Schur multiplier Symmetric group Sn Klein four-group V Dihedral group Dn Quaternion group Q Dicyclic group Dicn
Discrete groups Lattices Integers (${\displaystyle \mathbb {Z} }$) Free group Modular groups PSL(2, ${\displaystyle \mathbb {Z} }$) SL(2, ${\displaystyle \mathbb {Z} }$) Arithmetic group Lattice Hyperbolic group
Topological and Lie groups Solenoid Circle General linear GL(n) Special linear SL(n) Orthogonal O(n) Euclidean E(n) Special orthogonal SO(n) Unitary U(n) Special unitary SU(n) Symplectic Sp(n) G2 F4 E6 E7 E8 Lorentz Poincaré Conformal Diffeomorphism Loop Infinite dimensional Lie group O(∞) SU(∞) Sp(∞)
Algebraic groups Linear algebraic group Reductive group Abelian variety Elliptic curve
v t

In group theory, a branch of mathematics, given a group G under a binary operation ∗, a subset H of G is called a subgroup of G if H also forms a group under the operation ∗. More precisely, H is a subgroup of G if the restriction of ∗ to H × H is a group operation on H. This is often denoted H ≤ G, read as "H is a subgroup of G".

The trivial subgroup of any group is the subgroup {e} consisting of just the identity element.

A proper subgroup of a group G is a subgroup H which is a proper subset of G (that is, H ≠ G). This is often represented notationally by H < G, read as "H is a proper subgroup of G". Some authors also exclude the trivial group from being proper (that is, H ≠ {e}).^[1][2]

If H is a subgroup of G, then G is sometimes called an overgroup of H.

The same definitions apply more generally when G is an arbitrary semigroup, but this article will only deal with subgroups of groups.

Subgroup tests[]

Suppose that G is a group, and H is a subset of G.

• Then H is a subgroup of G if and only if H is nonempty and closed under products and inverses. (Closed under products means that for every a and b in H, the product ab is in H. Closed under inverses means that for every a in H, the inverse a⁻¹ is in H. These two conditions can be combined into one, that for every a and b in H, the element ab⁻¹ is in H, but it is more natural and usually just as easy to test the two closure conditions separately.)^[3]
• When H is finite, the test can be simplified: H is a subgroup if and only if it is nonempty and closed under products. (These conditions alone imply that every element a of H generates a finite cyclic subgroup of H, say of order n, and then the inverse of a is aⁿ⁻¹.)^[4]

Basic properties of subgroups[]

• The identity of a subgroup is the identity of the group: if G is a group with identity e_G, and H is a subgroup of G with identity e_H, then e_H = e_G.
• The inverse of an element in a subgroup is the inverse of the element in the group: if H is a subgroup of a group G, and a and b are elements of H such that ab = ba = e_H, then ab = ba = e_G.
• If H is a subgroup of G, then the inclusion map H → G sending each element a of H to itself is a homomorphism.
• The intersection of subgroups A and B of G is again a subgroup of G.^[5] For example, the intersection of the x-axis and y-axis in R² under addition is the trivial subgroup. More generally, the intersection of an arbitrary collection of subgroups of G is a subgroup of G.
• The union of subgroups A and B is a subgroup if and only if A ⊆ B or B ⊆ A. A non-example: 2Z ∪ 3Z is not a subgroup of Z, because 2 and 3 are elements of this subset whose sum, 5, is not in the subset. Similarly, the union of the x-axis and the y-axis in R² is not a subgroup of R².
• If S is a subset of G, then there exists a smallest subgroup containing S, namely the intersection of all of subgroups containing S; it is denoted by ⟨S⟩ and is called the subgroup generated by S. An element of G is in ⟨S⟩ if and only if it is a finite product of elements of S and their inverses, possibly repeated.
• Every element a of a group G generates a cyclic subgroup ⟨a⟩. If ⟨a⟩ is isomorphic to Z/nZ for some positive integer n, then n is the smallest positive integer for which aⁿ = e, and n is called the order of a. If ⟨a⟩ is isomorphic to Z, then a is said to have infinite order.
• The subgroups of any given group form a complete lattice under inclusion, called the lattice of subgroups. (While the infimum here is the usual set-theoretic intersection, the supremum of a set of subgroups is the subgroup generated by the set-theoretic union of the subgroups, not the set-theoretic union itself.) If e is the identity of G, then the trivial group {e} is the minimum subgroup of G, while the maximum subgroup is the group G itself.

G is the group ${\displaystyle \mathbb {Z} /8\mathbb {Z} }$, the integers mod 8 under addition. The subgroup H contains only 0 and 4, and is isomorphic to ${\displaystyle \mathbb {Z} /2\mathbb {Z} }$. There are four left cosets of H: H itself, 1+H, 2+H, and 3+H (written using additive notation since this is an additive group). Together they partition the entire group G into equal-size, non-overlapping sets. The index [G : H] is 4.

Cosets and Lagrange's theorem[]

Given a subgroup H and some a in G, we define the left coset aH = {ah : h in H}. Because a is invertible, the map φ : H → aH given by φ(h) = ah is a bijection. Furthermore, every element of G is contained in precisely one left coset of H; the left cosets are the equivalence classes corresponding to the equivalence relation a₁ ~ a₂ if and only if a₁⁻¹a₂ is in H. The number of left cosets of H is called the index of H in G and is denoted by [G : H].

Lagrange's theorem states that for a finite group G and a subgroup H,

${\displaystyle [G:H]={|G| \over |H|}}$

where |G| and |H| denote the orders of G and H, respectively. In particular, the order of every subgroup of G (and the order of every element of G) must be a divisor of |G|.^[6][7]

Right cosets are defined analogously: Ha = {ha : h in H}. They are also the equivalence classes for a suitable equivalence relation and their number is equal to [G : H].

If aH = Ha for every a in G, then H is said to be a normal subgroup. Every subgroup of index 2 is normal: the left cosets, and also the right cosets, are simply the subgroup and its complement. More generally, if p is the lowest prime dividing the order of a finite group G, then any subgroup of index p (if such exists) is normal.

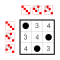
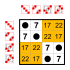
Example: Subgroups of Z₈[]

Let G be the cyclic group Z₈ whose elements are

${\displaystyle G=\left\{0,4,2,6,1,5,3,7\right\}}$

and whose group operation is addition modulo 8. Its Cayley table is

This group has two nontrivial subgroups: ■ J = {0, 4} and ■ H = {0, 4, 2, 6} , where J is also a subgroup of H. The Cayley table for H is the top-left quadrant of the Cayley table for G; The Cayley table for J is the top-left quadrant of the Cayley table for H. The group G is cyclic, and so are its subgroups. In general, subgroups of cyclic groups are also cyclic.

Example: Subgroups of S₄[]

Let S₄ be the symmetric group on 4 elements. Below are all the subgroups of S₄, listed according to the number of elements, in decreasing order.

24 elements[]

The whole group S₄ is a subgroup of S₄, of order 24. Its Cayley table is

The symmetric group S4 showing all permutations of 4 elements

All 30 subgroups Simplified Hasse diagrams of the lattice of subgroups of S4

12 elements[]

The alternating group A₄ showing only the even permutations

Subgroups:

8 elements[]

Dihedral group of order 8 Subgroups:

Dihedral group of order 8 Subgroups: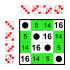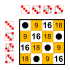

Dihedral group of order 8 Subgroups: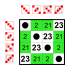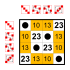

6 elements[]

Symmetric group S3 Subgroup:

Symmetric group S3 Subgroup:

Symmetric group S3 Subgroup: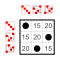

Symmetric group S3 Subgroup: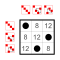

4 elements[]

Klein four-group

Klein four-group

Klein four-group

Klein four-group

Cyclic group Z4

Cyclic group Z4

Cyclic group Z4

3 elements[]

Cyclic group Z3

Cyclic group Z3

Cyclic group Z3

Cyclic group Z3

2 elements[]

Each element s of order 2 in S₄ generates a subgroup {1,s} of order 2. There are 9 such elements: the ${\displaystyle {\binom {4}{2}}=6}$ transpositions (2-cycles) and the three elements (12)(34), (13)(24), (14)(23).

1 element[]

The trivial subgroup is the unique subgroup of order 1 in S₄.

Other examples[]

• The even integers form a subgroup 2Z of the integer ring Z: the sum of two even integers is even, and the negative of an even integer is even.
• An ideal in a ring ${\displaystyle R}$ is a subgroup of the additive group of ${\displaystyle R}$.
• A linear subspace of a vector space is a subgroup of the additive group of vectors.
• In an abelian group, the elements of finite order form a subgroup called the torsion subgroup.

See also[]

• Cartan subgroup
• Fitting subgroup
• Stable subgroup
• Fixed-point subgroup

Notes[]

References[]

• Jacobson, Nathan (2009), Basic algebra, vol. 1 (2nd ed.), Dover, ISBN 978-0-486-47189-1.
• Hungerford, Thomas (1974), Algebra (1st ed.), Springer-Verlag, ISBN 9780387905181.
• Artin, Michael (2011), Algebra (2nd ed.), Prentice Hall, ISBN 9780132413770.
• Dummit, David S.; Foote, Richard M. (2004). Abstract algebra (3rd ed.). Hoboken, NJ: Wiley. ISBN 9780471452348. OCLC 248917264.
• Kurzweil, Hans; Stellmacher, Bernd (1998). Theorie der endlichen Gruppen. Springer-Lehrbuch. doi:10.1007/978-3-642-58816-7.