Mrs. Miniver's problem
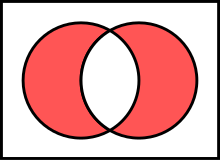
Mrs. Miniver's problem is a geometry problem about the area of circles. It asks how to place two circles and of given radii in such a way that the lens formed by intersecting their two interiors has equal area to the symmetric difference of and (the area contained in one but not both circles).[1]
Origin[]
The problem derives from "A Country House Visit", one of Jan Struther's newspaper articles featuring her character Mrs. Miniver. According to the story:
She saw every relationship as a pair of intersecting circles. It would seem at first glance that the more they overlapped the better the relationship; but this is not so. Beyond a certain point the law of diminishing returns sets in, and there are not enough private resources left on either side to enrich the life that is shared. Probably perfection is reached when the area of the two outer crescents, added together, is exactly equal to that of the leaf-shaped piece in the middle. On paper there must be some neat mathematical formula for arriving at this; in life, none.[2]
Louis A. Graham and Clifton Fadiman formalized the mathematics of the problem and popularized it among recreational mathematicians.[1][3]
Solution[]
The problem can be solved by cutting the lune along the line segment between the two crossing points of the circles, into two circular segments, and using the formula for the area of a circular segment to relate the distance between the crossing points to the total area that the problem requires the lune to have. This gives a transcendental equation for the distance between crossing points but it can be solved numerically.[1][4] In the case of two circles of equal size, these equations can be simplified somewhat. The rhombus formed by the two circle centers and the two crossing points, with side lengths equal to the radius, has an angle at the circle centers, found by solving the equation
See also[]
- Goat problem, another problem of equalizing the areas of circular lunes and lenses
References[]
- ^ a b c Graham, Louis A. (1959), "3: Mrs. Miniver's problem", Ingenious Mathematical Problems and Methods, Dover Books on Mathematics, Dover Publications, pp. 64–66, ISBN 978-0-486-28293-0
- ^ Struther, Jan, "A Country House Visit", Mrs. Miniver, University of Pennsylvania, retrieved 2022-03-10. Originally published as part of a series of columns in The Times, 1937, and in the book Mrs. Miniver, Chatto and Windus, London, 1939.
- ^ Fadiman, Clifton (1962), "The Miniver problem", The Mathematical Magpie, Simon & Schuster, pp. 298–300
- ^ a b Alsina, Claudi; Nelsen, Roger B. (2011), "11.8: Mrs. Miniver's problem", Icons of Mathematics: An Exploration of Twenty Key Images, Dolciani Mathematical Expositions, vol. 56, American Mathematical Society, pp. 141–142, ISBN 978-1-4704-5616-0
- Circles
- Area
- Mathematical problems




