Regular skew apeirohedron

In geometry, a regular skew apeirohedron is an infinite regular skew polyhedron, with either skew regular faces or skew regular vertex figures.

History[]

According to Coxeter, in 1926 John Flinders Petrie generalized the concept of regular skew polygons (nonplanar polygons) to finite regular skew polyhedra in 4-dimensions, and infinite regular skew apeirohedra in 3-dimensions (described here).

Coxeter identified 3 forms, with planar faces and skew vertex figures, two are complements of each other. They are all named with a modified Schläfli symbol {l,m|n}, where there are l-gonal faces, m faces around each vertex, with holes identified as n-gonal missing faces.

Coxeter offered a modified Schläfli symbol {l,m|n} for these figures, with {l,m} implying the vertex figure, m l-gons around a vertex, and n-gonal holes. Their vertex figures are skew polygons, zig-zagging between two planes.

The regular skew polyhedra, represented by {l,m|n}, follow this equation:

• 2 sin(π/l) · sin(π/m) = cos(π/n)

Regular skew apeirohedra of Euclidean 3-space[]

The three Euclidean solutions in 3-space are {4,6|4}, {6,4|4}, and {6,6|3}. John Conway named them mucube, muoctahedron, and mutetrahedron respectively for multiple cube, octahedron, and tetrahedron.^[1]

1. Mucube: {4,6|4}: 6 squares about each vertex (related to cubic honeycomb, constructed by cubic cells, removing two opposite faces from each, and linking sets of six together around a faceless cube.)
2. Muoctahedron: {6,4|4}: 4 hexagons about each vertex (related to bitruncated cubic honeycomb, constructed by truncated octahedron with their square faces removed and linking hole pairs of holes together.)
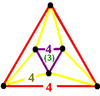
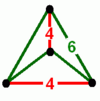
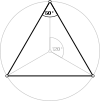
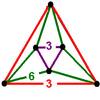
3. Mutetrahedron: {6,6|3}: 6 hexagons about each vertex (related to quarter cubic honeycomb, constructed by truncated tetrahedron cells, removing triangle faces, and linking sets of four around a faceless tetrahedron.)

Coxeter gives these regular skew apeirohedra {2q,2r|p} with extended chiral symmetry [[(p,q,p,r)]⁺] which he says is isomorphic to his abstract group (2q,2r|2,p). The related honeycomb has the extended symmetry [[(p,q,p,r)]].^[2]

Compact regular skew apeirohedra

Coxeter group symmetry	Apeirohedron {p,q|l}	Image	Face {p}	Hole {l}	Vertex figure	Related honeycomb
[[4,3,4]] [[4,3,4]+]	{4,6|4} Mucube	animation				t0,3{4,3,4}
	{6,4|4} Muoctahedron	animation				2t{4,3,4}
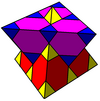
[[3[4]]] [[3[4]]+]	{6,6|3} Mutetrahedron	animation				q{4,3,4}

Regular skew apeirohedra in hyperbolic 3-space[]

In 1967, C. W. L. Garner identified 31 hyperbolic skew apeirohedra with regular skew polygon vertex figures, found in a similar search to the 3 above from Euclidean space.^[3]

These represent 14 compact and 17 paracompact regular skew polyhedra in hyperbolic space, constructed from the symmetry of a subset of linear and cyclic Coxeter groups graphs of the form [[(p,q,p,r)]], These define regular skew polyhedra {2q,2r|p} and dual {2r,2q|p}. For the special case of linear graph groups r = 2, this represents the Coxeter group [p,q,p]. It generates regular skews {2q,4|p} and {4,2q|p}. All of these exist as a subset of faces of the convex uniform honeycombs in hyperbolic space.

The skew apeirohedron shares the same antiprism vertex figure with the honeycomb, but only the zig-zag edge faces of the vertex figure are realized, while the other faces make "holes".

14 Compact regular skew apeirohedra

Coxeter group	Apeirohedron {p,q|l}	Face {p}	Hole {l}	Honeycomb	Vertex figure		Apeirohedron {p,q|l}	Face {p}	Hole {l}	Honeycomb	Vertex figure
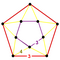
[3,5,3]	{10,4|3}			2t{3,5,3}			{4,10|3}			t0,3{3,5,3}
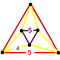
[5,3,5]	{6,4|5}			2t{5,3,5}			{4,6|5}			t0,3{5,3,5}
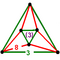
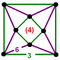
[(4,3,3,3)]	{8,6|3}			ct{(4,3,3,3)}			{6,8|3}			ct{(3,3,4,3)}
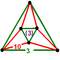
[(5,3,3,3)]	{10,6|3}			ct{(5,3,3,3)}			{6,10|3}			ct{(3,3,5,3)}
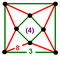
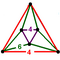
[(4,3,4,3)]	{8,8|3}			ct{(4,3,4,3)}			{6,6|4}			ct{(3,4,3,4)}
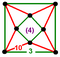
[(5,3,4,3)]	{8,10|3}			ct{(4,3,5,3)}			{10,8|3}			ct{(5,3,4,3)}
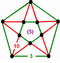
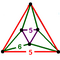
[(5,3,5,3)]	{10,10|3}			ct{(5,3,5,3)}			{6,6|5}			ct{(3,5,3,5)}

17 Paracompact regular skew apeirohedra

Coxeter group	Apeirohedron {p,q|l}	Face {p}	Hole {l}	Honeycomb	Vertex figure		Apeirohedron {p,q|l}	Face {p}	Hole {l}	Honeycomb	Vertex figure
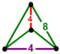
[4,4,4]	{8,4|4}			2t{4,4,4}			{4,8|4}			t0,3{4,4,4}
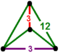
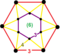
[3,6,3]	{12,4|3}			2t{3,6,3}			{4,12|3}			t0,3{3,6,3}
[6,3,6]	{6,4|6}			2t{6,3,6}			{4,6|6}			t0,3{6,3,6}
[(4,4,4,3)]	{8,6|4}			ct{(4,4,3,4)}			{6,8|4}			ct{(3,4,4,4)}
[(4,4,4,4)]	{8,8|4}			q{4,4,4}
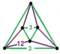
[(6,3,3,3)]	{12,6|3}			ct{(6,3,3,3)}			{6,12|3}			ct{(3,3,6,3)}
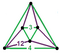
[(6,3,4,3)]	{12,8|3}			ct{(6,3,4,3)}			{8,12|3}			ct{(4,3,6,3)}
[(6,3,5,3)]	{12,10|3}			ct{(6,3,5,3)}			{10,12|3}			ct{(5,3,6,3)}
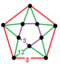
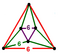
[(6,3,6,3)]	{12,12|3}			ct{(6,3,6,3)}			{6,6|6}			ct{(3,6,3,6)}

See also[]

• Skew apeirohedron
• Regular skew polyhedron
• Tetrastix

References[]

• Petrie–Coxeter Maps Revisited PDF, Isabel Hubard, Egon Schulte, Asia Ivic Weiss, 2005
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5,
• Peter McMullen, Four-Dimensional Regular Polyhedra, Discrete & Computational Geometry September 2007, Volume 38, Issue 2, pp 355–387
• Coxeter, Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2]
  • (Paper 2) H.S.M. Coxeter, "The Regular Sponges, or Skew Polyhedra", Scripta Mathematica 6 (1939) 240–244.
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
  • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
• Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues, Proceedings of the London Mathematics Society, Ser. 2, Vol 43, 1937.)
  • Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proc. London Math. Soc. 43, 33–62, 1937.