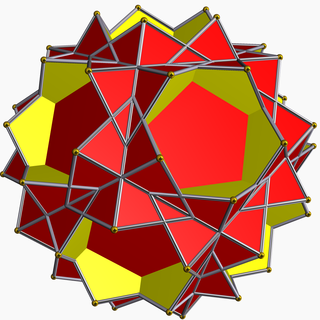
Small stellated truncated dodecahedron

Small stellated truncated dodecahedron

Type	Uniform star polyhedron
Elements	F = 24, E = 90 V = 60 (χ = −6)
Faces by sides	12{5}+12{10/3}
Wythoff symbol	2 5 \| 5/3 2 5/4 \| 5/3
Symmetry group	I_h, [5,3], *532
Index references	U₅₈, C₇₄, W₉₇
Dual polyhedron	Great pentakis dodecahedron
Vertex figure	5.10/3.10/3
	Quit Sissid

3D model of a small stellated truncated dodecahedron

In geometry, the small stellated truncated dodecahedron (or quasitruncated small stellated dodecahedron or small stellatruncated dodecahedron) is a nonconvex uniform polyhedron, indexed as U₅₈. It has 24 faces (12 pentagons and 12 decagrams), 90 edges, and 60 vertices.^[1] It is given a Schläfli symbol t{5⁄3,5}, and Coxeter diagram .

Related polyhedra[]

It shares its vertex arrangement with three other uniform polyhedra: the convex rhombicosidodecahedron, the small dodecicosidodecahedron and the small rhombidodecahedron.

It also has the same vertex arrangement as the uniform compounds of 6 or 12 pentagrammic prisms.

Rhombicosidodecahedron	Small dodecicosidodecahedron	Small rhombidodecahedron
Small stellated truncated dodecahedron	Compound of six pentagrammic prisms	Compound of twelve pentagrammic prisms