Symmetric relation

This article needs additional citations for verification. Please help by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources:  –  ·  ·  · scholar · JSTOR (July 2021) (Learn how and when to remove this template message)

showTransitive Binary Relations
Symmetric Antisymmetric Connected Well-founded Has joins Has meets Reflexive Irreflexive Asymmetric Also known as: Total, Semiconnex Anti-reflexive Equivalence relation ✓ ✗ ✗ ✗ ✗ ✗ ✓ ✗ ✗ Preorder (Quasiorder) ✗ ✗ ✗ ✗ ✗ ✗ ✓ ✗ ✗ Partial order ✗ ✓ ✗ ✗ ✗ ✗ ✓ ✗ ✗ Total preorder ✗ ✗ ✓ ✗ ✗ ✗ ✓ ✗ ✗ Total order ✗ ✓ ✓ ✗ ✗ ✗ ✓ ✗ ✗ Prewellordering ✗ ✗ ✓ ✓ ✗ ✗ ✓ ✗ ✗ Well-quasi-ordering ✗ ✗ ✗ ✓ ✗ ✗ ✓ ✗ ✗ Well-ordering ✗ ✓ ✓ ✓ ✗ ✗ ✓ ✗ ✗ Lattice ✗ ✓ ✗ ✗ ✓ ✓ ✓ ✗ ✗ Join-semilattice ✗ ✓ ✗ ✗ ✓ ✗ ✓ ✗ ✗ Meet-semilattice ✗ ✓ ✗ ✗ ✗ ✓ ✓ ✗ ✗ Strict partial order ✗ ✗ ✗ ✗ ✗ ✗ ✗ ✓ ✓ Strict weak order ✗ ✗ ✗ ✗ ✗ ✗ ✗ ✓ ✓ Strict total order ✗ ✗ ✓ ✗ ✗ ✗ ✗ ✓ ✓ Symmetric Antisymmetric Connected Well-founded Has joins Has meets Reflexive Irreflexive Asymmetric Definitions: ${\displaystyle \scriptstyle {{\text{For all}}\,a,b\,{\text{and}}\,S\neq \varnothing :}}$ ${\displaystyle \scriptstyle {aRb\Rightarrow bRa}}$ ${\displaystyle \scriptstyle {aRb\,{\text{and}}\,bRa\Rightarrow a=b}}$ ${\displaystyle \scriptstyle {a\neq b\Rightarrow aRb\,{\text{or}}\,bRa}}$ ${\displaystyle \scriptstyle {\min S\,{\text{exists}}}}$ ${\displaystyle \scriptstyle {a\vee b\,{\text{exists}}}}$ ${\displaystyle \scriptstyle {a\wedge b\,{\text{exists}}}}$ ${\displaystyle \scriptstyle {aRa}}$ ${\displaystyle \scriptstyle {{\text{not}}\,aRa}}$ ${\displaystyle \scriptstyle {aRb\Rightarrow {\text{not}}\,bRa}}$
All definitions tacitly require the homogeneous relation ${\displaystyle R}$ be transitive: ${\displaystyle \scriptstyle {{\text{For all}}\,a,b,c,{\text{ if }}aRb{\text{ and }}bRc{\text{ then }}aRc}.}$ A "✓" indicates that the column property is required in the row definition. For example, the definition of an equivalence relation requires it to be symmetric. Listed here are additional properties that a homogeneous relation may satisfy.

A symmetric relation is a type of binary relation. An example is the relation "is equal to", because if a = b is true then b = a is also true. Formally, a binary relation R over a set X is symmetric if:

${\displaystyle \forall a,b\in X(aRb\Leftrightarrow bRa).}$^[1]

If R^T represents the converse of R, then R is symmetric if and only if R = R^T.^{[citation needed]}

Symmetry, along with reflexivity and transitivity, are the three defining properties of an equivalence relation.^[1]

Examples[]

In mathematics[]

• "is equal to" (equality) (whereas "is less than" is not symmetric)
• "is comparable to", for elements of a partially ordered set
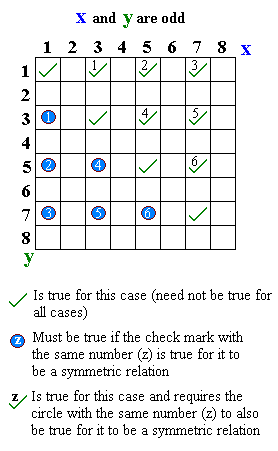
• "... and ... are odd":

Outside mathematics[]

• "is married to" (in most legal systems)
• "is a fully biological sibling of"
• "is a homophone of"
• "is co-worker of"
• "is teammate of"

Relationship to asymmetric and antisymmetric relations[]

By definition, a nonempty relation cannot be both symmetric and asymmetric (where if a is related to b, then b cannot be related to a (in the same way)). However, a relation can be neither symmetric nor asymmetric, which is the case for "is less than or equal to" and "preys on").

Symmetric and antisymmetric (where the only way a can be related to b and b be related to a is if a = b) are actually independent of each other, as these examples show.

Properties[]

• A symmetric and transitive relation is always quasireflexive.^{[citation needed]}

• A symmetric, transitive, and reflexive relation is called an equivalence relation.^[1]

• One way to conceptualize a symmetric relation in graph theory is that a symmetric relation is an edge, with the edge's two vertices being the two entities so related. Thus, symmetric relations and undirected graphs are combinatorially equivalent objects.^{[citation needed]}

References[]

See also[]

• Commutative property – Property allowing changing the order of the operands of an operation
• Symmetry in mathematics – Symmetry in mathematics
• Symmetry – Mathematical invariance under transformations