Truncated octahedral prism

Truncated octahedral prism
Type	Prismatic uniform 4-polytope
Uniform index	54
Schläfli symbol	t0,1,3{3,4,2} or t{3,4}×{} t0,1,2,3{3,3,2} or tr{3,3}×{}
Coxeter-Dynkin
Cells	16: 2 4.6.6 6 {4,3} 8 {}x{6}
Faces	64: 48 {4} 16 {6}
Edges	96
Vertices	48
Vertex figure	Isosceles-triangular pyramid
Symmetry group	[3,4,2], order 96 [3,3,2], order 48
Dual polytope
Properties	convex

In 4-dimensional geometry, a truncated octahedral prism or omnitruncated tetrahedral prism is a convex uniform 4-polytope. This 4-polytope has 16 cells (2 truncated octahedra connected by 6 cubes, 8 hexagonal prisms.) It has 64 faces (48 squares and 16 hexagons), and 96 edges and 48 vertices.

It has two symmetry constructions, one from the truncated octahedron, and one as an omnitruncation of the tetrahedron.

It is one of 18 uniform polyhedral prisms created by using uniform prisms to connect pairs of parallel Platonic solids and Archimedean solids.

Images[]

Net	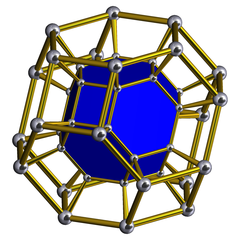Schlegel diagram

Alternative names[]

• Truncated octahedral dyadic prism (Norman W. Johnson)
• Truncated octahedral hyperprism
• Tope (Jonathan Bowers: for truncated octahedral prism)

Related polytopes[]

The snub tetrahedral prism (also called an icosahedral prism), , sr{3,3}×{ }, is related to this polytope just like a snub tetrahedron (icosahedron), is the alternation of the truncated octahedron in its tetrahedral symmetry . The snub tetrahedral prism has symmetry [(3,3)⁺,2], order 24, although as an icosahedral prism, its full symmetry is [5,3,2], order 240.

Also related, the full snub tetrahedral antiprism or omnisnub tetrahedral antiprism is defined as an alternation of an omnitruncated tetrahedral prism, represented by ${\displaystyle s\left\{{\begin{array}{l}3\\3\\2\end{array}}\right\}}$ = ht_0,1,2,3{3,3,2}, or , although it cannot be constructed as a uniform 4-polytope. It can also be seen as an alternated truncated octahedral prism or pyritohedral icosahedral antiprism, . It has 2 icosahedra connected by 6 tetrahedra and 8 octahedra, with 24 irregular tetrahedra in the alternated gaps. In total it has 40 cells, 112 triangular faces, 96 edges, and 24 vertices. It has [4,(3,2)⁺] symmetry, order 48, and also [3,3,2]⁺ symmetry, order 24.

A construction exists with two regular icosahedra in snub positions with two edge lengths in a ratio of around 0.831 : 1.

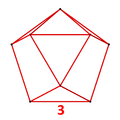
Vertex figure for the omnisnub tetrahedral antiprism

See also[]

• Truncated 16-cell,

External links[]

• 6. Convex uniform prismatic polychora - Model 54, George Olshevsky.
• Klitzing, Richard. "4D uniform polytopes (polychora) x x3x3x - tope".

This 4-polytope article is a stub. You can help Wikipedia by .

• v
• t