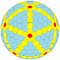
Truncated pentakis dodecahedron

From Wikipedia, the free encyclopedia
Truncated pentakis dodecahedron
Conway polyhedron Dk6k5tI.png
Conway notation tkD
Goldberg polyhedron GPV(3,0) or {5+,3}3,0
Fullerene C180[1]
Faces 92:
12 pentagons
20+60 hexagons
Edges 270 (2 types)
Vertices 180 (2 types)
Vertex configuration (60) 5.6.6
(120) 6.6.6
Symmetry group Icosahedral (Ih)
Dual polyhedron Pentahexakis truncated icosahedron
Properties convex

The truncated pentakis dodecahedron is a convex polyhedron constructed as a truncation of the pentakis dodecahedron. It is Goldberg polyhedron GV(3,0), with pentagonal faces separated by an edge-direct distance of 3 steps.

Related polyhedra[]

It is in an infinite sequence of Goldberg polyhedra:

Index GP(1,0) GP(2,0) GP(3,0) GP(4,0) GP(5,0) GP(6,0) GP(7,0) GP(8,0)...
Image Uniform polyhedron-53-t0.png
D 		Truncated rhombic triacontahedron.png
kD 		Conway polyhedron Dk6k5tI.png
tkD 		Conway polyhedron dk6k5at5daD.png Goldberg polyhedron 5 0.png Conway polyhedron tkt5daD.png Goldberg polyhedron 7 0.png Conway polyhedron dk6k5adk6k5at5daD.png
Duals Uniform polyhedron-53-t2.png
I 		Conway polyhedron k5aD.png
cD 		Conway polyhedron K6k5tI.png
ktI 		Conway polyhedron k6k5at5daD.png Conway polyhedron kdkt5daD.png

See also[]

References[]

  1. ^ C180 Isomers
  • Deza, A.; Deza, M.; Grishukhin, V. (1998), "Fullerenes and coordination polyhedra versus half-cube embeddings", Discrete Mathematics, 192 (1): 41–80, doi:10.1016/S0012-365X(98)00065-X, archived from the original on 2007-02-06.
  • Antoine Deza, Michel Deza, Viatcheslav Grishukhin, Fullerenes and coordination polyhedra versus half-cube embeddings, 1998 PDF [1]

External links[]

Retrieved from ""