Shapley–Folkman lemma

The Shapley–Folkman lemma is illustrated by the Minkowski addition of four sets. The point (+) in the convex hull of the Minkowski sum of the four non-convex sets (right) is the sum of four points (+) from the (left-hand) sets—two points in two non-convex sets plus two points in the convex hulls of two sets. The convex hulls are shaded pink. The original sets each have exactly two points (shown as red dots).^[1]

The Shapley–Folkman lemma is a result in convex geometry with applications in mathematical economics that describes the Minkowski addition of sets in a vector space. Minkowski addition is defined as the addition of the sets' members: for example, adding the set consisting of the integers zero and one to itself yields the set consisting of zero, one, and two:

{0, 1} + {0, 1} = {0 + 0, 0 + 1, 1 + 0, 1 + 1} = {0, 1, 2}.

The Shapley–Folkman lemma and related results provide an affirmative answer to the question, "Is the sum of many sets close to being convex?"^[2] A set is defined to be convex if every line segment joining two of its points is a subset in the set: For example, the solid disk ${\displaystyle \bullet }$ is a convex set but the circle ${\displaystyle \circ }$ is not, because the line segment joining two distinct points ${\displaystyle \oslash }$ is not a subset of the circle. The Shapley–Folkman lemma suggests that if the number of summed sets exceeds the dimension of the vector space, then their Minkowski sum is approximately convex.^[1]

The Shapley–Folkman lemma was introduced as a step in the proof of the Shapley–Folkman theorem, which states an upper bound on the distance between the Minkowski sum and its convex hull. The convex hull of a set Q is the smallest convex set that contains Q. This distance is zero if and only if the sum is convex. The theorem's bound on the distance depends on the dimension D and on the shapes of the summand-sets, but not on the number of summand-sets N, when N > D. The shapes of a subcollection of only D summand-sets determine the bound on the distance between the Minkowski average of N sets

1⁄N (Q₁ + Q₂ + ... + Q_N)

and its convex hull. As N increases to infinity, the bound decreases to zero (for summand-sets of uniformly bounded size).^[3] The Shapley–Folkman theorem's upper bound was decreased by Starr's corollary (alternatively, the Shapley–Folkman–Starr theorem).

The lemma of Lloyd Shapley and Jon Folkman was first published by the economist Ross M. Starr, who was investigating the existence of economic equilibria while studying with Kenneth Arrow.^[1] In his paper, Starr studied a convexified economy, in which non-convex sets were replaced by their convex hulls; Starr proved that the convexified economy has equilibria that are closely approximated by "quasi-equilibria" of the original economy; moreover, he proved that every quasi-equilibrium has many of the optimal properties of true equilibria, which are proved to exist for convex economies. Following Starr's 1969 paper, the Shapley–Folkman–Starr results have been widely used to show that central results of (convex) economic theory are good approximations to large economies with non-convexities; for example, quasi-equilibria closely approximate equilibria of a convexified economy. "The derivation of these results in general form has been one of the major achievements of postwar economic theory", wrote Roger Guesnerie.^[4] The topic of non-convex sets in economics has been studied by many Nobel laureates, besides Lloyd Shapley who won the prize in 2012: Arrow (1972), Robert Aumann (2005), Gérard Debreu (1983), Tjalling Koopmans (1975), Paul Krugman (2008), and Paul Samuelson (1970); the complementary topic of convex sets in economics has been emphasized by these laureates, along with Leonid Hurwicz, Leonid Kantorovich (1975), and Robert Solow (1987).

The Shapley–Folkman lemma has applications also in optimization and probability theory.^[3] In optimization theory, the Shapley–Folkman lemma has been used to explain the successful solution of minimization problems that are sums of many functions.^[5][6] The Shapley–Folkman lemma has also been used in proofs of the "law of averages" for random sets, a theorem that had been proved for only convex sets.^[7]

Introductory example[]

For example, the subset of the integers {0, 1, 2} is contained in the interval of real numbers [0, 2], which is convex. The Shapley–Folkman lemma implies that every point in [0, 2] is the sum of an integer from {0, 1} and a real number from [0, 1].^[8]

The distance between the convex interval [0, 2] and the non-convex set {0, 1, 2} equals one-half

1/2 = |1 − 1/2| = |0 − 1/2| = |2 − 3/2| = |1 − 3/2|.

However, the distance between the average Minkowski sum

1/2 ( {0, 1} + {0, 1} ) = {0, 1/2, 1}

and its convex hull [0, 1] is only 1/4, which is half the distance (1/2) between its summand {0, 1} and [0, 1]. As more sets are added together, the average of their sum "fills out" its convex hull: The maximum distance between the average and its convex hull approaches zero as the average includes more summands.^[8]

Preliminaries[]

The Shapley–Folkman lemma depends upon the following definitions and results from convex geometry.

Real vector spaces[]

A real vector space of two dimensions can be given a Cartesian coordinate system in which every point is identified by an ordered pair of real numbers, called "coordinates", which are conventionally denoted by x and y. Two points in the Cartesian plane can be added coordinate-wise

(x₁, y₁) + (x₂, y₂) = (x₁+x₂, y₁+y₂);

further, a point can be multiplied by each real number λ coordinate-wise

λ (x, y) = (λx, λy).

More generally, any real vector space of (finite) dimension D can be viewed as the set of all D-tuples of D real numbers { (v₁, v₂, . . . , v_D) } on which two operations are defined: vector addition and multiplication by a real number. For finite-dimensional vector spaces, the operations of vector addition and real-number multiplication can each be defined coordinate-wise, following the example of the Cartesian plane.^[9]

Convex sets[]

In a convex set Q, the line segment connecting any two of its points is a subset of Q.

In a non-convex set Q, a point in some line-segment joining two of its points is not a member of Q.

Line segments test whether a subset be convex.

In a real vector space, a non-empty set Q is defined to be convex if, for each pair of its points, every point on the line segment that joins them is still in Q. For example, a solid disk ${\displaystyle \bullet }$ is convex but a circle ${\displaystyle \circ }$ is not, because it does not contain a line segment joining its points ${\displaystyle \oslash }$; the non-convex set of three integers {0, 1, 2} is contained in the interval [0, 2], which is convex. For example, a solid cube is convex; however, anything that is hollow or dented, for example, a crescent shape, is non-convex. The empty set is convex, either by definition^[10] or vacuously, depending on the author.

More formally, a set Q is convex if, for all points v₀ and v₁ in Q and for every real number λ in the unit interval [0,1], the point

(1 − λ) v₀ + λv₁

is a member of Q.

By mathematical induction, a set Q is convex if and only if every convex combination of members of Q also belongs to Q. By definition, a convex combination of an indexed subset {v₀, v₁, . . . , v_D} of a vector space is any weighted average λ₀v₀ + λ₁v₁ + . . . + λ_Dv_D, for some indexed set of non-negative real numbers {λ_d} satisfying the equation λ₀ + λ₁ + . . .  + λ_D = 1.^[11]

The definition of a convex set implies that the intersection of two convex sets is a convex set. More generally, the intersection of a family of convex sets is a convex set. In particular, the intersection of two disjoint sets is the empty set, which is convex.^[10]

Convex hull[]

In the convex hull of the red set, each blue point is a convex combination of some red points.

For every subset Q of a real vector space, its convex hull Conv(Q) is the minimal convex set that contains Q. Thus Conv(Q) is the intersection of all the convex sets that cover Q. The convex hull of a set can be equivalently defined to be the set of all convex combinations of points in Q.^[12] For example, the convex hull of the set of integers {0,1} is the closed interval of real numbers [0,1], which contains the integer end-points.^[8] The convex hull of the unit circle is the closed unit disk, which contains the unit circle.

Minkowski addition[]

Minkowski addition of sets. The sum of the squares ${\displaystyle Q_{1}=[0,1]^{2}}$ and ${\displaystyle Q_{2}=[1,2]^{2}}$ is the square ${\displaystyle Q_{1}+Q_{2}=[1,3]^{2}2}$.

In any vector space (or algebraic structure with addition), ${\displaystyle X}$, the Minkowski sum of two non-empty sets ${\displaystyle A,B\subseteq X}$ is defined to be the element-wise operation ${\displaystyle A+B:=\{x+y\mid x\in A,~y\in B\}.}$ (See also.^[13]) For example

${\displaystyle \{0,1\}+\{0,1\}=\{0+0,0+1,1+0,1+1\}=\{0,1,2\}}$

This operation is clearly commutative and associative on the collection of non-empty sets. All such operations extend in a well-defined manner to recursive forms ${\displaystyle \sum _{n=1}^{N}Q_{n}=Q_{1}+Q_{2}+\ldots +Q_{N}.}$ By the principle of induction it is easy to see that^[14]

${\displaystyle \sum _{n=1}^{N}Q_{n}=\{\sum _{n=1}^{N}q_{n}\mid q_{n}\in Q_{n},~1\leq n\leq N\}.}$

Convex hulls of Minkowski sums[]

Minkowski addition behaves well with respect to taking convex hulls. Specifically, for all subsets ${\displaystyle A,B\subseteq X}$ of a real vector space, ${\displaystyle X}$, the convex hull of their Minkowski sum is the Minkowski sum of their convex hulls. That is,

${\displaystyle \mathrm {Conv} (A+B)=\mathrm {Conv} (A)+\mathrm {Conv} (B).}$

And by induction it follows that

${\displaystyle \mathrm {Conv} (\sum _{n=1}^{N}Q_{n})=\sum _{n=1}^{N}\mathrm {Conv} (Q_{n})}$

for any ${\displaystyle N\in \mathbb {N} }$ and non-empty subsets ${\displaystyle Q_{n}\subseteq X}$, ${\displaystyle 1\leq n\leq N}$.^[15][16]

Statements[]

Minkowski addition and convex hulls. The sixteen dark-red points (on the right) form the Minkowski sum of the four non-convex sets (on the left), each of which consists of a pair of red points. Their convex hulls (shaded pink) contain plus-signs (+): The right plus-sign is the sum of the left plus-signs.

By the preceding identity, for every point ${\displaystyle x\in \mathrm {Conv} (\sum _{n=1}^{N}Q_{n})}$ there exist elements in the convex hulls, ${\displaystyle q_{n}(x)\in \mathrm {Conv} (Q_{n})}$ for ${\displaystyle 1\leq n\leq N}$, dependent upon ${\displaystyle x}$, and such that ${\displaystyle \sum _{n=1}^{N}q_{n}(x)=x}$.

Lemma of Shapley and Folkman[]

A Winner of the 2012 Nobel Award in Economics, Lloyd Shapley proved the Shapley–Folkman lemma with Jon Folkman.^[1]

Working with the above setup, the Shapley–Folkman lemma states that in the above representation

${\displaystyle x=\sum _{n=1}^{N}q_{n}(x)}$

at most ${\displaystyle D}$ of the summands ${\displaystyle q_{n}(x)}$ need to be taken strictly from the convex hulls. That is, there exists a representation of the above form, such that ${\displaystyle |\{l\leq n\leq N\mid q_{n}(x)\in \mathrm {Conv} (Q_{n})\setminus Q_{n}\}|\leq D}$. Shuffling indexes if necessary, this means that the point has a representation

${\displaystyle x=\sum _{n=1}^{D}q_{n}(x)+\sum _{n=D+1}^{N}q_{n}(x)}$

where ${\displaystyle q_{n}\in \mathrm {Conv} (Q_{n})}$ for ${\displaystyle 1\leq n\leq D}$ and ${\displaystyle q_{n}\in Q_{n}}$ for ${\displaystyle D+1\leq n\leq N}$. Note that the re-indexing depends on the point.^[17] More succinctly, the Shapley–Folkman lemma states that

${\displaystyle \mathrm {Conv} (\sum _{n=1}^{N}Q_{n})\subseteq \bigcup _{I\subseteq \{1,2,\ldots N\}:~|I|=D}\sum _{n\in I}\mathrm {Conv} (Q_{n})+\sum _{n\notin I}Q_{n}.}$

As an example, every point in ${\displaystyle [0,2]=[0,1]+[0,1]=\mathrm {Conv} (\{0,1\})+\mathrm {Conv} (\{0,1\})}$ is according to the lemma the sum of an element in ${\displaystyle \{0,1\}}$ and an element in ${\displaystyle [0,1]}$.^[8]

Dimension of a real vector space[]

Conversely, the Shapley–Folkman lemma characterizes the dimension of finite-dimensional, real vector spaces. That is, if a vector space obeys the Shapley–Folkman lemma for a natural number D, and for no number less than D, then its dimension is exactly D;^[18] the Shapley–Folkman lemma holds for only finite-dimensional vector spaces.^[19]

Shapley–Folkman theorem and Starr's corollary[]

The circumradius (blue) and inner radius (green) of a point set (dark red, with its convex hull shown as the lighter red dashed lines). The inner radius is smaller than the circumradius except for subsets of a single circle, for which they are equal.

Shapley and Folkman used their lemma to prove their theorem, which bounds the distance between a Minkowski sum and its convex hull, the "convexified" sum:

• The Shapley–Folkman theorem states that the squared Euclidean distance from any point in the convexified sum Conv( Σ Q_n ) to the original (unconvexified) sum Σ Q_n is bounded by the sum of the squares of the D largest circumradii of the sets Q_n (the radii of the smallest spheres enclosing these sets).^[20] This bound is independent of the number of summand-sets N (if N > D).^[21]

The Shapley–Folkman theorem states a bound on the distance between the Minkowski sum and its convex hull; this distance is zero if and only if the sum is convex. Their bound on the distance depends on the dimension D and on the shapes of the summand-sets, but not on the number of summand-sets N, when N > D.^[3]

The circumradius often exceeds (and cannot be less than) the inner radius:^[22]

• The inner radius of a set Q_n is defined to be the smallest number r such that, for any point q in the convex hull of Q_n, there is a sphere of radius r that contains a subset of Q_n whose convex hull contains q.

Starr used the inner radius to reduce the upper bound stated in the Shapley–Folkman theorem:

• Starr's corollary to the Shapley–Folkman theorem states that the squared Euclidean distance from any point x in the convexified sum Conv( Σ Q_n ) to the original (unconvexified) sum Σ Q_n is bounded by the sum of the squares of the D largest inner-radii of the sets Q_n.^[22][23]

Starr's corollary states an upper bound on the Euclidean distance between the Minkowski sum of N sets and the convex hull of the Minkowski sum; this distance between the sum and its convex hull is a measurement of the non-convexity of the set. For simplicity, this distance is called the "non-convexity" of the set (with respect to Starr's measurement). Thus, Starr's bound on the non-convexity of the sum depends on only the D largest inner radii of the summand-sets; however, Starr's bound does not depend on the number of summand-sets N, when N > D. For example, the distance between the convex interval [0, 2] and the non-convex set {0, 1, 2} equals one-half

1/2 = |1 − 1/2| = |0 − 1/2| = |2 − 3/2| = |1 − 3/2|.

Thus, Starr's bound on the non-convexity of the average

1⁄N Σ Q_n

decreases as the number of summands N increases. For example, the distance between the averaged set

1/2 ( {0, 1} + {0, 1} ) = {0, 1/2, 1}

and its convex hull [0, 1] is only 1/4, which is half the distance (1/2) between its summand {0, 1} and [0, 1]. The shapes of a subcollection of only D summand-sets determine the bound on the distance between the average set and its convex hull; thus, as the number of summands increases to infinity, the bound decreases to zero (for summand-sets of uniformly bounded size).^[3] In fact, Starr's bound on the non-convexity of this average set decreases to zero as the number of summands N increases to infinity (when the inner radii of all the summands are bounded by the same number).^[3]

Proofs and computations[]

The original proof of the Shapley–Folkman lemma established only the existence of the representation, but did not provide an algorithm for computing the representation: Similar proofs have been given by Arrow and Hahn,^[24] Cassels,^[25] and Schneider,^[26] among others. An abstract and elegant proof by Ekeland has been extended by Artstein.^[27][28] Different proofs have appeared in unpublished papers, also.^[2][29] In 1981, Starr published an iterative method for computing a representation of a given sum-point; however, his computational proof provides a weaker bound than does the original result.^[30] An elementary proof of the Shapley–Folkman lemma in finite-dimensional space can be found in the book by Bertsekas^[31] together with applications in estimating the duality gap in separable optimization problems and zero-sum games.

Applications[]

The Shapley–Folkman lemma enables researchers to extend results for Minkowski sums of convex sets to sums of general sets, which need not be convex. Such sums of sets arise in economics, in mathematical optimization, and in probability theory; in each of these three mathematical sciences, non-convexity is an important feature of applications.

Economics[]

The consumer prefers every basket of goods on the indifference curve I₃ over each basket on  I₂. The basket (Q_x, Q_y), where the budget line (shown in blue) supports I₂, is optimal and also feasible, unlike any basket lying on  I₃ which is preferred but unfeasible.

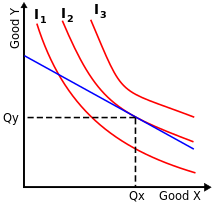
In economics, a consumer's preferences are defined over all "baskets" of goods. Each basket is represented as a non-negative vector, whose coordinates represent the quantities of the goods. On this set of baskets, an indifference curve is defined for each consumer; a consumer's indifference curve contains all the baskets of commodities that the consumer regards as equivalent: That is, for every pair of baskets on the same indifference curve, the consumer does not prefer one basket over another. Through each basket of commodities passes one indifference curve. A consumer's preference set (relative to an indifference curve) is the union of the indifference curve and all the commodity baskets that the consumer prefers over the indifference curve. A consumer's preferences are convex if all such preference sets are convex.^[32]

An optimal basket of goods occurs where the budget-line supports a consumer's preference set, as shown in the diagram. This means that an optimal basket is on the highest possible indifference curve given the budget-line, which is defined in terms of a price vector and the consumer's income (endowment vector). Thus, the set of optimal baskets is a function of the prices, and this function is called the consumer's demand. If the preference set is convex, then at every price the consumer's demand is a convex set, for example, a unique optimal basket or a line-segment of baskets.^[33]

Non-convex preferences[]

When the consumer's preferences have concavities, the consumer may jump between two separate optimal baskets.

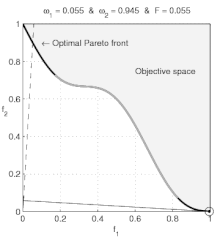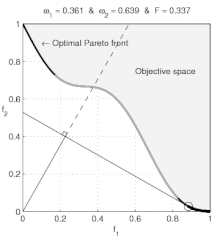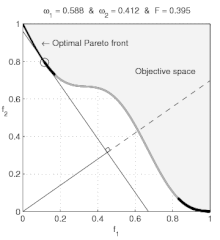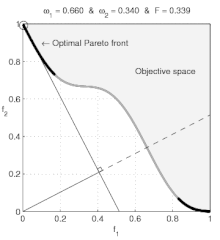
However, if a preference set is non-convex, then some prices determine a budget-line that supports two separate optimal-baskets. For example, we can imagine that, for zoos, a lion costs as much as an eagle, and further that a zoo's budget suffices for one eagle or one lion. We can suppose also that a zoo-keeper views either animal as equally valuable. In this case, the zoo would purchase either one lion or one eagle. Of course, a contemporary zoo-keeper does not want to purchase half of an eagle and half of a lion (or a griffin)! Thus, the zoo-keeper's preferences are non-convex: The zoo-keeper prefers having either animal to having any strictly convex combination of both.^[34]

When the consumer's preference set is non-convex, then (for some prices) the consumer's demand is not connected; a disconnected demand implies some discontinuous behavior by the consumer, as discussed by Harold Hotelling:

If indifference curves for purchases be thought of as possessing a wavy character, convex to the origin in some regions and concave in others, we are forced to the conclusion that it is only the portions convex to the origin that can be regarded as possessing any importance, since the others are essentially unobservable. They can be detected only by the discontinuities that may occur in demand with variation in price-ratios, leading to an abrupt jumping of a point of tangency across a chasm when the straight line is rotated. But, while such discontinuities may reveal the existence of chasms, they can never measure their depth. The concave portions of the indifference curves and their many-dimensional generalizations, if they exist, must forever remain in unmeasurable obscurity.^[35]

The difficulties of studying non-convex preferences were emphasized by Herman Wold^[36] and again by Paul Samuelson, who wrote that non-convexities are "shrouded in eternal darkness ...",^[37] according to Diewert.^[38]

Nonetheless, non-convex preferences were illuminated from 1959 to 1961 by a sequence of papers in The Journal of Political Economy (JPE). The main contributors were Farrell,^[39] Bator,^[40] Koopmans,^[41] and Rothenberg.^[42] In particular, Rothenberg's paper discussed the approximate convexity of sums of non-convex sets.^[43] These JPE-papers stimulated a paper by Lloyd Shapley and Martin Shubik, which considered convexified consumer-preferences and introduced the concept of an "approximate equilibrium".^[44] The JPE-papers and the Shapley–Shubik paper influenced another notion of "quasi-equilibria", due to Robert Aumann.^[45][46]

Starr's 1969 paper and contemporary economics[]

Kenneth Arrow (1972 Nobel laureate) helped Ross M. Starr to study non-convex economies.^[47]

Previous publications on non-convexity and economics were collected in an annotated bibliography by Kenneth Arrow. He gave the bibliography to Starr, who was then an undergraduate enrolled in Arrow's (graduate) advanced mathematical-economics course.^[47] In his term-paper, Starr studied the general equilibria of an artificial economy in which non-convex preferences were replaced by their convex hulls. In the convexified economy, at each price, the aggregate demand was the sum of convex hulls of the consumers' demands. Starr's ideas interested the mathematicians Lloyd Shapley and Jon Folkman, who proved their eponymous lemma and theorem in "private correspondence", which was reported by Starr's published paper of 1969.^[1]

In his 1969 publication, Starr applied the Shapley–Folkman–Starr theorem. Starr proved that the "convexified" economy has general equilibria that can be closely approximated by "quasi-equilibria" of the original economy, when the number of agents exceeds the dimension of the goods: Concretely, Starr proved that there exists at least one quasi-equilibrium of prices p_opt with the following properties:

• For each quasi-equilibrium's prices p_opt, all consumers can choose optimal baskets (maximally preferred and meeting their budget constraints).
• At quasi-equilibrium prices p_opt in the convexified economy, every good's market is in equilibrium: Its supply equals its demand.
• For each quasi-equilibrium, the prices "nearly clear" the markets for the original economy: an upper bound on the distance between the set of equilibria of the "convexified" economy and the set of quasi-equilibria of the original economy followed from Starr's corollary to the Shapley–Folkman theorem.^[48]

Starr established that

"in the aggregate, the discrepancy between an allocation in the fictitious economy generated by [taking the convex hulls of all of the consumption and production sets] and some allocation in the real economy is bounded in a way that is independent of the number of economic agents. Therefore, the average agent experiences a deviation from intended actions that vanishes in significance as the number of agents goes to infinity".^[49]

Following Starr's 1969 paper, the Shapley–Folkman–Starr results have been widely used in economic theory. Roger Guesnerie summarized their economic implications: "Some key results obtained under the convexity assumption remain (approximately) relevant in circumstances where convexity fails. For example, in economies with a large consumption side, preference nonconvexities do not destroy the standard results".^[50] "The derivation of these results in general form has been one of the major achievements of postwar economic theory", wrote Guesnerie.^[4] The topic of non-convex sets in economics has been studied by many Nobel laureates: Arrow (1972), Robert Aumann (2005), Gérard Debreu (1983), Tjalling Koopmans (1975), Paul Krugman (2008), and Paul Samuelson (1970); the complementary topic of convex sets in economics has been emphasized by these laureates, along with Leonid Hurwicz, Leonid Kantorovich (1975), and Robert Solow (1987).^[51] The Shapley–Folkman–Starr results have been featured in the economics literature: in microeconomics,^[52] in general-equilibrium theory,^[53][54] in public economics^[55] (including market failures),^[56] as well as in game theory,^[57] in mathematical economics,^[58] and in applied mathematics (for economists).^[59][60] The Shapley–Folkman–Starr results have also influenced economics research using measure and integration theory.^[61]

Mathematical optimization[]

A function is convex if the region above its graph is a convex set.

The Shapley–Folkman lemma has been used to explain why large minimization problems with non-convexities can be nearly solved (with iterative methods whose convergence proofs are stated for only convex problems). The Shapley–Folkman lemma has encouraged the use of methods of convex minimization on other applications with sums of many functions.^[62]

Preliminaries of optimization theory[]

Nonlinear optimization relies on the following definitions for functions:

• The graph of a function f is the set of the pairs of arguments x and function evaluations f(x)

Graph(f) = { (x, f(x) ) }

• The epigraph of a real-valued function f is the set of points above the graph

The sine function is non-convex.

Epi(f) = { (x, u) : f(x) ≤ u }.

• A real-valued function is defined to be a convex function if its epigraph is a convex set.^[63]

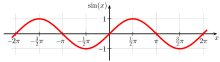
For example, the quadratic function f(x) = x² is convex, as is the absolute value function g(x) = |x|. However, the sine function (pictured) is non-convex on the interval (0, π).

Additive optimization problems[]

In many optimization problems, the objective function f is separable: that is, f is the sum of many summand-functions, each of which has its own argument:

f(x) = f( (x₁, ..., x_N) ) = Σ f_n(x_n).

For example, problems of linear optimization are separable. Given a separable problem with an optimal solution, we fix an optimal solution

x_min = (x₁, ..., x_N)_min

with the minimum value f(x_min). For this separable problem, we also consider an optimal solution (x_min, f(x_min) ) to the "convexified problem", where convex hulls are taken of the graphs of the summand functions. Such an optimal solution is the limit of a sequence of points in the convexified problem

(x_j, f(x_j) ) ∈  Σ Conv (Graph( f_n ) ).^[5][64]

Of course, the given optimal-point is a sum of points in the graphs of the original summands and of a small number of convexified summands, by the Shapley–Folkman lemma.

This analysis was published by Ivar Ekeland in 1974 to explain the apparent convexity of separable problems with many summands, despite the non-convexity of the summand problems. In 1973, the young mathematician Claude Lemaréchal was surprised by his success with convex minimization methods on problems that were known to be non-convex; for minimizing nonlinear problems, a solution of the dual problem need not provide useful information for solving the primal problem, unless the primal problem be convex and satisfy a constraint qualification. Lemaréchal's problem was additively separable, and each summand function was non-convex; nonetheless, a solution to the dual problem provided a close approximation to the primal problem's optimal value.^[65][5][66] Ekeland's analysis explained the success of methods of convex minimization on large and separable problems, despite the non-convexities of the summand functions. Ekeland and later authors argued that additive separability produced an approximately convex aggregate problem, even though the summand functions were non-convex. The crucial step in these publications is the use of the Shapley–Folkman lemma.^[5][66][67] The Shapley–Folkman lemma has encouraged the use of methods of convex minimization on other applications with sums of many functions.^{[5][6][59][62]}

Probability and measure theory[]

Convex sets are often studied with probability theory. Each point in the convex hull of a (non-empty) subset Q of a finite-dimensional space is the expected value of a simple random vector that takes its values in Q, as a consequence of Carathéodory's lemma. Thus, for a non-empty set Q, the collection of the expected values of the simple, Q-valued random vectors equals Q's convex hull; this equality implies that the Shapley–Folkman–Starr results are useful in probability theory.^[68] In the other direction, probability theory provides tools to examine convex sets generally and the Shapley–Folkman–Starr results specifically.^[69] The Shapley–Folkman–Starr results have been widely used in the probabilistic theory of random sets,^[70] for example, to prove a law of large numbers,^[7][71] a central limit theorem,^[71][72] and a large-deviations principle.^[73] These proofs of probabilistic limit theorems used the Shapley–Folkman–Starr results to avoid the assumption that all the random sets be convex.

A probability measure is a finite measure, and the Shapley–Folkman lemma has applications in non-probabilistic measure theory, such as the theories of volume and of vector measures. The Shapley–Folkman lemma enables a refinement of the Brunn–Minkowski inequality, which bounds the volume of sums in terms of the volumes of their summand-sets.^[74] The volume of a set is defined in terms of the Lebesgue measure, which is defined on subsets of Euclidean space. In advanced measure-theory, the Shapley–Folkman lemma has been used to prove Lyapunov's theorem, which states that the range of a vector measure is convex.^[75] Here, the traditional term "range" (alternatively, "image") is the set of values produced by the function. A vector measure is a vector-valued generalization of a measure; for example, if p₁ and p₂ are probability measures defined on the same measurable space, then the product function p₁ p₂ is a vector measure, where p₁ p₂ is defined for every event ω by

(p₁ p₂)(ω)=(p₁(ω), p₂(ω)).

Lyapunov's theorem has been used in economics,^[45][76] in ("bang-bang") control theory, and in statistical theory.^[77] Lyapunov's theorem has been called a continuous counterpart of the Shapley–Folkman lemma,^[3] which has itself been called a discrete analogue of Lyapunov's theorem.^[78]

Notes[]

References[]

• Arrow, Kenneth J.; Hahn, Frank H. (1980) [1971]. General competitive analysis. Advanced Textbooks in Economics. 12 (reprint of San Francisco, CA: Holden-Day, Inc. Mathematical Economics Texts 6 ed.). Amsterdam: North-Holland. ISBN 0-444-85497-5. MR 0439057.
• Artstein, Zvi (1980). "Discrete and continuous bang-bang and facial spaces, or: Look for the extreme points". SIAM Review. 22 (2): 172–185. doi:10.1137/1022026. JSTOR 2029960. MR 0564562.
• Carter, Michael (2001). Foundations of mathematical economics. Cambridge, Mass.: MIT Press. pp. xx+649. ISBN 0-262-53192-5. MR 1865841. (Author's website with answers to exercises). Archived from the original on 15 September 2006.
• Diewert, W. E. (1982). "12 Duality approaches to microeconomic theory". In Arrow, Kenneth Joseph; Intriligator, Michael D (eds.). Handbook of mathematical economics, Volume II. Handbooks in Economics. 1. Amsterdam: North-Holland Publishing Co. pp. 535–599. doi:10.1016/S1573-4382(82)02007-4. ISBN 978-0-444-86127-6. MR 0648778.
• Ekeland, Ivar (1999) [1976]. "Appendix I: An a priori estimate in convex programming". In Ekeland, Ivar; Temam, Roger (eds.). Convex analysis and variational problems. Classics in Applied Mathematics. 28 (Corrected reprinting of the North-Holland ed.). Philadelphia: Society for Industrial and Applied Mathematics (SIAM). pp. 357–373. ISBN 0-89871-450-8. MR 1727362.
• Green, Jerry; Heller, Walter P. (1981). "1 Mathematical analysis and convexity with applications to economics". In Arrow, Kenneth Joseph; Intriligator, Michael D (eds.). Handbook of mathematical economics, Volume I. Handbooks in Economics. 1. Amsterdam: North-Holland Publishing Co. pp. 15–52. doi:10.1016/S1573-4382(81)01005-9. ISBN 0-444-86126-2. MR 0634800.
• Guesnerie, Roger (1989). "First-best allocation of resources with nonconvexities in production". In Cornet, Bernard; Tulkens, Henry (eds.). Contributions to Operations Research and Economics: The twentieth anniversary of CORE (Papers from the symposium held in Louvain-la-Neuve, January 1987). Cambridge, Mass.: MIT Press. pp. 99–143. ISBN 0-262-03149-3. MR 1104662.
• Mas-Colell, A. (1987). "Non-convexity". In Eatwell, John; Milgate, Murray; Newman, Peter (eds.). The new Palgrave: A dictionary of economics (first ed.). Palgrave Macmillan. pp. 653–661. doi:10.1057/9780230226203.3173. ISBN 9780333786765. (PDF file at Mas-Colell's homepage).
• Rockafellar, R. Tyrrell (1997). Convex analysis. Princeton Landmarks in Mathematics. Princeton, N.J.: Princeton University Press. pp. xviii+451. ISBN 0-691-01586-4. MR 1451876.. Reprint of the 1970 (MR274683) Princeton Mathematical Series 28
• Schneider, Rolf (1993). Convex bodies: The Brunn–Minkowski theory. Encyclopedia of Mathematics and its Applications. 44. Cambridge, UK: Cambridge University Press. pp. xiv+490. ISBN 0-521-35220-7. MR 1216521.
• Starr, Ross M. (1969). "Quasi-equilibria in markets with non-convex preferences (Appendix 2: The Shapley–Folkman theorem, pp. 35–37)". Econometrica. 37 (1): 25–38. doi:10.2307/1909201. JSTOR 1909201.
• Starr, Ross M. (2008). "Shapley–Folkman theorem". In Durlauf, Steven N.; Blume, Lawrence E (eds.). The new Palgrave dictionary of economics (Second ed.). Palgrave Macmillan. pp. 317–318 (1st ed.). doi:10.1057/9780230226203.1518. ISBN 978-0-333-78676-5.

External links[]

• Anderson, Robert M. (March 2005). "1 The Shapley–Folkman theorem" (PDF). Economics 201B: Nonconvex preferences and approximate equilibria. Berkeley, Calif.: Economics Department, University of California, Berkeley. pp. 1–5. Retrieved 15 January 2011.
• Howe, Roger (November 1979). On the tendency toward convexity of the vector sum of sets (PDF) (Report). Cowles Foundation discussion papers. 538. New Haven, Conn.: Cowles Foundation for Research in Economics, Yale University. Retrieved 15 January 2011.
• Starr, Ross M. (September 2009). "8 Convex sets, separation theorems, and non-convex sets in R^N (Section 8.2.3 Measuring non-convexity, the Shapley–Folkman theorem)" (PDF). General equilibrium theory: An introduction. pp. 3–6. doi:10.1017/CBO9781139174749. ISBN 9781139174749. MR 1462618. (Draft of second edition, from Starr's course at the Economics Department of the University of California, San Diego).
• Starr, Ross M. (May 2007). "Shapley–Folkman theorem" (PDF). pp. 1–3. (Draft of article for the second edition of New Palgrave Dictionary of Economics). Retrieved 15 January 2011.