Snub dodecahedral prism
| Snub dodecahedral prism | |
|---|---|
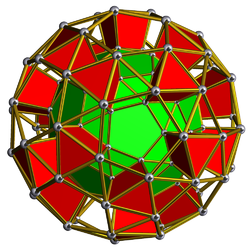 Schlegel diagram | |
| Type | Prismatic uniform polychoron |
| Uniform index | 64 |
| Schläfli symbol | sr{3,5}×{} |
| Coxeter-Dynkin |     
|
| Cells | 94 total: 2  3.3.3.3.5
|
| Faces | 334 total: 160 {3} 150 {4} 24 {5} |
| Edges | 360 |
| Vertices | 120 |
| Vertex figure | 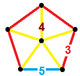 irr. pentagonal pyramid |
| Symmetry group | [(5,3)+,2], order 120 |
| Properties | convex |
In geometry, a snub dodecahedral prism or snub icosidodecahedral prism is a convex uniform polychoron (four-dimensional polytope).
It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes, in this case a pair of snub dodecahedra.
Alternative names[]
- Snub-icosidodecahedral dyadic prism (Norman W. Johnson)
- Sniddip (Jonathan Bowers: for snub-dodecahedral prism)
- Snub-icosidodecahedral hyperprism
- Snub-dodecahedral prism
- Snub-dodecahedral hyperprism
See also[]
- Snub dodecahedral antiprism ht0,1,2,3{5,3,2}, or
- A related nonuniform polychoron
External links[]
- 6. Convex uniform prismatic polychora - Model 64, George Olshevsky.
- Klitzing, Richard. "4D uniform polytopes (polychora) x s3s5s - sniddip".
 | This 4-polytope article is a stub. You can help Wikipedia by . |
Categories:
- 4-polytopes
- 4-polytopes stubs