Snub rhombicuboctahedron

Snub rhombicuboctahedron
Schläfli symbol	srr{4,3} = ${\displaystyle sr{\begin{Bmatrix}4\\3\end{Bmatrix}}}$
Conway notation	saC
Faces	74: 8+48 {3} 6+12 {4}
Edges	120
Vertices	48
Symmetry group	O, [4,3]+, (432) order 24
Dual polyhedron
Properties	convex, chiral

The snub rhombicuboctahedron is a polyhedron, constructed as a truncated rhombicuboctahedron. It has 74 faces: 18 squares, and 56 triangles. It can also be called the Conway snub cuboctahedron in but will be confused with the Coxeter snub cuboctahedron, the snub cube.

Related polyhedra[]

The snub rhombicuboctahedron can be seen in sequence of operations from the cuboctahedron.

Name	Cubocta- hedron	Truncated cubocta- hedron	Snub cubocta- hedron	Truncated rhombi- cubocta- hedron	Snub rhombi- cubocta- hedron
Coxeter	CO (rC)	tCO (trC)	sCO (srC)	trCO (trrC)	srCO (htrrC)
Conway	aC	taC = bC	sC	taaC = baC	saC
Image
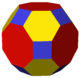
Conway	jC	mC	gC	maC	gaC
Dual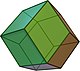

See also[]

• Expanded cuboctahedron
• Truncated rhombicosidodecahedron

References[]

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5

External links[]

• George Hart's Conway interpreter: generates polyhedra in VRML, taking Conway notation as input