Arcsine distribution

Arcsine

Probability density function
Cumulative distribution function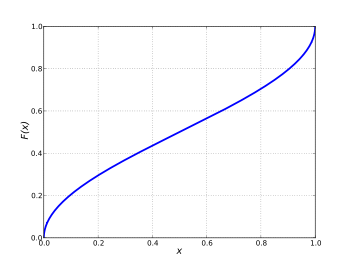
Parameters	none
Support	${\displaystyle x\in [0,1]}$
PDF	${\displaystyle f(x)={\frac {1}{\pi {\sqrt {x(1-x)}}}}}$
CDF	${\displaystyle F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {x}}\right)}$
Mean	${\displaystyle {\frac {1}{2}}}$
Median	${\displaystyle {\frac {1}{2}}}$
Mode	${\displaystyle x\in \{0,1\}}$
Variance	${\displaystyle {\tfrac {1}{8}}}$
Skewness	${\displaystyle 0}$
Ex. kurtosis	${\displaystyle -{\tfrac {3}{2}}}$
Entropy	${\displaystyle \ln {\tfrac {\pi }{4}}}$
MGF	${\displaystyle 1+\sum _{k=1}^{\infty }\left(\prod _{r=0}^{k-1}{\frac {2r+1}{2r+2}}\right){\frac {t^{k}}{k!}}}$
CF	${\displaystyle {}_{1}F_{1}({\tfrac {1}{2}};1;i\,t)\ }$

In probability theory, the arcsine distribution is the probability distribution whose cumulative distribution function is

${\displaystyle F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {x}}\right)={\frac {\arcsin(2x-1)}{\pi }}+{\frac {1}{2}}}$

for 0 ≤ x ≤ 1, and whose probability density function is

${\displaystyle f(x)={\frac {1}{\pi {\sqrt {x(1-x)}}}}}$

on (0, 1). The standard arcsine distribution is a special case of the beta distribution with α = β = 1/2. That is, if ${\displaystyle X}$ is an arcsine-distributed random variable, then ${\displaystyle X\sim {\rm {Beta}}{\bigl (}{\tfrac {1}{2}},{\tfrac {1}{2}}{\bigr )}}$. By extension, the arcsine distribution is a special case of the Pearson type I distribution.

The arcsine distribution appears in the Lévy arcsine law, in the Erdős arcsine law, and as the Jeffreys prior for the probability of success of a Bernoulli trial.^{[1] [2]}

Generalization[]

Arcsine – bounded support

Parameters	${\displaystyle -\infty <a<b<\infty \,}$
Support	${\displaystyle x\in [a,b]}$
PDF	${\displaystyle f(x)={\frac {1}{\pi {\sqrt {(x-a)(b-x)}}}}}$
CDF	${\displaystyle F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {\frac {x-a}{b-a}}}\right)}$
Mean	${\displaystyle {\frac {a+b}{2}}}$
Median	${\displaystyle {\frac {a+b}{2}}}$
Mode	${\displaystyle x\in {a,b}}$
Variance	${\displaystyle {\tfrac {1}{8}}(b-a)^{2}}$
Skewness	${\displaystyle 0}$
Ex. kurtosis	${\displaystyle -{\tfrac {3}{2}}}$

Arbitrary bounded support[]

The distribution can be expanded to include any bounded support from a ≤ x ≤ b by a simple transformation

${\displaystyle F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {\frac {x-a}{b-a}}}\right)}$

for a ≤ x ≤ b, and whose probability density function is

${\displaystyle f(x)={\frac {1}{\pi {\sqrt {(x-a)(b-x)}}}}}$

on (a, b).

Shape factor[]

The generalized standard arcsine distribution on (0,1) with probability density function

${\displaystyle f(x;\alpha )={\frac {\sin \pi \alpha }{\pi }}x^{-\alpha }(1-x)^{\alpha -1}}$

is also a special case of the beta distribution with parameters ${\displaystyle {\rm {Beta}}(1-\alpha ,\alpha )}$.

Note that when ${\displaystyle \alpha ={\tfrac {1}{2}}}$ the general arcsine distribution reduces to the standard distribution listed above.

Properties[]

• Arcsine distribution is closed under translation and scaling by a positive factor
  • If ${\displaystyle X\sim {\rm {Arcsine}}(a,b)\ {\text{then }}kX+c\sim {\rm {Arcsine}}(ak+c,bk+c)}$
• The square of an arcsine distribution over (-1, 1) has arcsine distribution over (0, 1)
  • If ${\displaystyle X\sim {\rm {Arcsine}}(-1,1)\ {\text{then }}X^{2}\sim {\rm {Arcsine}}(0,1)}$

Characteristic function[]

The characteristic function of the arcsine distribution is a confluent hypergeometric function and given as ${\displaystyle {}_{1}F_{1}({\tfrac {1}{2}};1;i\,t)\ }$.

The arcsine distribution has an application to beamforming and pattern synthesis in reference: https://ieeexplore.ieee.org/abstract/document/8170756/

Related distributions[]

• If U and V are i.i.d uniform (−π,π) random variables, then ${\displaystyle \sin(U)}$, ${\displaystyle \sin(2U)}$, ${\displaystyle -\cos(2U)}$, ${\displaystyle \sin(U+V)}$ and ${\displaystyle \sin(U-V)}$ all have an ${\displaystyle {\rm {Arcsine}}(-1,1)}$ distribution.
• If ${\displaystyle X}$ is the generalized arcsine distribution with shape parameter ${\displaystyle \alpha }$ supported on the finite interval [a,b] then ${\displaystyle {\frac {X-a}{b-a}}\sim {\rm {Beta}}(1-\alpha ,\alpha )\ }$
• If X ~ Cauchy(0, 1) then ${\displaystyle {\tfrac {1}{1+X^{2}}}}$ has a standard arcsine distribution

Application[]

The ArcSine distribution has an application to beamforming and pattern synthesis provided in reference https://ieeexplore.ieee.org/document/8170756 ^[3]

See also[]

• Arcsine

References[]

• Rogozin, B.A. (2001) [1994], "Arcsine distribution", Encyclopedia of Mathematics, EMS Press