Beltrami identity

Eugenio Beltrami

The Beltrami identity, named after Eugenio Beltrami, is a special case of the Euler–Lagrange equation in the calculus of variations.

The Euler–Lagrange equation serves to extremize action functionals of the form

${\displaystyle I[u]=\int _{a}^{b}L[x,u(x),u'(x)]\,dx\,,}$

where ${\displaystyle a}$ and ${\displaystyle b}$ are constants and ${\displaystyle u'(x)={\frac {du}{dx}}}$.^[1]

If ${\displaystyle {\frac {\partial L}{\partial x}}=0}$, then the Euler–Lagrange equation reduces to the Beltrami identity,

where C is a constant.^{[2][note 1]}

Derivation[]

The following derivation of the Beltrami identity starts with the Euler–Lagrange equation,

${\displaystyle {\frac {\partial L}{\partial u}}={\frac {d}{dx}}{\frac {\partial L}{\partial u'}}\,.}$

Multiplying both sides by u′,

${\displaystyle u'{\frac {\partial L}{\partial u}}=u'{\frac {d}{dx}}{\frac {\partial L}{\partial u'}}\,.}$

According to the chain rule,

${\displaystyle {dL \over dx}={\partial L \over \partial u}u'+{\partial L \over \partial u'}u''+{\partial L \over \partial x}\,,}$

where ${\displaystyle u''={\frac {du'}{dx}}={\frac {d^{2}u}{dx^{2}}}}$.

Rearranging the expression above yields,

${\displaystyle u'{\partial L \over \partial u}={dL \over dx}-{\partial L \over \partial u'}u''-{\partial L \over \partial x}\,.}$

Thus, substituting this expression for ${\displaystyle u'{\frac {\partial L}{\partial u}}}$into the second equation of this derivation and moving all terms to one side,

${\displaystyle {dL \over dx}-{\partial L \over \partial u'}u''-{\partial L \over \partial x}-u'{\frac {d}{dx}}{\frac {\partial L}{\partial u'}}=0\,.}$

By the product rule, the last term is re-expressed as

${\displaystyle u'{\frac {d}{dx}}{\frac {\partial L}{\partial u'}}={\frac {d}{dx}}\left({\frac {\partial L}{\partial u'}}u'\right)-{\frac {\partial L}{\partial u'}}u''\,,}$

and rearranging,

${\displaystyle {d \over dx}\left({L-u'{\frac {\partial L}{\partial u'}}}\right)={\partial L \over \partial x}\,.}$

For the case of ${\displaystyle {\frac {\partial L}{\partial x}}=0}$, this reduces to

${\displaystyle {d \over dx}\left({L-u'{\frac {\partial L}{\partial u'}}}\right)=0\,,}$

so that taking the antiderivative results in the Beltrami identity,

${\displaystyle L-u'{\frac {\partial L}{\partial u'}}=C\,,}$

where C is a constant.^[3]

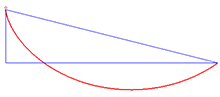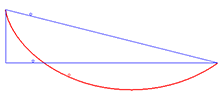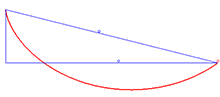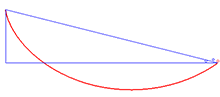
Applications[]

Solution to the brachistochrone problem[]

The solution to the brachistochrone problem is the cycloid.

An example of an application of the Beltrami identity is the brachistochrone problem, which involves finding the curve ${\displaystyle y=y(x)}$ that minimizes the integral

${\displaystyle I[y]=\int _{0}^{a}{\sqrt {{1+y'^{\,2}} \over y}}dx\,.}$

The integrand

${\displaystyle L(y,y')={\sqrt {{1+y'^{\,2}} \over y}}}$

does not depend explicitly on the variable of integration ${\displaystyle x}$, so the Beltrami identity applies,

${\displaystyle L-y'{\frac {\partial L}{\partial y'}}=C\,.}$

Substituting for ${\displaystyle L}$ and simplifying,

${\displaystyle y(1+y'^{\,2})=1/C^{2}~~{\text{(constant)}}\,,}$

which can be solved with the result put in the form of parametric equations

${\displaystyle x=A(\phi -\sin \phi )}$

${\displaystyle y=A(1-\cos \phi )}$

with ${\displaystyle A}$ being half the above constant, ${\displaystyle {\frac {1}{2C^{2}}}}$, and ${\displaystyle \phi }$ being a variable. These are the parametric equations for a cycloid.^[4]

Notes[]

References[]