Omnitruncated simplectic honeycomb

In geometry an omnitruncated simplectic honeycomb or omnitruncated n-simplex honeycomb is an n-dimensional uniform tessellation, based on the symmetry of the ${\displaystyle {\tilde {A}}_{n}}$ affine Coxeter group. Each is composed of omnitruncated simplex facets. The vertex figure for each is an irregular n-simplex.

The facets of an omnitruncated simplectic honeycomb are called permutahedra and can be positioned in n+1 space with integral coordinates, permutations of the whole numbers (0,1,..,n).

n	${\displaystyle {\tilde {A}}_{1+}}$	Image	Tessellation	Facets	Vertex figure	Facets per vertex figure	Vertices per vertex figure
1	${\displaystyle {\tilde {A}}_{1}}$		Apeirogon	Line segment	Line segment	1	2
2	${\displaystyle {\tilde {A}}_{2}}$		Hexagonal tiling	hexagon	Equilateral triangle	3 hexagons	3
3	${\displaystyle {\tilde {A}}_{3}}$		Bitruncated cubic honeycomb	Truncated octahedron	irr. tetrahedron	4 truncated octahedron	4
4	${\displaystyle {\tilde {A}}_{4}}$		Omnitruncated 4-simplex honeycomb	Omnitruncated 4-simplex	irr. 5-cell	5 omnitruncated 4-simplex	5
5	${\displaystyle {\tilde {A}}_{5}}$		Omnitruncated 5-simplex honeycomb	Omnitruncated 5-simplex	irr. 5-simplex	6 omnitruncated 5-simplex	6
6	${\displaystyle {\tilde {A}}_{6}}$		Omnitruncated 6-simplex honeycomb	Omnitruncated 6-simplex	irr. 6-simplex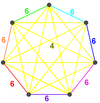	7 omnitruncated 6-simplex	7
7	${\displaystyle {\tilde {A}}_{7}}$		Omnitruncated 7-simplex honeycomb	Omnitruncated 7-simplex	irr. 7-simplex	8 omnitruncated 7-simplex	8
8	${\displaystyle {\tilde {A}}_{8}}$		Omnitruncated 8-simplex honeycomb	Omnitruncated 8-simplex	irr. 8-simplex	9 omnitruncated 8-simplex	9

Projection by folding[]

The (2n-1)-simplex honeycombs can be projected into the n-dimensional omnitruncated hypercubic honeycomb by a geometric folding operation that maps two pairs of mirrors into each other, sharing the same vertex arrangement:

${\displaystyle {\tilde {A}}_{3}}$		${\displaystyle {\tilde {A}}_{5}}$		${\displaystyle {\tilde {A}}_{7}}$		${\displaystyle {\tilde {A}}_{9}}$		...
${\displaystyle {\tilde {C}}_{2}}$		${\displaystyle {\tilde {C}}_{3}}$		${\displaystyle {\tilde {C}}_{4}}$		${\displaystyle {\tilde {C}}_{5}}$		...

See also[]

• Hypercubic honeycomb
• Alternated hypercubic honeycomb
• Quarter hypercubic honeycomb
• Simplectic honeycomb
• Truncated simplectic honeycomb

References[]

• George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
• Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
• Norman Johnson Uniform Polytopes, Manuscript (1991)
• Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]

v t Fundamental convex regular and uniform honeycombs in dimensions 2–9
Space	Family	${\displaystyle {\tilde {A}}_{n-1}}$	${\displaystyle {\tilde {C}}_{n-1}}$	${\displaystyle {\tilde {B}}_{n-1}}$	${\displaystyle {\tilde {D}}_{n-1}}$	${\displaystyle {\tilde {G}}_{2}}$ / ${\displaystyle {\tilde {F}}_{4}}$ / ${\displaystyle {\tilde {E}}_{n-1}}$
E2	Uniform tiling	{3[3]}	δ3	hδ3	qδ3	Hexagonal
E3	Uniform convex honeycomb	{3[4]}	δ4	hδ4	qδ4
E4	Uniform 4-honeycomb	{3[5]}	δ5	hδ5	qδ5	24-cell honeycomb
E5	Uniform 5-honeycomb	{3[6]}	δ6	hδ6	qδ6
E6	Uniform 6-honeycomb	{3[7]}	δ7	hδ7	qδ7	222
E7	Uniform 7-honeycomb	{3[8]}	δ8	hδ8	qδ8	133 • 331
E8	Uniform 8-honeycomb	{3[9]}	δ9	hδ9	qδ9	152 • 251 • 521
E9	Uniform 9-honeycomb	{3[10]}	δ10	hδ10	qδ10
E10	Uniform 10-honeycomb	{3[11]}	δ11	hδ11	qδ11
En-1	Uniform (n-1)-honeycomb	{3[n]}	δn	hδn	qδn	1k2 • 2k1 • k21