Quarter hypercubic honeycomb

In geometry, the quarter hypercubic honeycomb (or quarter n-cubic honeycomb) is a dimensional infinite series of honeycombs, based on the hypercube honeycomb. It is given a Schläfli symbol q{4,3...3,4} or Coxeter symbol qδ₄ representing the regular form with three quarters of the vertices removed and containing the symmetry of Coxeter group ${\displaystyle {\tilde {D}}_{n-1}}$ for n ≥ 5, with ${\displaystyle {\tilde {D}}_{4}}$ = ${\displaystyle {\tilde {A}}_{4}}$ and for quarter n-cubic honeycombs ${\displaystyle {\tilde {D}}_{5}}$ = ${\displaystyle {\tilde {B}}_{5}}$.^[1]

qδn	Name	Schläfli symbol	Coxeter diagrams	Facets			Vertex figure
qδ3	quarter square tiling	q{4,4}	or or	h{4}={2}	{ }×{ }		{ }×{ }
qδ4	quarter cubic honeycomb	q{4,3,4}	or or	h{4,3}	h2{4,3}		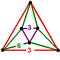Elongated triangular antiprism
qδ5	quarter tesseractic honeycomb	q{4,32,4}	or or	h{4,32}	h3{4,32}		{3,4}×{}
qδ6	quarter 5-cubic honeycomb	q{4,33,4}		h{4,33}	h4{4,33}		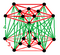Rectified 5-cell antiprism
qδ7	quarter 6-cubic honeycomb	q{4,34,4}		h{4,34}	h5{4,34}	{3,3}×{3,3}
qδ8	quarter 7-cubic honeycomb	q{4,35,4}		h{4,35}	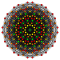h6{4,35}	{3,3}×{3,31,1}
qδ9	quarter 8-cubic honeycomb	q{4,36,4}		h{4,36}		{3,3}×{3,32,1} {3,31,1}×{3,31,1}
qδn	quarter n-cubic honeycomb	q{4,3n-3,4}	...	h{4,3n-2}	hn-2{4,3n-2}	...

See also[]

• Hypercubic honeycomb
• Alternated hypercubic honeycomb
• Simplectic honeycomb
• Truncated simplectic honeycomb
• Omnitruncated simplectic honeycomb

References[]

• Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
  1. pp. 122–123, 1973. (The lattice of hypercubes γ_n form the cubic honeycombs, δ_n+1)
  2. pp. 154–156: Partial truncation or alternation, represented by q prefix
  3. p. 296, Table II: Regular honeycombs, δ_n+1
• Kaleidoscopes: Selected Writings of H. S. M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45] See p318 [2]
• Klitzing, Richard. "1D-8D Euclidean tesselations".

v t Fundamental convex regular and uniform honeycombs in dimensions 2–9
Space	Family	${\displaystyle {\tilde {A}}_{n-1}}$	${\displaystyle {\tilde {C}}_{n-1}}$	${\displaystyle {\tilde {B}}_{n-1}}$	${\displaystyle {\tilde {D}}_{n-1}}$	${\displaystyle {\tilde {G}}_{2}}$ / ${\displaystyle {\tilde {F}}_{4}}$ / ${\displaystyle {\tilde {E}}_{n-1}}$
E2	Uniform tiling	{3[3]}	δ3	hδ3	qδ3	Hexagonal
E3	Uniform convex honeycomb	{3[4]}	δ4	hδ4	qδ4
E4	Uniform 4-honeycomb	{3[5]}	δ5	hδ5	qδ5	24-cell honeycomb
E5	Uniform 5-honeycomb	{3[6]}	δ6	hδ6	qδ6
E6	Uniform 6-honeycomb	{3[7]}	δ7	hδ7	qδ7	222
E7	Uniform 7-honeycomb	{3[8]}	δ8	hδ8	qδ8	133 • 331
E8	Uniform 8-honeycomb	{3[9]}	δ9	hδ9	qδ9	152 • 251 • 521
E9	Uniform 9-honeycomb	{3[10]}	δ10	hδ10	qδ10
E10	Uniform 10-honeycomb	{3[11]}	δ11	hδ11	qδ11
En-1	Uniform (n-1)-honeycomb	{3[n]}	δn	hδn	qδn	1k2 • 2k1 • k21