6-demicube
| Demihexeract (6-demicube) | ||
|---|---|---|
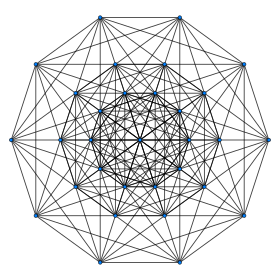 Petrie polygon projection | ||
| Type | Uniform 6-polytope | |
| Family | demihypercube | |
| Schläfli symbol | {3,33,1} = h{4,34} s{21,1,1,1,1} | |
| Coxeter diagrams |
| |
| Coxeter symbol | 131 | |
| 5-faces | 44 | 12 {31,2,1} 32 {34} |
| 4-faces | 252 | 60 {31,1,1} 192 {33} |
| Cells | 640 | 160 {31,0,1} 480 {3,3} |
| Faces | 640 | {3} |
| Edges | 240 | |
| Vertices | 32 | |
| Vertex figure | Rectified 5-simplex | |
| Symmetry group | D6, [33,1,1] = [1+,4,34] [25]+ | |
| Petrie polygon | decagon | |
| Properties | convex | |
In geometry, a 6-demicube or demihexteract is a uniform 6-polytope, constructed from a 6-cube (hexeract) with alternated vertices removed. It is part of a dimensionally infinite family of uniform polytopes called demihypercubes.
E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as HM6 for a 6-dimensional half measure polytope.
Coxeter named this polytope as 131 from its Coxeter diagram, with a ring on one of the 1-length branches, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . It can named similarly by a 3-dimensional exponential Schläfli symbol or {3,33,1}.
. It can named similarly by a 3-dimensional exponential Schläfli symbol or {3,33,1}.
Cartesian coordinates[]
Cartesian coordinates for the vertices of a demihexeract centered at the origin are alternate halves of the hexeract:
- (±1,±1,±1,±1,±1,±1)
with an odd number of plus signs.
As a configuration[]
This configuration matrix represents the 6-demicube. The rows and columns correspond to vertices, edges, faces, cells, 4-faces and 5-faces. The diagonal numbers say how many of each element occur in the whole 6-demicube. The nondiagonal numbers say how many of the column's element occur in or at the row's element.[1][2]
The diagonal f-vector numbers are derived through the Wythoff construction, dividing the full group order of a subgroup order by removing one mirror at a time.[3]
| D6 | k-face | fk | f0 | f1 | f2 | f3 | f4 | f5 | k-figure | notes | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A4 | ( ) | f0 | 32 | 15 | 60 | 20 | 60 | 15 | 30 | 6 | 6 | r{3,3,3,3} | D6/A4 = 32*6!/5! = 32 | |
| A3A1A1 | { } | f1 | 2 | 240 | 8 | 4 | 12 | 6 | 8 | 4 | 2 | {}x{3,3} | D6/A3A1A1 = 32*6!/4!/2/2 = 240 | |
| A3A2 | {3} | f2 | 3 | 3 | 640 | 1 | 3 | 3 | 3 | 3 | 1 | {3}v( ) | D6/A3A2 = 32*6!/4!/3! = 640 | |
| A3A1 | h{4,3} | f3 | 4 | 6 | 4 | 160 | * | 3 | 0 | 3 | 0 | {3} | D6/A3A1 = 32*6!/4!/2 = 160 | |
| A3A2 | {3,3} | 4 | 6 | 4 | * | 480 | 1 | 2 | 2 | 1 | {}v( ) | D6/A3A2 = 32*6!/4!/3! = 480 | ||
| D4A1 | h{4,3,3} | f4 | 8 | 24 | 32 | 8 | 8 | 60 | * | 2 | 0 | { } | D6/D4A1 = 32*6!/8/4!/2 = 60 | |
| A4 | {3,3,3} | 5 | 10 | 10 | 0 | 5 | * | 192 | 1 | 1 | D6/A4 = 32*6!/5! = 192 | |||
| D5 | h{4,3,3,3} | f5 | 16 | 80 | 160 | 40 | 80 | 10 | 16 | 12 | * | ( ) | D6/D5 = 32*6!/16/5! = 12 | |
| A5 | {3,3,3,3} | 6 | 15 | 20 | 0 | 15 | 0 | 6 | * | 32 | D6/A5 = 32*6!/6! = 32 | |||
Images[]
| Coxeter plane | B6 | |
|---|---|---|
| Graph | 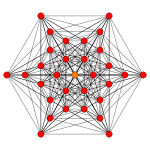
| |
| Dihedral symmetry | [12/2] | |
| Coxeter plane | D6 | D5 |
| Graph | 
|
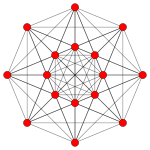
|
| Dihedral symmetry | [10] | [8] |
| Coxeter plane | D4 | D3 |
| Graph | 
|
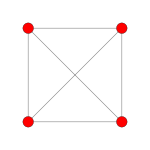
|
| Dihedral symmetry | [6] | [4] |
| Coxeter plane | A5 | A3 |
| Graph | 
|
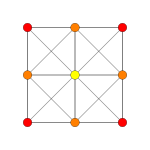
|
| Dihedral symmetry | [6] | [4] |
Related polytopes[]
There are 47 uniform polytopes with D6 symmetry, 31 are shared by the B6 symmetry, and 16 are unique:
| D6 polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 h{4,34} |
 h2{4,34} |
 h3{4,34} |
 h4{4,34} |
 h5{4,34} |
 h2,3{4,34} |
 h2,4{4,34} |
 h2,5{4,34} | ||||
 h3,4{4,34} |
 h3,5{4,34} |
 h4,5{4,34} |
 h2,3,4{4,34} |
 h2,3,5{4,34} |
 h2,4,5{4,34} |
 h3,4,5{4,34} |
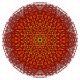 h2,3,4,5{4,34} | ||||
The 6-demicube, 131 is third in a dimensional series of uniform polytopes, expressed by Coxeter as k31 series. The fifth figure is a Euclidean honeycomb, 331, and the final is a noncompact hyperbolic honeycomb, 431. Each progressive uniform polytope is constructed from the previous as its vertex figure.
| n | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|
| Coxeter group |
A3A1 | A5 | D6 | E7 | = E7+ | =E7++ |
| Coxeter diagram |
||||||
| Symmetry | [3−1,3,1] | [30,3,1] | [31,3,1] | [32,3,1] | [33,3,1] | [34,3,1] |
| Order | 48 | 720 | 23,040 | 2,903,040 | ∞ | |
| Graph | 
|

|

|

|
- | - |
| Name | −131 | 031 | 131 | 231 | 331 | 431 |
It is also the second in a dimensional series of uniform polytopes and honeycombs, expressed by Coxeter as 13k series. The fourth figure is the Euclidean honeycomb 133 and the final is a noncompact hyperbolic honeycomb, 134.
| Space | Finite | Euclidean | Hyperbolic | |||
|---|---|---|---|---|---|---|
| n | 4 | 5 | 6 | 7 | 8 | 9 |
| Coxeter group |
A3A1 | A5 | D6 | E7 | =E7+ | =E7++ |
| Coxeter diagram |
||||||
| Symmetry | [3−1,3,1] | [30,3,1] | [31,3,1] | [32,3,1] | [[33,3,1]] | [34,3,1] |
| Order | 48 | 720 | 23,040 | 2,903,040 | ∞ | |
| Graph | 
|

|

|
- | - | |
| Name | 13,-1 | 130 | 131 | 132 | 133 | |
Skew icosahedron[]
Coxeter identified a subset of 12 vertices that form a regular skew icosahedron {3, 5} with the same symmetries as the icosahedron itself, but at different angles. He dubbed this the regular skew icosahedron.[4][5]
References[]
- ^ Coxeter, Regular Polytopes, sec 1.8 Configurations
- ^ Coxeter, Complex Regular Polytopes, p.117
- ^ Klitzing, Richard. "x3o3o *b3o3o3o - hax".
- ^ Coxeter, H. S. M. The beauty of geometry : twelve essays (Dover ed.). Dover Publications. pp. 450–451. ISBN 9780486409191.
- ^ Deza, Michael; Shtogrin, Mikhael (2000). "Embedding the graphs of regular tilings and star-honeycombs into the graphs of hypercubes and cubic lattices". Advanced Studies in Pure Mathematics: 77. doi:10.2969/aspm/02710073. Retrieved 4 April 2020.
- H.S.M. Coxeter:
- Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1n1)
- Klitzing, Richard. "6D uniform polytopes (polypeta) x3o3o *b3o3o3o – hax".
External links[]
- Olshevsky, George. "Demihexeract". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Multi-dimensional Glossary
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform polychoron | Pentachoron | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
- 6-polytopes


