Order-4 square hosohedral honeycomb

Order-4 square hosohedral honeycomb
Centrally projected onto a sphere
Type	Degenerate regular honeycomb
Schläfli symbol	{2,4,4}
Coxeter diagrams
Cells	{2,4}
Faces	{2}
Edge figure	{4}
Vertex figure	{4,4}
Dual
Coxeter group	[2,4,4]
Properties	Regular

In geometry, the order-4 square hosohedral honeycomb is a regular space-filling tessellation (or honeycomb) with Schläfli symbol {2,4,4}. It has 4 square hosohedra {2,4} around each edge. In other words, it is a packing of infinitely tall square columns. It is a degenerate honeycomb in Euclidean space, but can be seen as a projection onto the sphere. Its vertex figure, a square tiling is seen on each hemisphere.

Images[]

Stereographic projections of spherical projection, with all edges being projected into circles.

Centered on pole

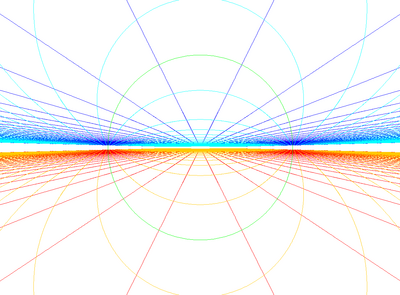Centered on equator

Related honeycombs[]

It is a part of a sequence of honeycombs with a square tiling vertex figure:

{p,4,4} honeycombs v
Space	E3	H3
Form	Affine	Paracompact		Noncompact
Name	{2,4,4}	{3,4,4}	{4,4,4}	{5,4,4}	{6,4,4}	..{∞,4,4}
Coxeter
Image
Cells	{2,4}	{3,4}	{4,4}	{5,4}	{6,4}	{∞,4}

Truncated order-4 square hosohedral honeycomb[]

Order-2 square tiling honeycomb Truncated order-4 square hosohedral honeycomb Partial tessellation with alternately colored cubes
Type	uniform convex honeycomb
Schläfli symbol	{4,4}×{}
Coxeter diagrams
Cells	{3,4}
Faces	{4}
Vertex figure	Square pyramid
Dual
Coxeter group	[2,4,4]
Properties	Uniform

The {2,4,4} honeycomb can be truncated as t{2,4,4} or {}×{4,4}, Coxeter diagram , seen as a layer of cubes, partially shown here with alternately colored cubic cells. Thorold Gosset identified this semiregular infinite honeycomb as a cubic semicheck.

The alternation of this honeycomb, , consists of infinite square pyramids and infinite tetrahedrons, between 2 square tilings.

See also[]

• Order-6 triangular hosohedral honeycomb
• Order-7 tetrahedral honeycomb
• List of regular polytopes

References[]

• The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN 0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space)