Order-4-4 pentagonal honeycomb

Order-4-4 pentagonal honeycomb
Type	Regular honeycomb
Schläfli symbol	{5,4,4} {5,41,1}
Coxeter diagram
Cells	{5,4}
Faces	{5}
Vertex figure	{4,4}
Dual	{4,4,5}
Coxeter group	[5,4,4] [5,41,1]
Properties	Regular

In the geometry of hyperbolic 3-space, the order-4-4 pentagonal honeycomb a regular space-filling tessellation (or honeycomb). Each infinite cell consists of a pentagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.

Geometry[]

The Schläfli symbol of the order-4-4 pentagonal honeycomb is {5,4,4}, with four order-4 pentagonal tilings meeting at each edge. The vertex figure of this honeycomb is a square tiling, {4,4}.

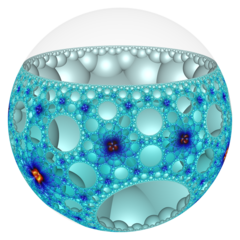Poincaré disk model

Ideal surface

Related polytopes and honeycombs[]

It is a part of a series of regular polytopes and honeycombs with {p,4,4} Schläfli symbol, and square tiling vertex figures:

{p,4,4} honeycombs v
Space	E3	H3
Form	Affine	Paracompact		Noncompact
Name	{2,4,4}	{3,4,4}	{4,4,4}	{5,4,4}	{6,4,4}	..{∞,4,4}
Coxeter
Image
Cells	{2,4}	{3,4}	{4,4}	{5,4}	{6,4}	{∞,4}

Order-4-4 hexagonal honeycomb[]

Order-4-4 hexagonal honeycomb
Type	Regular honeycomb
Schläfli symbol	{6,4,4} {6,41,1}
Coxeter diagram
Cells	{6,4}
Faces	{6}
Vertex figure	{4,4}
Dual	{4,4,6}
Coxeter group	[6,4,4] [6,41,1]
Properties	Regular

In the geometry of hyperbolic 3-space, the order-4-4 hexagonal honeycomb a regular space-filling tessellation (or honeycomb). Each infinite cell consists of an order-4 hexagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.

The Schläfli symbol of the octagonal tiling honeycomb is {6,4,4}, with three octagonal tilings meeting at each edge. The vertex figure of this honeycomb is a square tiling, {4,4}.

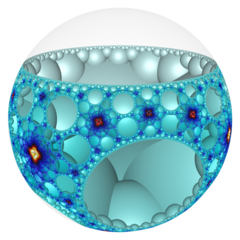Poincaré disk model

Ideal surface

Order-4-4 apeirogonal honeycomb[]

Order-4-4 apeirogonal honeycomb
Type	Regular honeycomb
Schläfli symbol	{∞,4,4} {∞,41,1}
Coxeter diagram
Cells	{∞,4}
Faces	{∞}
Vertex figure	{4,4}
Dual	{4,4,∞}
Coxeter group	[∞,4,4] [∞,41,1]
Properties	Regular

In the geometry of hyperbolic 3-space, the order-4-4 apeirogonal honeycomb a regular space-filling tessellation (or honeycomb). Each infinite cell consists of an order-4 apeirogonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.

The Schläfli symbol of the apeirogonal tiling honeycomb is {∞,4,4}, with three order-4 apeirogonal tilings meeting at each edge. The vertex figure of this honeycomb is a square tiling, {4,4}.

Poincaré disk model

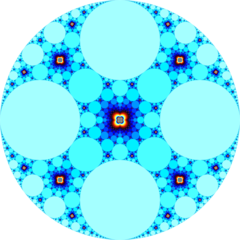Ideal surface

See also[]

• Convex uniform honeycombs in hyperbolic space
• List of regular polytopes

References[]

• Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
• The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN 0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space) Table III
• Jeffrey R. Weeks The Shape of Space, 2nd edition ISBN 0-8247-0709-5 (Chapters 16–17: Geometries on Three-manifolds I,II)
• George Maxwell, Sphere Packings and Hyperbolic Reflection Groups, JOURNAL OF ALGEBRA 79,78-97 (1982) [1]
• Hao Chen, Jean-Philippe Labbé, Lorentzian Coxeter groups and Boyd-Maxwell ball packings, (2013)[2]
• Visualizing Hyperbolic Honeycombs arXiv:1511.02851 Roice Nelson, Henry Segerman (2015)

External links[]

• John Baez, Visual insights: {7,3,3} Honeycomb (2014/08/01) {7,3,3} Honeycomb Meets Plane at Infinity (2014/08/14)
• Danny Calegari, Kleinian, a tool for visualizing Kleinian groups, Geometry and the Imagination 4 March 2014. [3]