Leap year

This article needs additional citations for verification. Please help by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources:  –  ·  ·  · scholar · JSTOR (February 2020) (Learn how and when to remove this template message)

A leap year (also known as an intercalary year or bissextile year) is a calendar year that contains an additional day (or, in the case of a lunisolar calendar, a month) added to keep the calendar year synchronized with the astronomical year or seasonal year.^[1] Because astronomical events and seasons do not repeat in a whole number of days, calendars that have a constant number of days in each year will unavoidably drift over time with respect to the event that the year is supposed to track, such as seasons. By inserting (called intercalating in technical terminology) an additional day or month into some years, the drift between a civilization's dating system and the physical properties of the solar system can be corrected. A year that is not a leap year is a common year.

For example, in the Gregorian calendar, each leap year has 366 days instead of 365, by extending February to 29 days rather than the common 28. These extra days occur in each year which is an integer multiple of 4 (except for years evenly divisible by 100, but not by 400). The leap year of 366 days has 52 weeks and two days, hence the year following a leap year will start later by two days of the week.

In the lunisolar Hebrew calendar, Adar Aleph, a 13th lunar month, is added seven times every 19 years to the twelve lunar months in its common years to keep its calendar year from drifting through the seasons. In the Bahá'í Calendar, a leap day is added when needed to ensure that the following year begins on the March equinox.

The term leap year probably comes from the fact that a fixed date in the Gregorian calendar normally advances one day of the week from one year to the next, but the day of the week in the 12 months following the leap day (from March 1 through February 28 of the following year) will advance two days due to the extra day, thus leaping over one day in the week.^[2][3] For example, Christmas Day (December 25) fell on a Friday in 2020, falls on a Saturday in 2021, a Sunday in 2022 and a Monday in 2023, but then will leap over Tuesday to fall on a Wednesday in 2024.

The length of a day is also occasionally corrected by inserting a leap second into Coordinated Universal Time (UTC) because of variations in Earth's rotation period. Unlike leap days, leap seconds are not introduced on a regular schedule because variations in the length of the day are not entirely predictable.

Leap years can present a problem in computing, known as the leap year bug, when a year is not correctly identified as a leap year or when February 29 is not handled correctly in logic that accepts or manipulates dates.

Julian calendar[]

On 1 January AUC 709 (45 BC), by edict, Julius Caesar reformed the historic Roman calendar to make it a consistent solar calendar (rather than one which was neither strictly lunar nor strictly solar), thus removing the need for frequent intercalary months. His rule for leap years was a simple one: add a leap day every four years. This algorithm is close to reality: a Julian year lasts 365.25 days, a mean tropical year about 365.2422 days. Consequently, the calendar drifts out 'true' by about three days every 400 years. The Julian calendar continued in use unaltered for about 1600 years until the Catholic Church became concerned about the widening divergence between the March Equinox and 21 March, as explained below.

In the modern calendar, leap day falls on 29 February. This was not always the case: when the Julian calendar was introduced, leap day was handled differently in two respects. First, leap day fell within February and not at the end. Second, the leap day was simply not counted so that a leap year still had 365 days.^[4]

The Romans treated leap day as a second sixth day before the Kalends (first day) of March, in Latin ante diem bis sextum Kalendas Martias. This bis sextum was translated as 'bissextile': the 'bissextile day' is the leap day and a 'bissextile year' is a year which includes a leap day.^[4] This second instance of the sixth day before the Kalends of March was inserted in calendars between the 'normal' fifth and sixth days. By a legal fiction, the Romans treated both the first "sixth day" and the additional "sixth day" before the Kalends of March as one day. Thus a child born on either of those days in a leap year would have its first birthday on the following sixth day before the Kalends of March. When, many years later, modern consecutive day counts were laid alongside the Roman dates the sixth day before the Kalends of March fell on 24 February. However, in a leap year the sixth day fell on 25 February because the additional sixth day came before the 'normal' sixth day.^[5]

The medieval Church continued the Roman practice which can be illustrated by, for example, the feast of Saint Matthias which used to be celebrated on the sixth day before the Kalends of March in both common and leap years. The calendar for February in the Book of Common Prayer of 1549 shows the position in a normal year when the feast of St Matthias is on the sixth day of the Kalends of March which is alongside 24 February. The position in a leap year is not shown in the Church of England's 1549 Book of Common Prayer but the prior insertion of the second sixth day meant the feast of St Matthias fell on 25 February in leap years. This practice ended in England some time after Henry VIII split from Rome, specifically in the 1662 edition of the Book of Common Prayer.^[6] Consecutive day counting has entirely replaced the Roman system. The feast of St Matthias is invariably on 24 February and leap day is shown at the end of February.^{[7] [a]}

The Church and civil society also continued the Roman practice whereby the leap day was simply not counted so that a leap year was only reckoned as 365 days. Henry III of England's Statute De Anno et Die Bissextili^[b] of 1236^[9] instructed magistrates to ignore the leap day when persons were being ordered to appear before the court within a year.^[8] The practical application of the rule is obscure. It was regarded as in force in the time of the famous lawyer Sir Edward Coke (1552-1634) because he cites it in his Institutes of the Lawes of England. However, Coke merely quotes the act with a short translation and does not give practical examples.^[10]

` ... and by (b) the statute de anno bissextili, it is provided, quod computentur dies ille excrescens et dies proxime præcedens pro unico dii, so as in computation that day excrescent is not accounted.'

Gregorian calendar[]

An image showing which century years are leap years in the Gregorian calendar

In the Gregorian calendar, the standard calendar in most of the world, most years that are multiples of 4 are leap years. In each leap year, the month of February has 29 days instead of 28. Adding one extra day in the calendar every four years compensates for the fact that a period of 365 days is shorter than a tropical year by almost 6 hours.^[11] Some exceptions to this basic rule are required since the duration of a tropical year is slightly less than 365.25 days. The Gregorian reform modified the Julian calendar's scheme of leap years as follows:

Every year that is exactly divisible by four is a leap year, except for years that are exactly divisible by 100, but these centurial years are leap years if they are exactly divisible by 400. For example, the years 1700, 1800, and 1900 are not leap years, but the years 1600 and 2000 are.^[12]

Over a period of four centuries, the accumulated error of adding a leap day every four years amounts to about three extra days. The Gregorian calendar therefore omits three leap days every 400 years, which is the length of its leap cycle. This is done by omitting February 29 in the three century years (multiples of 100) that are not multiples of 400.^[13][14] The years 2000 and 2400 are leap years, but not 1700, 1800, 1900, 2100, 2200 and 2300. By this rule, an entire leap cycle is 400 years which total 146,097 days, and the average number of days per year is 365 + 1⁄4 − 1⁄100 + 1⁄400 = 365 + 97⁄400  = 365.2425.^[15] The rule can be applied to years before the Gregorian reform (the proleptic Gregorian calendar), and before the year 1 if astronomical year numbering is used.^[16]

This graph shows the variations in date and time of the June Solstice due to unequally spaced "leap day" rules. Contrast this with the Iranian Solar Hijri calendar, which generally has 8 leap year days every 33 years.

The Gregorian calendar was designed to keep the vernal equinox on or close to March 21, so that the date of Easter (celebrated on the Sunday after the ecclesiastical full moon that falls on or after March 21) remains close to the vernal equinox.^[17] The "Accuracy" section of the "Gregorian calendar" article discusses how well the Gregorian calendar achieves this design goal, and how well it approximates the tropical year.

Algorithm[]

The following pseudocode determines whether a year is a leap year or a common year in the Gregorian calendar (and in the proleptic Gregorian calendar before 1582). The year variable being tested is the integer representing the number of the year in the Gregorian calendar.

The algorithm applies to proleptic Gregorian calendar years before 1, but only if the year is expressed with astronomical year numbering instead of the BC or BCE notation. The algorithm is not necessarily valid for years in the Julian calendar, such as years before 1752 in the British Empire: for example, the year 1700 was a leap year in the Julian calendar, but not in the Gregorian calendar.

Leap day[]

A Swedish pocket calendar from 2008 showing February 29

February 1900 calendar showing that 1900 was not a leap year

February 29 is a date that usually occurs every four years, and is called the leap day. This day is added to the calendar in leap years as a corrective measure because the Earth does not orbit the sun in precisely 365 days.

The Gregorian calendar is a modification of the Julian calendar first used by the Romans. The Roman calendar originated as a lunisolar calendar and named many of its days after the syzygies of the moon: the new moon (Kalendae or calends, hence "calendar") and the full moon (Idus or ides). The Nonae or nones was not the first quarter moon but was exactly one nundina or Roman market week of nine days before the ides, inclusively counting the ides as the first of those nine days. This is what we would call a period of eight days. In 1825, Ideler believed that the lunisolar calendar was abandoned about 450 BC by the decemvirs, who implemented the Roman Republican calendar, used until 46 BC. The days of these calendars were counted down (inclusively) to the next named day, so February 24 was ante diem sextum Kalendas Martias ("the sixth day before the calends of March") often abbreviated a. d. VI Kal. Mart. The Romans counted days inclusively in their calendars, so this was actually the fifth day before March 1 when counted in the modern exclusive manner (not including the starting day).^[18]

The Republican calendar's intercalary month was inserted on the first or second day after the Terminalia (a. d. VII Kal. Mar., February 23). The remaining days of Februarius were dropped. This intercalary month, named Intercalaris or Mercedonius, contained 27 days. The religious festivals that were normally celebrated in the last five days of February were moved to the last five days of Intercalaris. Because only 22 or 23 days were effectively added, not a full lunation, the calends and ides of the Roman Republican calendar were no longer associated with the new moon and full moon.

The Julian calendar, which was developed in 46 BC by Julius Caesar, and became effective in 45 BC, distributed an extra ten days among the months of the Roman Republican calendar. Caesar also replaced the intercalary month by a single intercalary day, located where the intercalary month used to be. To create the intercalary day, the existing ante diem sextum Kalendas Martias (February 24) was doubled, producing ante diem bis sextum Kalendas Martias. Hence, the year containing the doubled day was a bissextile (bis sextum, "twice sixth") year. For legal purposes, the two days of the bis sextum were considered to be a single day, with the second half being intercalated; but in common practice by 238, when Censorinus wrote, the intercalary day was followed by the last five days of February, a. d. VI, V, IV, III and pridie Kal. Mart. (the days numbered 24, 25, 26, 27, and 28 from the beginning of February in a common year), so that the intercalated day was the first half of the doubled day. Thus the intercalated day was effectively inserted between the 23rd and 24th days of February. All later writers, including Macrobius about 430, Bede in 725, and other medieval computists (calculators of Easter), continued to state that the bissextum (bissextile day) occurred before the last five days of February.

In the older Roman Missal, feast days falling on or after February 24 are celebrated one day later in a leap year.

Until 1970, the Roman Catholic Church always celebrated the feast of Saint Matthias on a. d. VI Kal. Mart., so if the days were numbered from the beginning of the month, it was named February 24 in common years, but the presence of the bissextum in a bissextile year immediately before a. d. VI Kal. Mart. shifted the latter day to February 25 in leap years, with the Vigil of St. Matthias shifting from February 23 to the leap day of February 24. This shift did not take place in pre-Reformation Norway and Iceland; Pope Alexander III ruled that either practice was lawful (Liber Extra, 5. 40. 14. 1). Other feasts normally falling on February 25–28 in common years are also shifted to the following day in a leap year (although they would be on the same day according to the Roman notation). The practice is still observed by those who use the older calendars.

Synchronized calendars (Bengali, Indian and Thai)[]

The Revised Bengali Calendar of Bangladesh and the Indian National Calendar organise their leap years so that every leap day is close to February 29 in the Gregorian calendar and vice versa. This makes it easy to convert dates to or from Gregorian.

The Thai solar calendar uses the Buddhist Era (BE) but has been synchronized with the Gregorian since AD 1941.

Julian, Coptic and Ethiopian calendars[]

The Julian calendar was instituted in 45 BC at the order of Julius Caesar, and the original intent was to make every fourth year a leap year, but this was not carried out correctly. Augustus ordered some leap years to be omitted to correct the problem, and by AD 8 the leap years were being observed every fourth year, and the observances were consistent up to and including modern times.

From AD 8 the Julian calendar received an extra day added to February in years that are multiples of 4 (although the AD year numbering system was not introduced until AD 525).

The Coptic calendar and Ethiopian calendar also add an extra day to the end of the year once every four years before a Julian 29-day February.

This rule gives an average year length of 365.25 days. However, it is 11 minutes longer than a tropical year. This means that the vernal equinox moves a day earlier in the calendar about every 131 years.

Revised Julian calendar[]

The Revised Julian calendar adds an extra day to February in years that are multiples of four, except for years that are multiples of 100 that do not leave a remainder of 200 or 600 when divided by 900. This rule agrees with the rule for the Gregorian calendar until 2799. The first year that dates in the Revised Julian calendar will not agree with those in the Gregorian calendar will be 2800, because it will be a leap year in the Gregorian calendar but not in the Revised Julian calendar.

This rule gives an average year length of 365.242222 days. This is a very good approximation to the mean tropical year, but because the vernal equinox year is slightly longer, the Revised Julian calendar, for the time being, does not do as good a job as the Gregorian calendar at keeping the vernal equinox on or close to March 21.

Chinese calendar[]

The Chinese calendar is lunisolar, so a leap year has an extra month, often called an embolismic month after the Greek word for it. In the Chinese calendar, the leap month is added according to a rule which ensures that month 11 is always the month that contains the northern winter solstice. The intercalary month takes the same number as the preceding month; for example, if it follows the second month (二月) then it is simply called "leap second month" i.e. simplified Chinese: 闰二月; traditional Chinese: 閏二月; pinyin: rùn'èryuè.

Hebrew calendar[]

The Hebrew calendar is lunisolar with an embolismic month. This extra month is called Adar Alef (first Adar) and is added before Adar, which then becomes Adar Bet (second Adar). According to the Metonic cycle, this is done seven times every nineteen years (specifically, in years 3, 6, 8, 11, 14, 17, and 19). This is to ensure that Passover (Pesah) is always in the spring as required by the Torah (Pentateuch) in many verses^[19] relating to Passover.

In addition, the Hebrew calendar has postponement rules that postpone the start of the year by one or two days. These postponement rules reduce the number of different combinations of year length and starting days of the week from 28 to 14, and regulate the location of certain religious holidays in relation to the Sabbath. In particular, the first day of the Hebrew year can never be Sunday, Wednesday or Friday. This rule is known in Hebrew as "lo adu rosh" (לא אד״ו ראש), i.e., "Rosh [ha-Shanah, first day of the year] is not Sunday, Wednesday or Friday" (as the Hebrew word adu is written by three Hebrew letters signifying Sunday, Wednesday and Friday). Accordingly, the first day of Passover is never Monday, Wednesday or Friday. This rule is known in Hebrew as "lo badu Pesah" (לא בד״ו פסח), which has a double meaning — "Passover is not a legend", but also "Passover is not Monday, Wednesday or Friday" (as the Hebrew word badu is written by three Hebrew letters signifying Monday, Wednesday and Friday).

One reason for this rule is that Yom Kippur, the holiest day in the Hebrew calendar and the tenth day of the Hebrew year, now must never be adjacent to the weekly Sabbath (which is Saturday), i.e., it must never fall on Friday or Sunday, in order not to have two adjacent Sabbath days. However, Yom Kippur can still be on Saturday. A second reason is that Hoshana Rabbah, the 21st day of the Hebrew year, will never be on Saturday. These rules for the Feasts do not apply to the years from the Creation to the deliverance of the Hebrews from Egypt under Moses. It was at that time (cf. Exodus 13) that the God of Abraham, Isaac and Jacob gave the Hebrews their "Law" including the days to be kept holy and the feast days and Sabbaths.

Years consisting of 12 months have between 353 and 355 days. In a k'sidra ("in order") 354-day year, months have alternating 30 and 29 day lengths. In a chaser ("lacking") year, the month of Kislev is reduced to 29 days. In a malei ("filled") year, the month of Marcheshvan is increased to 30 days. 13-month years follow the same pattern, with the addition of the 30-day Adar Alef, giving them between 383 and 385 days.

Islamic calendar[]

The observed and calculated versions of the Islamic calendar do not have regular leap days, even though both have lunar months containing 29 or 30 days, generally in alternating order. However, the tabular Islamic calendar used by Islamic astronomers during the Middle Ages and still used by some Muslims does have a regular leap day added to the last month of the lunar year in 11 years of a 30-year cycle.^[20] This additional day is found at the end of the last month, Dhu al-Hijjah, which is also the month of the Hajj.^[21]

The Hijri-Shamsi calendar, also adopted by the Ahmadiyya Community, is based on solar calculations and is similar to the Gregorian calendar in its structure with the exception that the first year starts with Hijra.^[22]

Baháʼí calendar[]

The Baháʼí calendar is a solar calendar composed of 19 months of 19 days each (361 days). Years begin at Naw-Rúz, on the vernal equinox, on or about March 21. A period of "Intercalary Days", called Ayyam-i-Ha, is inserted before the 19th month. This period normally has 4 days, but an extra day is added when needed to ensure that the following year starts on the vernal equinox. This is calculated and known years in advance.

Solar Hijri calendar[]

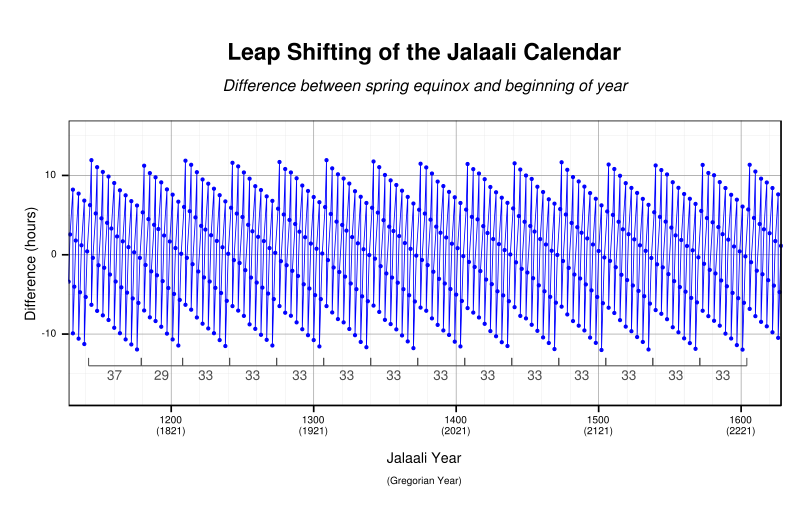
The Iranian calendar is an observational calendar that starts on the spring equinox and adds a single intercalated day to the last month (Esfand) once every four or five years; the first leap year occurs as the fifth year of the typical 33-year cycle and the remaining leap years occur every four years through the remainder of the 33-year cycle. This system has less periodic deviation or jitter from its mean year than the Gregorian calendar and operates on the simple rule that the vernal equinox always falls in the 24-hour period ending at noon on New Year's Day.^[23] The 33-year period is not completely regular; every so often the 33-year cycle will be broken by a cycle of 29 years.^[24] A similar rule has been proposed to simplify the Gregorian calendar.^[25] The centennial leap years would be spaced so that in years giving remainder 3 on division by 100 the dynamic mean sun^[26] passes through the equinox in the 24-hour period ending at 1 PM GMT on 19 March. The system would be introduced when for the first time the dynamic mean sun is due to pass through the equinox before 1 PM GMT on 18 March in a year giving remainder 3 on division by 400. The immediately preceding centennial leap year will be cancelled. The first cancellation will probably be AD 8400 and the next two centennial leap years thereafter will probably be AD 8800 and AD 9700.^[27]

Folk traditions[]

A spinster eagerly awaits the upcoming leap day, in this 1903 cartoon by Bob Satterfield.

In Ireland and Britain, it is a tradition that women may propose marriage only in leap years. While it has been claimed that the tradition was initiated by Saint Patrick or Brigid of Kildare in 5th century Ireland, this is dubious, as the tradition has not been attested before the 19th century.^[28] Supposedly, a 1288 law by Queen Margaret of Scotland (then age five and living in Norway), required that fines be levied if a marriage proposal was refused by the man; compensation was deemed to be a pair of leather gloves, a single rose, £1 and a kiss.^[29] In some places the tradition was tightened to restricting female proposals to the modern leap day, February 29, or to the medieval (bissextile) leap day, February 24.

According to Felten: "A play from the turn of the 17th century, 'The Maydes Metamorphosis,' has it that 'this is leape year/women wear breeches.' A few hundred years later, breeches wouldn't do at all: Women looking to take advantage of their opportunity to pitch woo were expected to wear a scarlet petticoat — fair warning, if you will."^[30]

In Finland, the tradition is that if a man refuses a woman's proposal on leap day, he should buy her the fabrics for a skirt.^[31]

In France, since 1980, a satirical newspaper entitled La Bougie du Sapeur is published only on leap year, on February 29.

In Greece, marriage in a leap year is considered unlucky.^[32] One in five engaged couples in Greece will plan to avoid getting married in a leap year.^[33]

In February 1988 the town of Anthony in Texas, declared itself "leap year capital of the world", and an international leapling birthday club was started.^[34]

• 1908 postcards
• 

  Woman capturing man with butterfly-net

• 

  Women anxiously awaiting January 1

• 

  Histrionically preparing

Birthdays[]

A person born on February 29 may be called a "leapling" or a "leaper".^[35] In common years, they usually celebrate their birthdays on February 28. In some situations, March 1 is used as the birthday in a non-leap year, since it is the day following February 28.

Technically, a leapling will have fewer birthday anniversaries than their age in years. This phenomenon is exploited when a person claims to be only a quarter of their actual age, by counting their leap-year birthday anniversaries only: for example, in Gilbert and Sullivan's 1879 comic opera The Pirates of Penzance, Frederic the pirate apprentice discovers that he is bound to serve the pirates until his 21st birthday (that is, when he turns 88 years old, since 1900 was not a leap year) rather than until his 21st year.

For legal purposes, legal birthdays depend on how local laws count time intervals.

Taiwan[]

Wikisource has original text related to this article: Civil Code Part I General Principles

The Civil Code of the Taiwan since October 10, 1929,^[36] implies that the legal birthday of a leapling is February 28 in common years:

If a period fixed by weeks, months, and years does not commence from the beginning of a week, month, or year, it ends with the ending of the day which precedes the day of the last week, month, or year which corresponds to that on which it began to commence. But if there is no corresponding day in the last month, the period ends with the ending of the last day of the last month.^[37]

Hong Kong[]

Since 1990 non-retroactively, Hong Kong considers the legal birthday of a leapling March 1 in common years:^[38]

1. The time at which a person attains a particular age expressed in years shall be the commencement of the anniversary corresponding to the date of [their] birth.
2. Where a person has been born on February 29 in a leap year, the relevant anniversary in any year other than a leap year shall be taken to be March 1.
3. This section shall apply only where the relevant anniversary falls on a date after the date of commencement of this Ordinance.

See also[]

• Century leap year
• Calendar reform includes proposals that have not (yet) been adopted.
• Leap second
• Leap week calendar
• Leap year bug
• Sansculottides
• Zeller's congruence

Notes[]

References[]

External links[]

• Gray, Meghan. "29 Leap Year". Numberphile. Brady Haran. Archived from the original on 2017-05-22. Retrieved 2013-04-06.
• Famous Leapers
• Leap Day Campaign: Galileo Day
• History Behind Leap Year National Geographic Society