Coombs' method

Part of the Politics series
Electoral systems
show Plurality/majoritarian Plurality First-past-the-post Single non-transferable vote Limited voting Plurality-at-large (block voting) General ticket Multi-round voting Two-round Exhaustive ballot Ranked / preferential systems Instant-runoff (alternative vote) Contingent vote Coombs' method Condorcet methods (Copeland's, Dodgson's, Kemeny–Young, Minimax, Nanson's, ranked pairs, Schulze, Alternative Smith) Positional voting (Borda count, Nauru/Dowdall method) Bucklin voting Oklahoma primary electoral system Preferential block voting Cardinal / graded systems Score voting Approval voting (unified primary) Combined approval voting Usual judgment Satisfaction approval voting Majority judgment STAR voting
show Proportional representation Party-list (open lists, closed lists, local lists) Highest averages (D'Hondt, Sainte-Laguë, Huntington–Hill) Largest remainder (Hare, Droop, Imperiali, Hagenbach-Bischoff) Proportional forms of ranked voting Single transferable vote (Gregory, Wright) CPO-STV Schulze STV Proportional forms of approval voting Proportional approval voting Sequential proportional approval voting Biproportional apportionment Fair majority voting Weighted voting Direct representation Interactive representation Liquid democracy
show Mixed systems Non-compensatory mixed systems Parallel voting (mixed-member majoritarian) Compensatory mixed systems Mixed-member proportional Additional member system Mixed single vote (positive vote transfer) Scorporo (negative vote transfer) Alternative Vote Plus Dual-member proportional Rural–urban proportional Other mixed systems Majority bonus
show Other systems and related theory Cumulative voting Binomial voting Proxy voting Delegated voting Random selection (sortition, random ballot) Comparison of electoral systems Social choice theory Arrow's theorem Gibbard–Satterthwaite theorem Public choice theory
Politics portal
v t

Coombs' method (or the Coombs rule)^[1] is a ranked voting system created by Clyde Coombs used for single-winner elections. Similarly to instant-runoff voting, it uses candidate elimination and redistribution of votes cast for that candidate until one candidate has a majority of votes.

Procedures[]

Each voter rank-orders all of the candidates on their ballot. If at any time one candidate is ranked first (among non-eliminated candidates) by an absolute majority of the voters, that candidate wins. Otherwise, the candidate ranked last (again among non-eliminated candidates) by the largest number of (or a plurality of) voters is eliminated. Conversely, under instant-runoff voting, the candidate ranked first (among non-eliminated candidates) by the fewest voters is eliminated.

In some sources, the elimination proceeds regardless of whether any candidate is ranked first by a majority of voters, and the last candidate to be eliminated is the winner.^[2] This variant of the method can result in a different winner than the former one (unlike in instant-runoff voting, where checking to see if any candidate is ranked first by a majority of voters is only a shortcut that does not affect the outcome).

An example[]

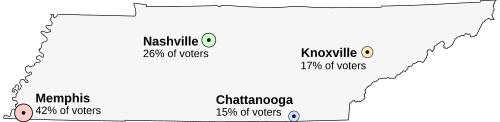
Imagine that Tennessee is having an election on the location of its capital. The population of Tennessee is concentrated around its four major cities, which are spread throughout the state. For this example, suppose that the entire electorate lives in these four cities and that everyone wants to live as near to the capital as possible.

The candidates for the capital are:

• Memphis, the state's largest city, with 42% of the voters, but located far from the other cities
• Nashville, with 26% of the voters, near the center of the state
• Knoxville, with 17% of the voters
• Chattanooga, with 15% of the voters

The preferences of the voters would be divided like this:

Assuming all of the voters vote sincerely (strategic voting is discussed below), the results would be as follows, by percentage:

• In the first round, no candidate has an absolute majority of first-place votes (51).
• Memphis, having the most last-place votes (26+15+17=58), is therefore eliminated.
• In the second round, Memphis is out of the running, and so must be factored out. Memphis was ranked first on Group A's ballots, so the second choice of Group A, Nashville, gets an additional 42 first-place votes, giving it an absolute majority of first-place votes (68 versus 15+17=32), and making it the winner.
• Note that the last-place votes are only used to eliminate a candidate in a voting round where no candidate achieves an absolute majority; they are disregarded in a round where any candidate has 51% or more. Thus last-place votes play no role in the final round.

Use[]

The voting rounds used in the reality television program Survivor could be considered a variation of Coombs' method, with sequential voting rounds. Everyone votes for one candidate they support for elimination each round, and the candidate with a plurality of that vote is eliminated. A strategy difference is that sequential rounds of voting means the elimination choice is fixed in a ranked ballot Coombs' method until that candidate is eliminated.

Potential for strategic voting[]

The Coombs' method is vulnerable to three tactical voting strategies:^{[citation needed]} compromising, push-over, and teaming. Coombs is sensitive to incomplete ballots, and how voters fill in the bottom of their ballots makes a big difference.^[3]

See also[]

• List of democracy and elections-related topics

Notes[]