E₈ polytope

Orthographic projections in the E₈ Coxeter plane
4₂₁	2₄₁	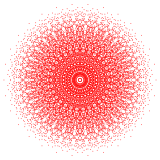1₄₂

In 8-dimensional geometry, there are 255 uniform polytopes with E₈ symmetry. The three simplest forms are the 4₂₁, 2₄₁, and 1₄₂ polytopes, composed of 240, 2160 and 17280 vertices respectively.

These polytopes can be visualized as symmetric orthographic projections in Coxeter planes of the E₈ Coxeter group, and other subgroups.

Graphs[]

Symmetric orthographic projections of these 255 polytopes can be made in the E₈, E₇, E₆, D₇, D₆, D₅, D₄, D₃, A₇, A₅ Coxeter planes. A_k has [k+1] symmetry, D_k has [2(k-1)] symmetry, and E₆, E₇, E₈ have [12], [18], [30] symmetry respectively. In addition there are two other degrees of fundamental invariants, order [20] and [24] for the E₈ group that represent Coxeter planes.

11 of these 255 polytopes are each shown in 14 symmetry planes, with vertices and edges drawn, and vertices colored by the number of overlapping vertices in each projective position.

#	Coxeter plane projections															Coxeter-Dynkin diagram Name
#	E₈ [30]	E₇ [18]	E₆ [12]	[24]	[20]	D₄-E₆ [6]	A₃ D₃ [4]	A₂ D₄ [6]	D₅ [8]	A₄ D₆ [10]	D₇ [12]	A₆ B₇ [14]	B₈ [16/2]	A₅ [6]	A₇ [8]	Coxeter-Dynkin diagram Name
1																4₂₁ (fy)
2																Rectified 4₂₁ (riffy)
3																Birectified 4₂₁ (borfy)
4																Trirectified 4₂₁ (torfy)
5																Rectified 1₄₂ (buffy)
6																Rectified 2₄₁ (robay)
7																2₄₁ (bay)
8
9																(tiffy)
10																1₄₂ (bif)
11

References[]

H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6^[1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
Klitzing, Richard. "8D uniform polytopes (polyzetta)".

Notes[]

^ Wiley::Kaleidoscopes: Selected Writings of H.S.M. Coxeter

v t Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	A_n	B_n	I₂(p) / D_n	E₆ / E₇ / E₈ / F₄ / G₂	H_n
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	Pentachoron	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	1₂₂ • 2₂₁
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	1₃₂ • 2₃₁ • 3₂₁
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	1₄₂ • 2₄₁ • 4₂₁
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1_k2 • 2_k1 • k₂₁	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds

[1] Wiley::Kaleidoscopes: Selected Writings of H.S.M. Coxeter

[1]

E8 polytope

Graphs[]

References[]

Notes[]

E₈ polytope