Symmetrohedron


In geometry, a symmetrohedron is a high-symmetry polyhedron containing convex regular polygons on symmetry axes with gaps on the convex hull filled by irregular polygons. The name was coined by Craig S. Kaplan and George W. Hart.[1]
The trivial cases are the Platonic solids, Archimedean solids with all regular polygons. A first class is called bowtie which contain pairs of trapezoidal faces. A second class has kite faces. Another class are called LCM symmetrohedra.
Symbolic notation[]
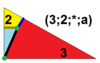
Each symmetrohedron is described by a symbolic expression G(l; m; n; α). G represents the symmetry group (T,O,I). The values l, m and n are the multipliers ; a multiplier of m will cause a regular km-gon to be placed at every k-fold axis of G. In the notation, the axis degrees are assumed to be sorted in descending order, 5,3,2 for I, 4,3,2 for O, and 3,3,2 for T . We also allow two special values for the multipliers: *, indicating that no polygons should be placed on the given axes, and 0, indicating that the final solid must have a vertex (a zero-sided polygon) on the axes. We require that one or two of l, m, and n be positive integers. The final parameter, α, controls the relative sizes of the non-degenerate axis-gons.
Conway polyhedron notation is another way to describe these polyhedra, starting with a regular form, and applying prefix operators. The notation doesn't imply which faces should be made regular beyond the uniform solutions of the Archimedean solids.
| I(*;2;3;e) | Pyritohedral |
|---|---|

|

|
1-generator point[]
These symmetrohedra are produced by a single generator point within a fundamental domains, reflective symmetry across domain boundaries. Edges exist perpendicular to each triangle boundary, and regular faces exist centered on each of the 3 triangle corners.
The symmetrohedra can be extended to euclidean tilings, using the symmetry of the regular square tiling, and dual pairs of triangular and hexagonal tilings. Tilings, Q is square symmetry p4m, H is hexagonal symmetry p6m.
Coxeter-Dynkin diagrams exist for these uniform polyhedron solutions, representing the position of the generator point within the fundamental domain. Each node represents one of 3 mirrors on the edge of the triangle. A mirror node is ringed if the generator point is active, off the mirror, and creates new edges between the point and its mirror image.
| Domain | Edges | Tetrahedral (3 3 2) | Octahedral (4 3 2) | Icosahedral (5 3 2) | Triangular (6 3 2) | Square (4 4 2) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symbol | Image | Symbol | Image | Symbol | Image | Symbol | Image | Dual | Symbol | Image | Dual | ||
 |
1 | T(1;*;*;e) T, |

|
C, O(1;*;*;e) |

|
I(1;*;*;e) D, |

|
H(1;*;*;e) H, |

|

|
Q(1;*;*;e) Q, |

|

|
 |
1 | T(*;1;*;e) dT, |

|
O(*;1;*;e) O, |

|
I(*;1;*;e) I, |

|
H(*;1;*;e) dH, |

|

|
Q(*;1;*;e) dQ, |

|

|
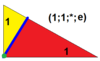 |
2 | T(1;1;*;e) aT, |

|
O(1;1;*;e) aC, |

|
I(1;1;*;e) aD, |

|
H(1;1;*;e) aH, |

|

|
Q(1;1;*;e) aQ, |

|

|
 |
3 | T(2;1;*;e) tT, |

|
O(2;1;*;e) tC, |

|
I(2;1;*;e) tD, |

|
H(2;1;*;e) tH, |

|

|
Q(2;1;*;e) tQ, |

|

|
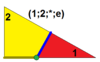 |
3 | T(1;2;*;e) dtT, |

|
O(1;2;*;e) tO, |

|
I(1;2;*;e) tI, |

|
H(1;2;*;e) dtH, |

|

|
Q(1;2;*;e) dtQ, |

|

|
 |
4 | T(1;1;*;1) eT, |

|
O(1;1;*;1) eC, |

|
I(1;1;*;1) eD, |

|
H(1;1;*;1) eH, |

|

|
Q(1;1;*;1) eQ, |

|

|
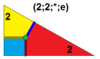 |
6 | T(2;2;*;e) bT, |

|
O(2;2;*;e) bC, |

|
I(2;2;*;e) bD, |

|
H(2;2;*;e) bH, |

|

|
Q(2;2;*;e) bQ, |

|

|
2-generator points[]
| Domain | Edges | Tetrahedral (3 3 2) | Octahedral (4 3 2) | Icosahedral (5 3 2) | Triangular (6 3 2) | Square (4 4 2) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symbol | Image | Symbol | Image | Symbol | Image | Symbol | Image | Dual | Symbol | Image | Dual | ||
 |
6 | T(1;2;*;[2]) atT |

|
O(1;2;*;[2]) atO |

|
I(1;2;*;[2]) atI |

|
H(1;2;*;[2]) atΔ |

|

|
Q(1;2;*;[2]) Q(2;1;*;[2]) atQ |
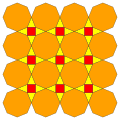
|

|
 |
6 | O(2;1;*;[2]) atC |

|
I(2;1;*;[2]) atD |

|
H(2;1;*;[2]) atH |

|

| |||||
 |
7 | T(3;*;*;[2]) T(*;3;*;[2]) dKdT |

|
O(3;*;*;[2]) dKdC |

|
I(3;*;*;[2]) dKdD |

|
H(3;*;*;[2]) dKdH |

|

|
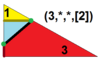
Q(3;*;*;[2]) Q(*;3;*;[2]) dKQ |
|

|
 |
7 | O(*;3;*;[2]) dKdO |

|
I(*;3;*;[2]) dKdI |

|
H(*;3;*;[2]) dKdΔ |

|

| |||||
 |
8 | T(2;3;*;α) T(3;2;*;α) dM0T |

|
O(2;3;*;α) dM0dO |

|
I(2;3;*;α) dM0dI |

|
H(2;3;*;α) dM0dΔ |

|

|
Q(2;3;*;α) Q(3;2;*;α) dM0Q |
|

|
 |
8 | O(3;2;*;α) dM0dC |

|
I(3;2;*;α) dM0dD |

|
H(3;2;*;α) dM0dH |

|

| |||||
 |
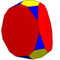
9 | T(2;4;*;e) T(4;2;*;e) ttT |
|
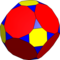
O(2;4;*;e) ttO |
|
I(2;4;*;e) ttI |

|
H(2;4;*;e) ttΔ |

|

|
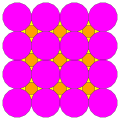
Q(4;2;*;e) Q(2;4;*;e) ttQ |
|

|
 |
9 | O(4;2;*;e) ttC |

|
I(4;2;*;e) ttD |
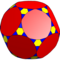
|
H(4;2;*;e) ttH |

|

| |||||
 |
7 | T(2;1;*;1) T(1;2;*;1) dM3T |

|
O(1;2;*;1) dM3O |

|
I(1;2;*;1) dM3I |

|
H(1;2;*;1) dM3Δ |

|

|
Q(2;1;*;1) Q(1;2;*;1) dM3dQ |

|

|
 |
7 | O(2;1;*;1) dM3C |

|
I(2;1;*;1) dM3D |

|
H(2;1;*;1) dM3H |

|

| |||||
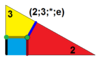 |
9 | T(2;3;*;e) T(3;2;*;e) dm3T |

|
O(2;3;*;e) dm3C |

|
I(2;3;*;e) dm3D |

|
H(2;3;*;e) dm3H |

|

|
Q(2;3;*;e) Q(3;2;*;e) dm3Q |

|

|
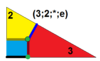 |
9 | O(3;2;*;e) dm3O |

|
I(3;2;*;e) dm3I |

|
H(3;2;*;e) dm3Δ |

|

| |||||
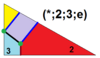 |
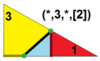
10 | T(2;*;3;e) T(*;2;3;e) dXdT 3.4.6.6 |

|
O(*;2;3;e) dXdO |

|
I(*;2;3;e) dXdI |

|
H(*;2;3;e) dXdΔ |

|

|
Q(2;*;3;e) Q(*;2;3;e) dXdQ |

|

|
 |
10 | O(2;*;3;e) dXdC 3.4.6.8 |

|
I(2;*;3;e) dXdD 3.4.6.10 |

|
H(2;*;3;e) dXdH |
|

| |||||
3-generator points[]
| Domain | Edges | Tetrahedral (3 3 2) | Octahedral (4 3 2) | Icosahedral (5 3 2) | Triangular (6 3 2) | Square (4 4 2) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symbol | Image | Symbol | Image | Symbol | Image | Symbol | Image | Dual | Symbol | Image | Dual | ||
 |
6 | T(2;0;*;[1]) | 
|
O(0;2;*;[1]) dL0dO |

|
I(0;2;*;[1]) dL0dI |

|
H(0;2;*;[1]) dL0H |

|

|
Q(2;0;*;[1]) Q(0;2;*;[1]) dL0dQ |
|

|
 |
6 | O(2;0;*;[1]) dL0dC |

|
I(2;0;*;[1]) dL0dD |

|
H(2;0;*;[1]) dL0Δ |

|

| |||||
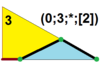 |
7 | T(3;0;*;[2]) | 
|
O(0;3;*;[2]) dLdO |

|
I(0;3;*;[2]) dLdI |

|
H(0;3;*;[2]) dLH |

|

|
Q(2;0;*;[1]) Q(0;2;*;[2]) dLQ |

|

|
 |
7 | O(3;0;*;[2]) dLdC |

|
I(3;0;*;[2]) dLdD |

|
H(3;0;*;[2]) dLΔ |

|

| |||||
 |
12 | T(2;2;*;a) amT |

|
O(2;2;*;a) amC |

|
I(2;2;*;a) amD |

|
H(2;2;*;a) amH |

|

|
Q(2;2;*;a) amQ |
|

|
See also[]
References[]
External links[]
- Symmetrohedra on RobertLovesPi.net.
- Antiprism Free software that includes Symmetro for generating and viewing these polyhedra with Kaplan-Hart notation.
- Polyhedra