Cantic 7-cube
| Truncated 7-demicube Cantic 7-cube | |
|---|---|
 D7 Coxeter plane projection | |
| Type | uniform 7-polytope |
| Schläfli symbol | t{3,34,1} h2{4,3,3,3,3,3} |
| Coxeter diagram | |
| 6-faces | 142 |
| 5-faces | 1428 |
| 4-faces | 5656 |
| Cells | 11760 |
| Faces | 13440 |
| Edges | 7392 |
| Vertices | 1344 |
| Vertex figure | ( )v{ }x{3,3,3} |
| Coxeter groups | D7, [34,1,1] |
| Properties | convex |
In seven-dimensional geometry, a cantic 7-cube or truncated 7-demicube as a uniform 7-polytope, being a truncation of the 7-demicube.
A uniform 7-polytope is vertex-transitive and constructed from uniform 6-polytope facets, and can be represented a coxeter diagram with ringed nodes representing active mirrors. A demihypercube is an alternation of a hypercube.
Its 3-dimensional analogue would be a truncated tetrahedron (truncated 3-demicube), and Coxeter diagram ![]()
![]()
![]() or
or ![]()
![]()
![]()
![]()
![]() as a cantic cube.
as a cantic cube.
Alternate names[]
- Truncated demihepteract
- Truncated hemihepteract (thesa) (Jonathan Bowers)[1]
Cartesian coordinates[]
The Cartesian coordinates for the 1344 vertices of a truncated 7-demicube centered at the origin and edge length 6√2 are coordinate permutations:
- (±1,±1,±3,±3,±3,±3,±3)
with an odd number of plus signs.
Images[]
It can be visualized as a 2-dimensional orthogonal projections, for example the a D7 Coxeter plane, containing 12-gonal symmetry. Most visualizations in symmetric projections will contain overlapping vertices, so the colors of the vertices are changed based on how many vertices are at each projective position, here shown with red color for no overlaps.
| Coxeter plane |
B7 | D7 | D6 |
|---|---|---|---|
| Graph | 
|

|
|
| Dihedral symmetry |
[14/2] | [12] | [10] |
| Coxeter plane | D5 | D4 | D3 |
| Graph | 
|
|
|
| Dihedral symmetry |
[8] | [6] | [4] |
| Coxeter plane |
A5 | A3 | |
| Graph | 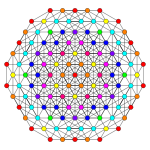
|

| |
| Dihedral symmetry |
[6] | [4] |
Related polytopes[]
| n | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|
| Symmetry [1+,4,3n-2] |
[1+,4,3] = [3,3] |
[1+,4,32] = [3,31,1] |
[1+,4,33] = [3,32,1] |
[1+,4,34] = [3,33,1] |
[1+,4,35] = [3,34,1] |
[1+,4,36] = [3,35,1] |
| Cantic figure |

|

|

|

|

|

|
| Coxeter | = |
= |
= |
= |
= |
= |
| Schläfli | h2{4,3} | h2{4,32} | h2{4,33} | h2{4,34} | h2{4,35} | h2{4,36} |
There are 95 uniform polytopes with D6 symmetry, 63 are shared by the B6 symmetry, and 32 are unique:
| D7 polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 t0(141) |
 t0,1(141) |
 t0,2(141) |
 t0,3(141) |
 t0,4(141) |
 t0,5(141) |
 t0,1,2(141) |
 t0,1,3(141) | ||||
 t0,1,4(141) |
 t0,1,5(141) |
 t0,2,3(141) |
 t0,2,4(141) |
 t0,2,5(141) |
 t0,3,4(141) |
 t0,3,5(141) |
 t0,4,5(141) | ||||
 t0,1,2,3(141) |
 t0,1,2,4(141) |
 t0,1,2,5(141) |
 t0,1,3,4(141) |
 t0,1,3,5(141) |
 t0,1,4,5(141) |
 t0,2,3,4(141) |
 t0,2,3,5(141) | ||||
 t0,2,4,5(141) |
 t0,3,4,5(141) |
 t0,1,2,3,4(141) |
 t0,1,2,3,5(141) |
 t0,1,2,4,5(141) |
 t0,1,3,4,5(141) |
 t0,2,3,4,5(141) |
 t0,1,2,3,4,5(141) | ||||
Notes[]
- ^ Klitzing, (x3x3o *b3o3o3o3o - thesa)
References[]
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
- Klitzing, Richard. "7D uniform polytopes (polyexa) x3x3o *b3o3o3o3o – thesa".
External links[]
- Weisstein, Eric W. "Hypercube". MathWorld.
- Polytopes of Various Dimensions
- Multi-dimensional Glossary
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform polychoron | Pentachoron | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
- 7-polytopes