Closed graph theorem

The graph of the cubic function ${\displaystyle f(x)=x^{3}-9x}$ on the interval ${\displaystyle [-4,4]}$ is closed because the function is continuous. The graph of the Heaviside function on ${\displaystyle [-2,2]}$ is not closed, because the function is not continuous.

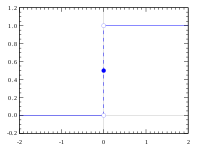
In mathematics, the closed graph theorem is a basic result which characterizes continuous functions in terms of their graphs. In particular, they give conditions when functions with closed graphs are necessarily continuous. In mathematics, there are several results known as the "closed graph theorem".

Graphs and maps with closed graphs[]

If ${\displaystyle f:X\to Y}$ is a map between topological spaces then the graph of ${\displaystyle f}$ is the set ${\displaystyle \operatorname {Gr} f:=\{(x,f(x)):x\in X\}}$ or equivalently,

$${\displaystyle \operatorname {Gr} f:=\{(x,y)\in X\times Y:y=f(x)\}}$$

the graph of ${\displaystyle f}$ is closed

${\displaystyle \operatorname {Gr} f}$

${\displaystyle X\times Y}$

Any continuous function into a Hausdorff space has a closed graph.

Any linear map, ${\displaystyle L:X\to Y,}$ between two topological vector spaces whose topologies are (Cauchy) complete with respect to translation invariant metrics, and if in addition (1a) ${\displaystyle L}$ is sequentially continuous in the sense of the product topology, then the map ${\displaystyle L}$ is continuous and its graph, Gr L, is necessarily closed. Conversely, if ${\displaystyle L}$ is such a linear map with, in place of (1a), the graph of ${\displaystyle L}$ is (1b) known to be closed in the Cartesian product space ${\displaystyle X\times Y}$, then ${\displaystyle L}$ is continuous and therefore necessarily sequentially continuous.^[1]

Examples of continuous maps that are not closed[]

If ${\displaystyle X}$ is any space then the identity map ${\displaystyle \operatorname {Id} :X\to X}$ is continuous but its graph, which is the diagonal ${\displaystyle \operatorname {Gr} \operatorname {Id} :=\{(x,x):x\in X\},}$, is closed in ${\displaystyle X\times X}$ if and only if ${\displaystyle X}$ is Hausdorff.^[2] In particular, if ${\displaystyle X}$ is not Hausdorff then ${\displaystyle \operatorname {Id} :X\to X}$ is continuous but not closed.

Let ${\displaystyle X}$ denote the real numbers ${\displaystyle \mathbb {R} }$ with the usual Euclidean topology and let ${\displaystyle Y}$ denote ${\displaystyle \mathbb {R} }$ with the indiscrete topology (where note that ${\displaystyle Y}$ is not Hausdorff and that every function valued in ${\displaystyle Y}$ is continuous). Let ${\displaystyle f:X\to Y}$ be defined by ${\displaystyle f(0)=1}$ and ${\displaystyle f(x)=0}$ for all ${\displaystyle x\neq 0}$. Then ${\displaystyle f:X\to Y}$ is continuous but its graph is not closed in ${\displaystyle X\times Y}$.^[3]

Closed graph theorem in point-set topology[]

In point-set topology, the closed graph theorem states the following:

For set-valued functions[]

In functional analysis[]

If ${\displaystyle T:X\to Y}$ is a linear operator between topological vector spaces (TVSs) then we say that ${\displaystyle T}$ is a closed operator if the graph of ${\displaystyle T}$ is closed in ${\displaystyle X\times Y}$ when ${\displaystyle X\times Y}$ is endowed with the product topology.

The closed graph theorem is an important result in functional analysis that guarantees that a closed linear operator is continuous under certain conditions. The original result has been generalized many times. A well known version of the closed graph theorems is the following.

See also[]

• Almost open linear map
• Banach space – Normed vector space that is complete
• Barrelled space – A topological vector space with near minimum requirements for the Banach–Steinhaus theorem to hold.
• Closed graph – Graph of a function that is also a closed subset of the product space
• Closed linear operator
• Continuous linear operator
• Discontinuous linear map
• Kakutani fixed-point theorem – On when a function f: S→Pow(S) on a compact nonempty convex subset S⊂ℝⁿ has a fixed point
• Locally convex topological vector space – A vector space with a topology defined by convex open sets
• Open mapping theorem (functional analysis) – Theorem giving conditions for a continuous linear map to be an open map
• Topological vector space – Vector space with a notion of nearness
• Ursescu theorem – Theorem that simultaneously generalizes the closed graph, open mapping, and Banach–Steinhaus theorems
• Webbed space – Topological vector spaces for which the open mapping and closed graphs theorems hold

Notes[]

References[]

Bibliography[]

• Bourbaki, Nicolas (1987) [1981]. Sur certains espaces vectoriels topologiques [Topological Vector Spaces: Chapters 1–5]. Annales de l'Institut Fourier. Éléments de mathématique. 2. Translated by Eggleston, H.G.; Madan, S. Berlin New York: Springer-Verlag. ISBN 978-3-540-42338-6. OCLC 17499190.
• Folland, Gerald B. (1984), Real Analysis: Modern Techniques and Their Applications (1st ed.), John Wiley & Sons, ISBN 978-0-471-80958-6
• Jarchow, Hans (1981). Locally convex spaces. Stuttgart: B.G. Teubner. ISBN 978-3-519-02224-4. OCLC 8210342.
• Köthe, Gottfried (1983) [1969]. Topological Vector Spaces I. Grundlehren der mathematischen Wissenschaften. 159. Translated by Garling, D.J.H. New York: Springer Science & Business Media. ISBN 978-3-642-64988-2. MR 0248498. OCLC 840293704.
• Munkres, James R. (2000). Topology (Second ed.). Upper Saddle River, NJ: Prentice Hall, Inc. ISBN 978-0-13-181629-9. OCLC 42683260.
• ; (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834.
• Rudin, Walter (1991). Functional Analysis. International Series in Pure and Applied Mathematics. 8 (Second ed.). New York, NY: McGraw-Hill Science/Engineering/Math. ISBN 978-0-07-054236-5. OCLC 21163277.
• Schaefer, Helmut H.; (1999). Topological Vector Spaces. GTM. 8 (Second ed.). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
• Trèves, François (2006) [1967]. Topological Vector Spaces, Distributions and Kernels. Mineola, N.Y.: Dover Publications. ISBN 978-0-486-45352-1. OCLC 853623322.
• Wilansky, Albert (2013). Modern Methods in Topological Vector Spaces. Mineola, New York: Dover Publications, Inc. ISBN 978-0-486-49353-4. OCLC 849801114.
• (30 July 2002). Convex Analysis in General Vector Spaces. River Edge, N.J. London: World Scientific Publishing. ISBN 978-981-4488-15-0. MR 1921556. OCLC 285163112 – via Internet Archive.
• "Proof of closed graph theorem". PlanetMath.